логарифм »
логарифмическое уравнение - страница 10
Решите логарифмическое уравнение a) \(\log_{\frac{1}{4}}(x^2+6x)=-2;\)
b) \(\log_2\frac{8}{x} -\log_2\sqrt{2x} =-0,5\)
Решение: А)
ОДЗ: x²+6x>0
x(x+6)>0
x=0 x= -6
+ - +
- -6 - 0 -
\\\\\\\\\ \\\\\\\\\\\\\
x∈(-∞; -6)U(0; +∞)
x²+6x=(1/4)⁻²
x²+6x=16
x²+6x-16=0
D=36+64=100
x₁=(-6-10)/2=-8
x₂=(-6+10)/2=2
Ответ; -8; 2.
б) ОДЗ:
1) 8/х >0
x>0
2) √(2x)>0
x>0
8/(x*√(2x))=2^(-0.5)
8/√(2x³)=1/√2
√(2x³)=8√2
2x³=64*2
x³=64
x³=4³
x=4
Ответ: 4Решите логарифмическое уравнение
Lg(7x-9)^2+lg(3x-4)^2=2
Решение: Lg(7x-9)²+lg(3x-4)²=2
7x-9>0⇒x>9/7;x>1.2857;
3x-4>0;⇒x>4/3;x>1.333
x>1.3333
2·lg(7x-9)+2·lg(3x-4)=2⇒2·[lg(7x-9)+lg(3x-4)]=2⇒
lg(7x-9)+lg(3x-4)=1;⇒
lg(7x-9)(3x-4)=lg10⇒
(7x-9)(3x-4)=10⇒ 21x²-27x-28x+36=10⇒
21x²-55x+26=0
x₁,₂=(55⁺₋√(55²-4·21·26))/42=(55⁺₋√841)/42=(55⁺₋29)/42;
x₁=(55+29)/42=2;x₁>1.3333
x₂=(55-29)/42=26/42=13/21=0.6191 не подходит, x₂<1.333
Решите логарифмическое уравнение. \(4\log_2(x+5) -\log_2(x+1)^4 =4 \)
Решение: Везде основание логарифма равно 2, поэтому писать его не буду.
4log(x+5)-log(x+1)^4=4;
4log(x+5)-4log(x+1)=4;
log(x+5)-log(x+1)=1;
log(x+5)-log(x+1)=1;
log((x+5)/(x+1))=1; теперь можно избавиться от логарифмов
(x+5)/(x+1)=2;
x+5=2x+2;
x=3; x<>-1; x<>-5;
Решите логарифмическое уравнение:
〖log〗_3(x+3)= 〖log〗_3(2x^2-4)- 〖log〗_3x
Решение: $$ \log_3(x+3)+\log_3x=\log (2x^2-4);\\ \left \{ \begin{array}{^} \log_3(x^2+3x)=\log_3(2x^2-4);\\ x>0; \end{array} \right.\\ \left \{ \begin{array}{^} x^2+3x=2x^2-4;\\ x>0;\\ 2x^2-4>0; \end{array} \right.\\ \left \{ \begin{array}{^} x^2-3x-4=0;\\ x>\sqrt2; \end{array} \right. $$
В последней системе из первого уравнения получаем два корня: (-1) и 4.1 не подходит из-за ограничения x>√2 (получается логарифм от отрицательного числа), 4 - подходит.
Ответ: 4.
Решите логарифмическое уравнение
\( log _{x^{3}-9 x^{2} +27x-27 } (9-x) \geq 0 \)
Решение:
log_(x-3)^3) (9-x) ≥ 0
1/3*log_(x-3) (9-x) ≥ 0 ; x∈(3;4) U ( 4;9) [x-3>0, x-3 ≠ 1, 9-x>0]
log_(x-3) (9-x) ≥ 0
log_(x-3) (9-x) ≥ log_(x-3) 1
выделяем два случая
a) x∈(3;4) [ 0< x< 1]
9-x ≤ 1
x ≥ 8, но учитывая, что x∈(3;4) == нет решения
b) x∈(4;9) х-3 > 1
9-x ≥ 1
x ≤ 8, но учитывая, что x∈(4;9) получим x ∈(4;8]
ответ : x ∈(4;8]



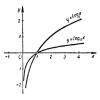 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...