логарифм »
логарифмическое неравенство - страница 5
Логарифмическое неравенство \(\sqrt{ log_{9}(3x^2-4x+2)} > log_{3}(3x^2-4x+2) -1 \)
Решение: Сразу напрашивается замена $$ log_{3}(3x^2-4x+2)=t $$. Тогда
$$ \sqrt{ \frac{1}{2} t} \ > \ t-1 $$
Если t<1 неравенство выполняется при любом t≥0. Значит часть решения выглядит так: 0≤t<1
Если t≥1 мы имеем право возвести обе части в квадрат:
$$ \frac{1}{2}t\ > \ t^2-2t+1 \\ 2t^2-5t+2\ < \ 0 \\ \frac{1}{2} \ < \ t\ < \ 2 $$
Объединим оба полученных промежутка и получим 0≤t<2. Возвращаемся к замене:
$$ 0 \leq log_{3}(3x^2-4x+2)\ < \ 2 \\ log_31\ \leq log_{3}(3x^2-4x+2)\ < \ log_39 \\ 1\ \leq 3x^2-4x+2\ < \ 9 $$
Решаем и получаем ответ: (-1; 1/3] U [1; 7/3)
Логарифмическое неравенство: \(\frac{\log_2(3\cdot 2^{x-1} -1)}{x}\geq 0\)
Решение: Найдем область определения дроби в левой части. Знаменатель определен при $$ xeq 0 $$, числитель определен, если
$$ 3\cdot 2^{x-1}-1> 0 \\ 3\cdot 2^{x-1}> 1 \\ 2^{x-1} > \frac{1}{3} \\ x-1 > log_2(\frac{1}{3}) \\ x > log_2(\frac{1}{3})+1 $$
Заметим, что $$ log_2(\frac{1}{3})+1=-log_2(3)+1<0 $$
Таким образом, область определения дроби
$$ (log_2(\frac{1}{3})+1;0)\cup(0;+\infty) $$
Найдем значения аргумента, при которых числитель неотрицателен:
$$ log_2(3\cdot 2^{x-1}-1)\geq 0 \\ 3\cdot 2^{x-1}-1\geq 1 \\ 3\cdot 2^{x-1}\geq 2 \\ 2^{x-1} \geq \frac{2}{3} \\ x-1 \geq log_2(\frac{2}{3}) \\ x \geq log_2(\frac{2}{3})+1 \\ log_2(\frac{2}{3})+1=log_2(2)-log_2(3)+1=2-log_2(3)>0. $$
Таким образом, на интервале $$ (log_2(\frac{1}{3})+1;0) $$ и числитель и знаменатель принимают отрицательные значения, поэтому дробь принимает положительные значения и все точки этого интервала нам подойдут.
На интервале $$ (0;log_2(\frac{2}{3})+1)) $$ числитель принимает отрицательные значения, а знаменатель принимает положительные значения, поэтому дробь принимает отрицательные значения.
На луче $$ [log_2(\frac{2}{3})+1;+\infty) $$ числитель принимает неотрицательные значения, знаменатель принимает положительные значения, поэтому дробь принимает неотрицательные значения и все точки этого луча нам подойдут.
Ответ: $$ (log_2(\frac{1}{3})+1;0)\cup[log_2(\frac{2}{3})+1;+\infty). $$Логарифмическое неравенство \(\log_2(\log_{\frac{1}{3}}\log_5 x) > 0\)
Решение: $$ log_2(log_{\frac{1}{3}}log_5x)\ > \ 0\\\\ODZ:\; \; \left \{ {{x\ > \ 0,\; log_5x\ > \ 0} \atop {log_{\frac{1}{3}}(log_5x)\ > \ 0}} \right. \; \left \{ {{x\ > \ 0,\; x\ > \ 1} \atop {0\ < \ log_5x\ < \ 1}} \right. \; \left \{ {{x\ > \ 1} \atop {1\ < \ x\ < \ 5}} \right. \; \; \Rightarrow \; \; 1\ < \ x\ < \ 5\\\\log_{\frac{1}{3}}(log_5x)\ > \ 1\; \; \Rightarrow \; \; 0\ < \ log_5x\ < \ \frac{1}{3}\; \; \Rightarrow \; \; 1\ < \ x\ < \ \sqrt[3]5\\\\Otvet:\; \; x\in (1,\sqrt[3]5)\\ $$Логарифмическое неравенство \(log_{\frac{1}{6}} (3x-4) > -1\)
Решение: $$ log_{\frac{1}{6}} (3x-4) > -1 $$
ОДЗ: $$ 3x-4>0 \\ x>\frac{4}{3} \\ 0<\frac{1}{6}<1 \\ 3x-4< (\frac{1}{6})^{-1} \\ 3x-4<6 \\ 3x<6+4 \\ 3x<10 \\ x<\frac{10}{3} $$
итого
$$ \frac{4}{3} < x < \frac{10}{3} \\ х є (\frac{4}{3};\frac{10}{3}) $$Логарифмическое неравенство \(log_3(2-3^x) < x+1-log_34\)
Решение: $$ log_3(2-3^x)\ < x+1-log_34 \\ \\ log_3(2-3^x)+log_34\ < \ (x+1)\cdot log_33 \\ \\ log_3(2-3^x)\cdot 4\ < \ log_33^{x+1} \\ \\ \left \{ {{2-3^x\ > \ 0} \atop {(2-3^x)\cdot 4 \ < \ 3^{x+1} }} \right. \\ \left \{ {{2-3^x\ > \ 0} \atop {8-4\cdot 3^x \ < \ 3\cdot3^{x} }} \right. \\ \\ \left \{ {{3^x\ < \ 2} \atop {8\ < \ 7\cdot3^{x} }} \right. \\ \\ \frac{8}{7}\ < \ 3^x\ < \ 2 \\ \\ log_3{ \frac{8}{7}}\ < \ x\ < \ log_32 $$

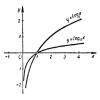 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...