логарифмически
Решить логарифмические системы:
1) \( \left \{ {{ x^{2} + y^{2} =5} \atop { log_{2}x+ log_{2} y=1 }} \right. \)
2) \( \left \{ {{ x^{2} - y^{2}=12 } \atop { log_{2}x- log_{2}y=1 }} \right. \)
3) \( \left \{ {{ x^{2} + y^{2}=25 } \atop { lgx+lgy=lg12}} \right. \)
4) \( \left \{ {{ log_{0,5} + log_{0,5}=-1 } \atop {x-2y=3}} \right. \)
Решение: 1
x>0,y>0
{x²+y²=5
{log(2)x+log(2)y=1⇒log(2)xy=1⇒xy=2⇒2xy=4
прибавим
x²+y²+2xy=9
(x+y)²=9
a)x+y=-3
x=-3-y
-3y-y²=2
y²+3y+2=0
y1+y2=-3 U y1*y2=2
y1=-2 не удов усл
у2=-1 не удов усл
б)x+y=3
x=3-y
3y-y²=2
y²-3y+2=0
y1+y2=3 U y1*y2=1
y1=1⇒x1=2
y2=2⇒x2=1
(2;1);(1;2)
2
x>0,y>0
{x²-y²=12
log(2)x-log(2)y1⇒log(2)(x/y)=1⇒x/y=2⇒x=2y
4y²-y²=12
3y²=12
y²=4
y1=-2 не удов усл
y2=2⇒x=4
(4;2)
3
x>0,y>0
{x²+y²=25
lgx+lgy=lg12⇒xy=12⇒2xy=24
x²+y²+2xy=49
(x+y)²=49
a)x+y=-7
x=-y-7
-y²-7y=12
y²+7y+12=0
y1+y2=-7 U y1*y2=12
y1=-3 не удов усл
y2=-4 не удов усл
б)x+y=7
x=7-y
7y-y²=12
y²-7y+12=0
y1+y2=7 U y1*y2=12
y1=3⇒x1=4
y2=4⇒x2=3
(4;3);(3;4)
4
x>0 y>0
{log(0,5)xy=-1⇒xy=2
{x=3+2y
3y+2y²-2=0
D=9+16=25
y1=(-3-5)/4=-2 не удов усл
у2=(-3+5)/4=0,5⇒х=4
(4;0,5)
X²+y²=5 (2/y)²+y²=5 4+y⁴=5y² y⁴-5y²+4=0
log₂x+log₂y=1 log₂xy=log₂2 xy=2 x=2/y
y²=t ⇒
t²-5t+4=0 D=9
t₁=1 y₁=1 x₁=2 y₂=-1 x₂=-2
t₂=4 y₃=2 x₃=1 y₄=-2 x₄=-1.
Остальные системы решаются аналогично.
Решить логарифм: \( \log_7(4x^2-18x+13) - \log_7(2x-8)=0 \)
Решение: log7 (4x^2 - 18x + 13) - log7 (2x - 8) = 0;log7 (4x^2 - 18x + 13) = log7 (2x - 8);
т. к. логарифмы по одному основанию, то их можно убрать.
4x^2 - 18x + 13 = 2x - 8;
4x^2 - 20x + 21 = 8;
Решаем как обычное квадратное.
x1 = 1.5, x2 = 3.5
Ответ B
Первое, что нужно делать - искать область допустимых значений (ОДЗ):
$$ \left \{ {{4x^2-18x+13\ > \ 0} \atop {2x-8\ > \ 0}} \right.; $$, первое неравенство квадратное, решаем методом интервалов с первоначальным разложением квадратного трёхчлена, находя его корни: $$ 4x^2-18x+13=0; D_1=9^2-4*13=29; x= \frac{9б \sqrt{29} }{4}; $$, $$ 4(x- \frac{9- \sqrt{29} }{4})(x- \frac{9+ \sqrt{29} }{4})\ > \ 0; \\ x\ > \ \frac{9+ \sqrt{29} }{4}; x\ < \ \frac{9- \sqrt{29} }{4}; $$. Из второго неравенства системы следует, что x > 4, то есть первый промежуток отбрасываем 100%, $$ \frac{9+ \sqrt{29} }{4}\ < 4; $$, из этого следует, что x>4 по ОДЗ.
Теперь решаем само уравнение: $$ log_7(4x^2-18x+13)=log_7(2x-8); 4x^2-18x+13=2x-8; \\ 4x^2-20x+21=0; D_1=10^2-4*21=16=4^2; x= \frac{10б4}{4}; \\ x=1,5; x=3,5 $$, оба решения не соответствуют ОДЗ, поэтому правильный ответ, где нет корнейКак сравнить логарифмические функции по их свойствам?
log2(5) и log2(3)?
Решение: Решим сперва данный пример:
$$ log_25 $$ и $$ log_23 $$
т. к. у логарифмов основание одинаковое, то мы имеем право опустить логарифм и сравнивать уже по его числу
5 и 3
следовательно. $$ log_25>log_23 $$
теперь рассмотрим более сложный пример
$$ log_{\frac{1}{5}}\frac{10\sqrt{5}}{\sqrt{3}} $$ и $$ -(log_{25}4+log_{25}120-log_{25}3) \\ -log_5\frac{10\sqrt{5}}{\sqrt{3}} $$ и $$ -\frac{1}{2}(log_{5}4+log_{5}120-log_{5}3) $$
умножим обе части на -2 и надо бы не забыть поменять в этом месте знак неравенства.
$$ 2log_{5}\frac{10\sqrt{5}}{\sqrt{3}} $$ и $$ log_{5}(4*120)-log_{5}3) \\ log_{5}\frac{100*5}{3} $$ и $$ log_{5}(480)-log_{5}3) \\ log_{5}(100*5)-log_5(3) $$ и $$ log_{5}(480)-log_{5}3) $$
прибавим к обеим частям $$ log_53 \\ log_{5}(100*5) $$ и $$ log_{5}(480) $$
т. к. у логарифмов одинаковое основание, то их можно опустить
500 и 480
отсюда видно, что 500 > 400, следовательно.
$$ log_{\frac{1}{5}}\frac{10\sqrt{5}}{\sqrt{3}} < -(log_{25}4+log_{25}120-log_{25}3) $$
PS меньше, потому что мы, в ходе решения, поменяли знак (когда умножили на -2)
Преобразование логарифмических выражений. Вычислить: \(100^{\lg\sqrt5}\); \(\log_{64}\frac{1}{16}\); \(10^{2-3\lg5}\)
Прологарифмировать выражение \(x=\frac{a^7}{c^3}\)
Найти x, если \(\lg x =2\lg3+3\lg2\)
Решение: 1. 1) $$ 100^{lg \sqrt{5} } =10 ^{lg \sqrt{5}}*10^{lg \sqrt{5}}= \sqrt{5} ^{lg10}*\sqrt{5} ^{lg10}=\sqrt{5}* \sqrt{5} = \sqrt{5} ^{2} = 5 $$
2) $$ log _{64} \frac{1}{16} $$ то есть 64 нам нужно возвести в степень x чтобы получилась $$ \frac{1}{16} $$ можем составить из этого уравнение, если ответ для тебя не очевиден.
$$ 64^{x} = \frac{1}{16} $$ представим в виде степеней двойки
$$ 2 ^{6x} =2 ^{-4} $$ теперь мы можем снести
$$ 6x=-4 $$ ⇒ $$ x=- \frac{2}{3} $$
3) $$ 10^{2 - 3 lg5} $$ это тоже самое, что и $$ \frac{ 10^{2} }{ 10^{3lg5}} $$ = $$ \frac{100}{ 5^{3} } = \frac{100}{125} = 0.8 $$
2. $$ x = 7* lg (a) - 3 *lg (c) $$
3. lgx= 2lg3+3lg2
$$ lgx = lg 3^{2} + lg 2^{3} $$
$$ lg x = lg 9 + lg8 $$
по свойству мы можем умножить, если показатели одинаковые
$$ lg x = lg 72 $$⇒ x= 72Решения логарифмических неравенств
Log1/2X<Log1/2(2X+6)+2
Решение: 1. одз: 1) х˃02) 2х+6˃0; х˃-3
значит х принадлежит промежутку (0;+).
2. заменим 2 на log1/2(1/2)^2, тогда неравенство примет вид
log 1/2x< log1/2(2x+6)+log1/2(1/2)^2,
log1/2x< log1/2(2x+6)+log1/2(1/4),
log 1/2x< log1/2[(2х+6)·(1/4)],
так как основания log равны влевой и вправой части и 1/2 <1, то знак неравенство меняется на противоположный
х˃(2х+6)·(1/4), раскроем скобки в левой части
х˃1/2х+3/2,
х-1/2х˃3/2,
1/2х˃3/2,
х˃3, хϵ(3;+∞)
Так как в одз хϵ(0;+∞), то общее решение хϵ(3;+∞)
Ответ: хϵ(3;+∞)

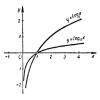 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...