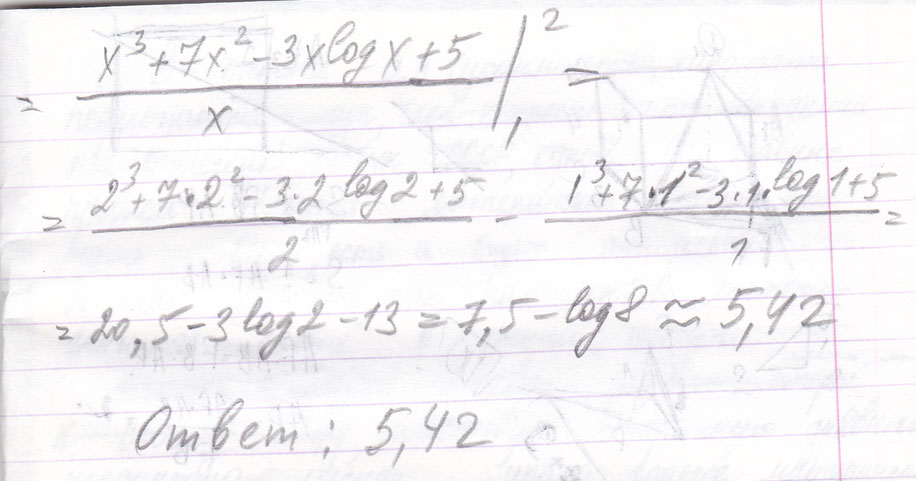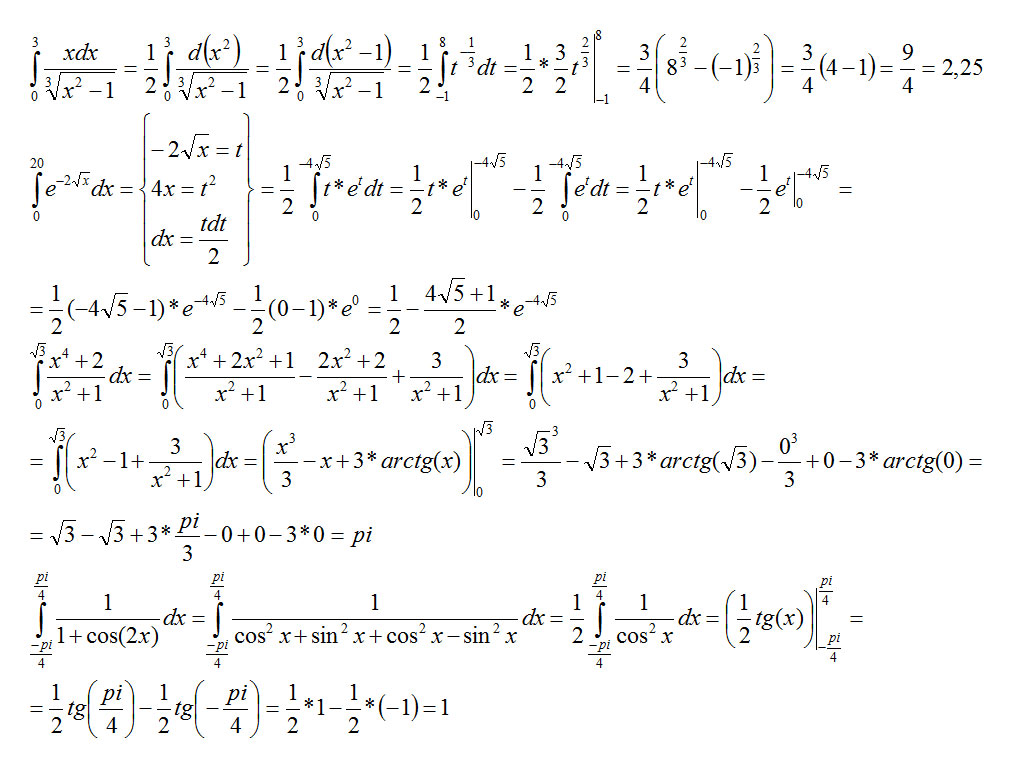вычислить определенный интеграл - страница 2
Вычислите определенный интеграл: Интеграл от 2 до 1 (2x^3+7x^2-3x-5)/x^2 dx
Решение: Интеграл от 2 до 1 (2x^3+7x^2-3x-5)/x^2 dxНайдем первообразную и вычислим на заданном интервале
Интеграл от 2 до 1 $$ 2 до 1 (2x^3+7x^2-3x-5):x^2 dx $$
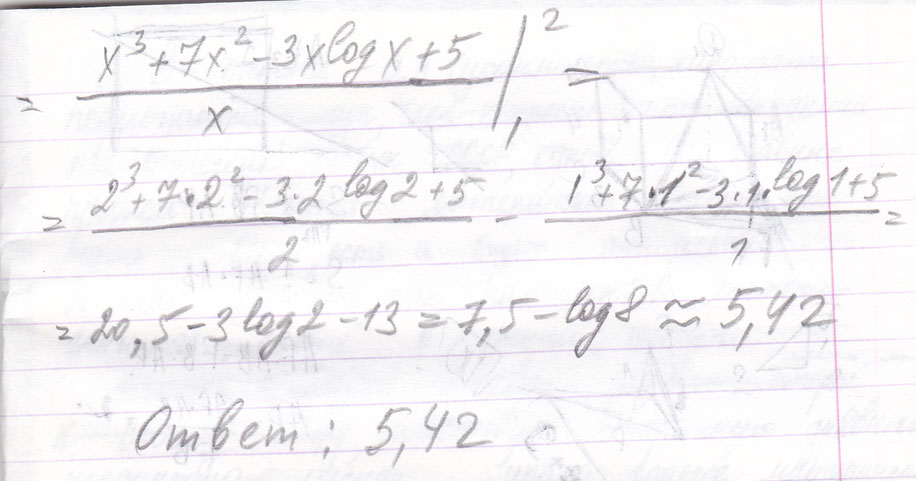
Вычислить определенный интеграл от функции e^cx cosωx на отрезке [a,b], где a=[π/ω, b=π/2ω].
c=4; ω=7
Решение: Интеграл берется двукратным последовательным интегрированием по частям. 1-раз u(x)=e^cx; dv=(cosωx)dx;2-й раз u1(x)=(c/ω)*e^cx;dv=(sinωx)dx;
с последующим упрощением выражения ( приведение подобных членов).
Определенный интеграл вычисляется из неопределенного путем вычитания
его значения при нижней границе из значения при верхней границе интегрирования.
Ответ в общем виде таков:
$$ \frac{\omega}{(c^2)+(\omega^2)}*e^{\pi*c/2*\omega}+\frac{c}{(c^2)+(\omega^2)}*e^{\pi*c/\omega} $$
После подстановки конкретных значений "с" и "омега", имеем:
(4/65)* e^((4/7)*pi)+(7/65)*e^((2/7)*pi) = 0,63475
Пока займемся вычислением неопр. интеграла:
I = $$ \int{e^{cx}coswx}\, dx\ =\ \frac{1}{c}\int{coswx}\, de^{cx}\ =\ \frac{1}{c}e^{cx}coswx\ +\ \frac{w}{c}\int{e^{cx}sinwx}\, dx\ =\\\ =\ \frac{1}{c}e^{cx}coswx\ -\ \frac{w}{c^2}\int{sinwx}\, de^{cx}\ = \\ =\ \frac{1}{c}e^{cx}coswx\ +\ \frac{w}{c^2}e^{cx}sinwx\ -\ \frac{w^2}{c^2}*\ I $$
Отсюда находим I:
$$ I\ =\ \frac{e^{cx}(c*coswx+w*sinwx)}{c^2+w^2} $$
Подставив значения с и w:
$$ I\ =\ \frac{e^{4x}(4cos7x+7sin7x)}{65} $$
Теперь найдем значение интеграла от П/w до П/2w:
$$ I\ =\ \frac{e^{2\pi/7}(7+4e^{2\pi/7})}{65} $$
1) Вычислить определенные интегралы a)\( \int\limits_0^{\sqrt3}\frac{x^4+2}{1+x^2}dx \)
б) \( \int\limits_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\frac{dx}{1+cos2x}, \, t=tgx\)
2) Вычислить несобственные интегралы или установить их расходимость а) \(\int\limits_0^{20}e^{-2\sqrt x}dx \)
б) \(\int\limits_0^3\frac{xdx}{\sqrt[3]{x^2-1}} \)
Решение: 1
a)(x^4+1)/(x²+1)=(x²+1)²/(x²+1) -2(x²+1)/(x²+1)+3/(x²+1)=(x²+1)-2+3/(x²+1)=
(x²-1)+3/(x²+1)
$$ \int\limits {(x^2-1)} \, dx +3 \int\limits {1/(x^2+1)} \, dx =x^3/3-x+3arctgx $$=
=3√3/3-√3+3*π/3-0+0-0=√3-√3+π=π
b)1/(1+cos2x)=1/2cos²x
$$ \int\limits {1/2cos^2x} \, dx =tgx/2=1/2*(1+1)=1 $$
2
a)=-e^-2√x(2√x+1)=-e^-2√5
b)=3/2*∛(x²-1)=3/2*∛8-3/2*∛-1=3/2*2-3/2*(-1)=3+1,5=4,5Смотри решение во вложении
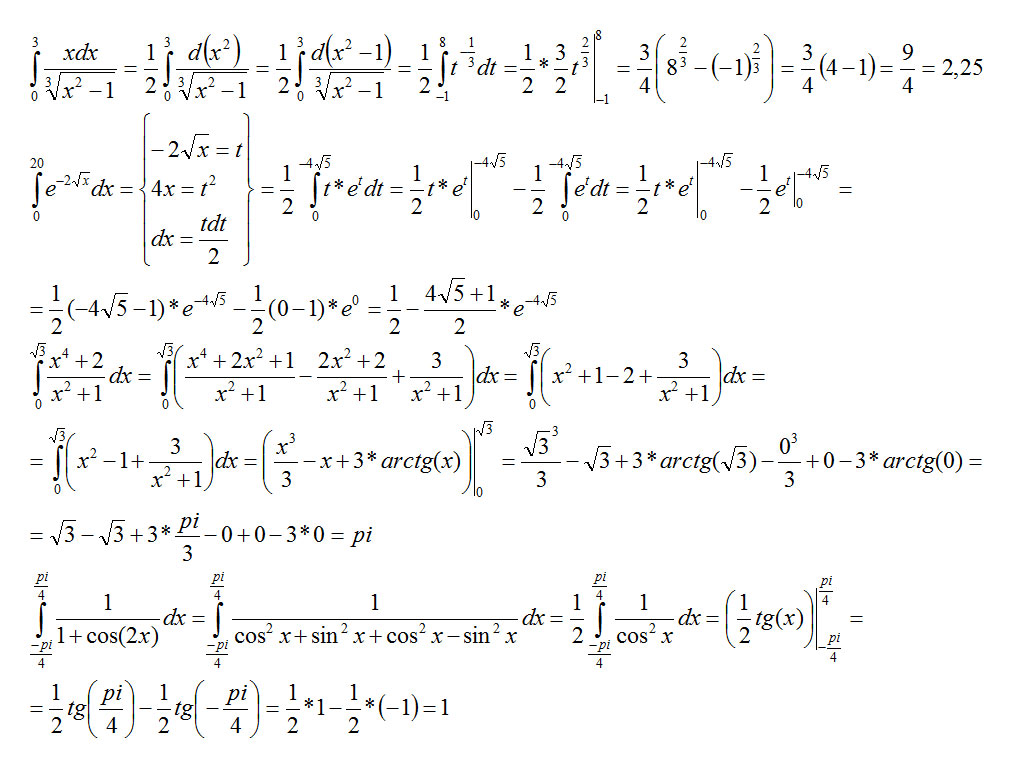
Геометрический смысл определенного интеграла.
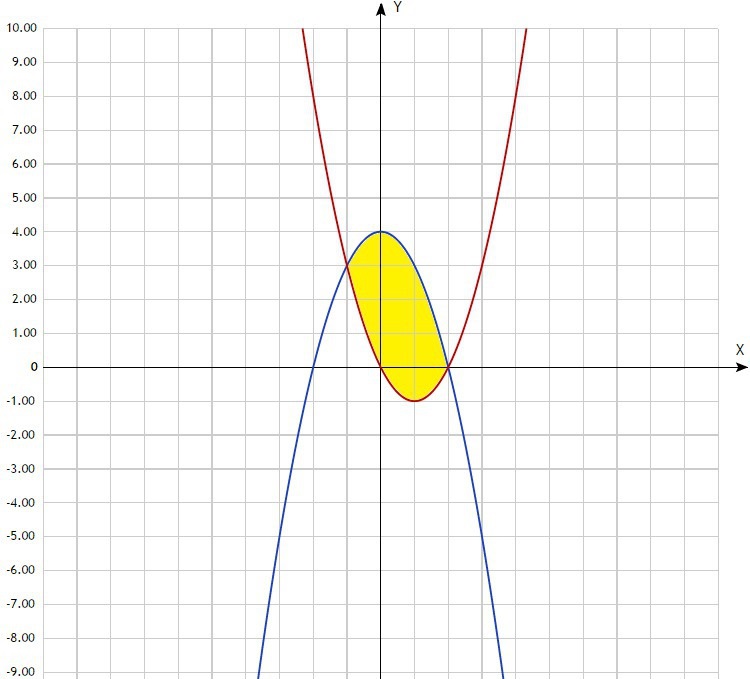
Вычислить площадь фигуры, ограниченной линиями
y = 4 – x2, y = x2 – 2x
Решение: Делаем чертёж. По нему определяем пределы интегрирования [-1;2]. График функции y=4-x² на промежутке [-1;2] выше графика функции y=x²-2x, значит вычисление площади фигуры будет проходить по формуле:
$$ s= \int\limits^2_{-1} {(4-x^2-x^2+2x)} \, dx= \int\limits^2_{-1} {(-2x^2+2x+4)} \, dx= \\ =(- \frac{2x^3}{3}+x^2+4x)|_{-1}^2= \\ - \frac{2*2^3}{3}+2^2+4*2-(- \frac{(-1)^3}{3}+(-1)^2+4*(-1 ))= \\ =- \frac{16}{3}+4+8- \frac{1}{3}-1+4= -\frac{20}{3}+16=9 \frac{1}{3} $$ ед².
Пользуясь геометрическим смыслом определённого интеграла, вычислите:
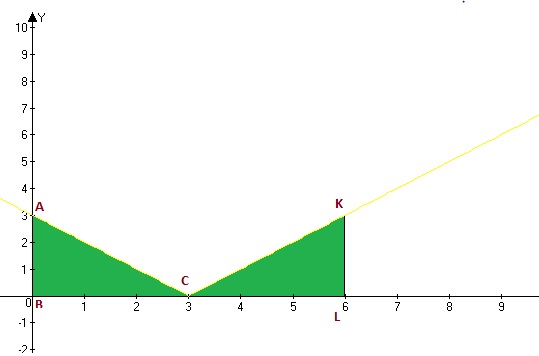
\( \int\limits^6_0 {|x-3|} \, dx \)
Решение: Построим график функции f(x)=|x-3|
План построения графика:
1) Строим f(x)=x-3, прямую проходящую через точки (0;-3), (3;0)
2) Нижнюю часть графика f(x)=x-3, отобразить относительно оси Ох и получим график функции f(x)=|x-3|
На графике отметим ограченные линии [0;6]. Видим что они образуют прямоугольные треугольники с катетами 3.
Площадь фигуры ограниченными линиями будет сумма площадей прямоугольных треугольников.
Назовём первый треугольник ARC, а другой - KLC
Площадь ARC = AR*RC = 3*3 = 9 кв. ед.
Площадь KLC = KL * LC = 3*3 = 9 кв. ед.
Площадь ограниченной фигуры: S=S₁+S₂=9+9 = 18 кв. ед.
Ответ: 18.