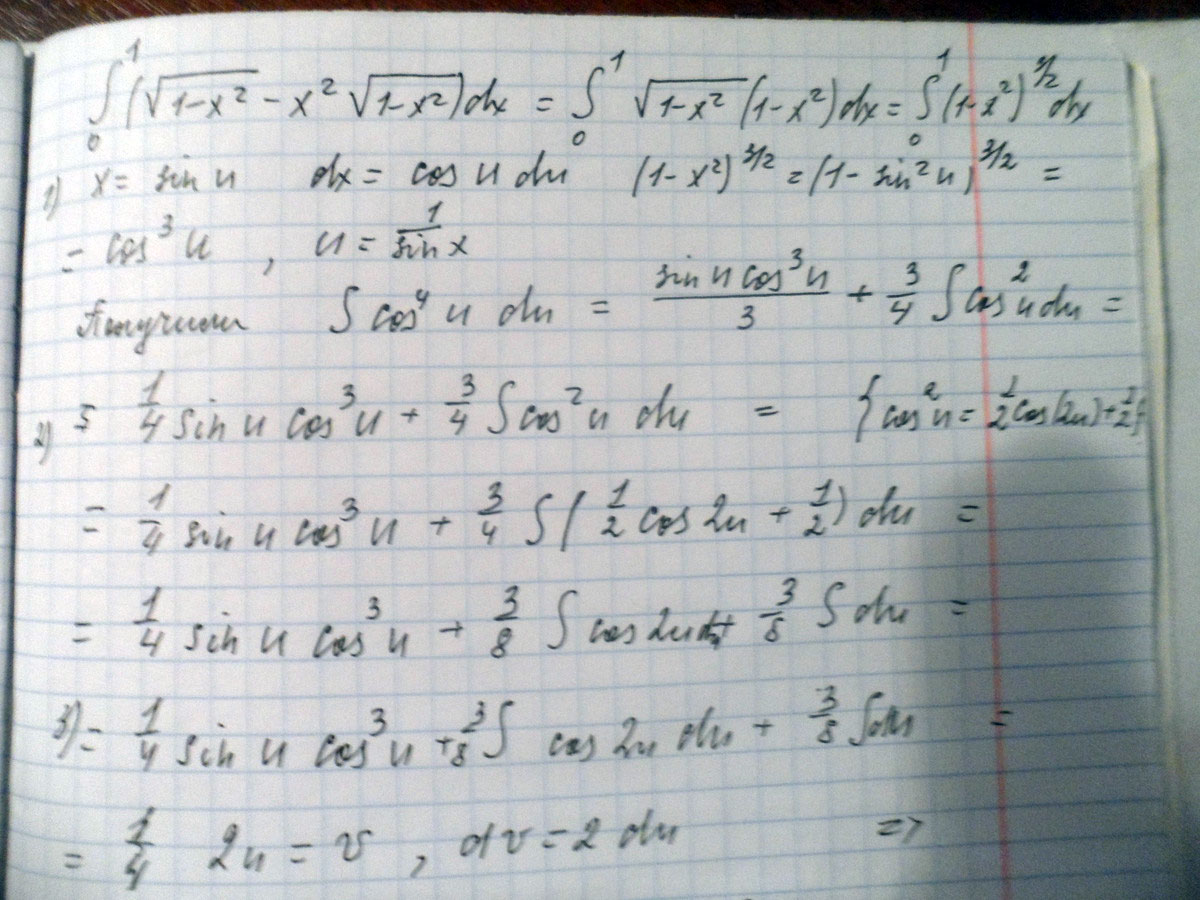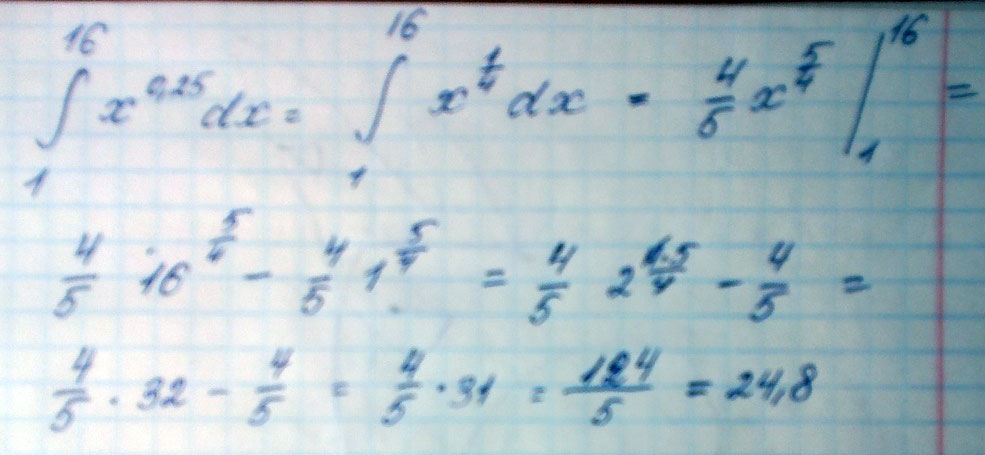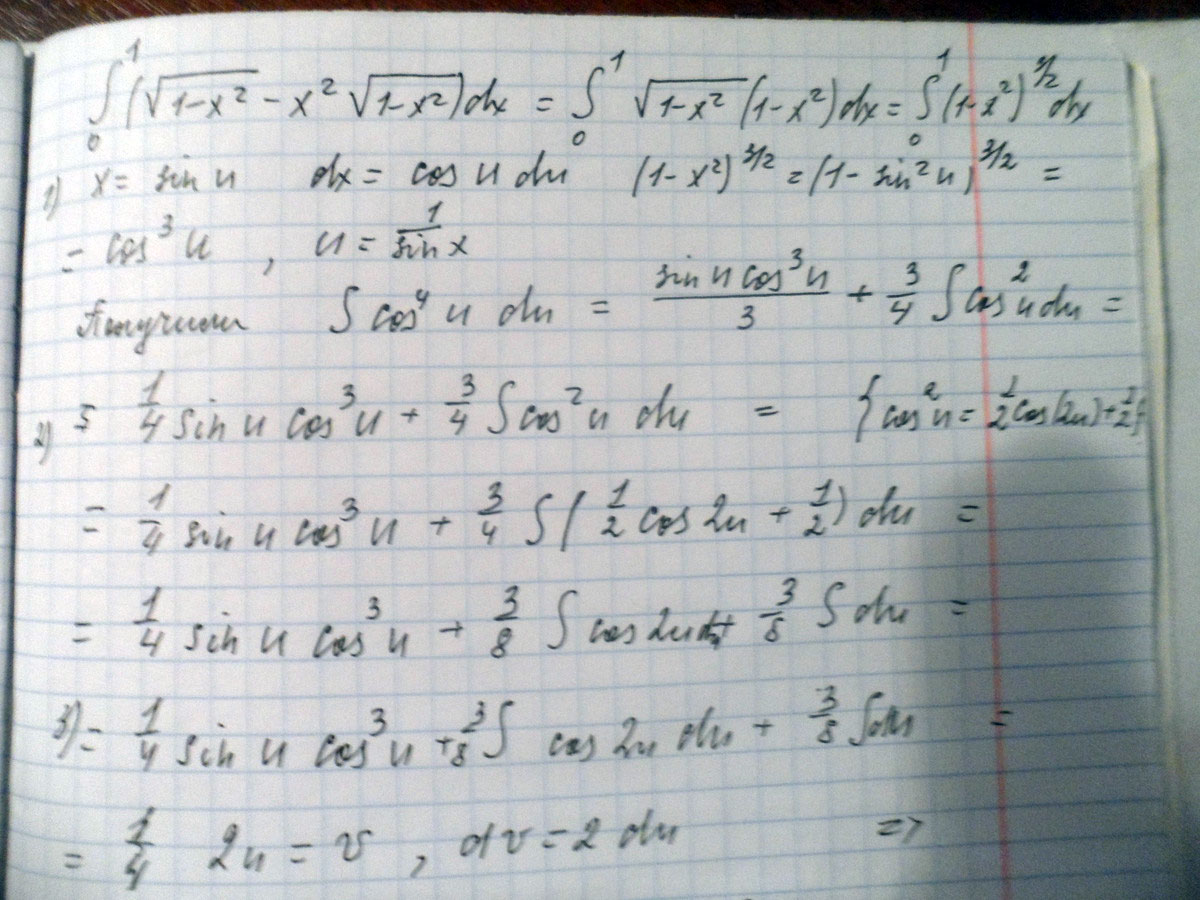вычислить определенный интеграл - страница 3
1 Вычислите определённый интеграл.
1. ∫_1^(e^4)*√xlnx dx интеграл от 1 до е в четвертой степени
Решение: $$ \int\limits^{e ^{4}} _1 { \sqrt{x} lnx} \, dx=[u=lnx \Rightarrow du= \frac{1}{x}dx||dv= \sqrt{x} dx\Rightarrow v= \frac{x ^{ \frac{3}{2} } }{ \frac{3}{2} } ]= \\ = \frac{2}{3}x ^{ \frac{3}{2} } \cdot lnx|_1^{e ^{4}}- \int\limits^{e ^{4}} _1 { \frac{2}{3}x ^{ \frac{3}{2} }\cdot \frac{1}{x} } \, dx = \\ \frac{2}{3}x \sqrt{x} \cdot lnx|_1^{e ^{4}}-\frac{2}{3} \int\limits^{e ^{4}} _1 { \sqrt{x} } \, dx = \\ =\frac{2}{3}x \sqrt{x} \cdot lnx|_1^{e ^{4}}-\frac{2}{3} \cdot \frac{2}{3}( x \sqrt{x} )|^{e ^{4}} _1 = \\ = \frac{20}{9}e ^{5} \sqrt{e}+ \frac{4}{9} $$
, нужно вычислить определенный интеграл от П/2 до П
dx
_______________
sin^2(x/2)cos^2(x/2)
Решение: $$ \int\limits^ \frac{ \pi }{} _ \frac{\pi}{2} \frac{1}{ \frac{1-cosx}{2} *\frac{1+cosx}{2}} \, dx =\int\limits^ \frac{ \pi }{} _ \frac{\pi}{2} \frac{4}{ ({1-cos ^{2} x} )} \, dx = \int\limits^ \frac{ \pi }{} _ \frac{\pi}{2} \frac{4}{ ({sin ^{2} x} )} \, dx=4*\int\limits^ \frac{ \pi }{} _ \frac{\pi}{2} \, d(-ctgx) $$
И тут мы явно видим, что этот интеграл является несобственным интегралом.
Будем решать дальше с пределом на Пи и установлением факта расходимости данного интеграла?
Вычислить по формуле Ньютона-Лейбница определенный интеграл.
\( \int\limits^4_1 {\frac{e^{\sqrt{x}}}{\sqrt{x}}} \, dx \)
Решение: Ну для начала возьмем все таки этот интеграл (сначала можно как неопределенный)$$ \int{\frac{e^\sqrt(x)}{\sqrt(x)}}\, dx= $$ {сделаем замену $$ u=\sqrt{x}, du=\frac{1}{2\sqrt{x}}dx $$ } продолжаем вычисление $$ =2\int{e^u}\, du=2e^u+C $$
Теперь вернемся к исходным переменным: $$ 2e^u=2e^{\sqrt{x}} $$
Интеграл взяли, теперь вспоминаем формулу Ньютона-Лейбница: $$ \int\limits^a_b {f(x)} \, dx=F(b)-F(a) $$, где F(x)-какая-либо первообразная от функции f(x). Выше мы нашли первообразную от f(x) и она оказалась равна F$$ F(x)=2e^{\sqrt{x}} $$, константу здесь сделали 0.
Ну и теперь получаем
$$ \int\limits^4_1{\frac{e^\sqrt(x)}{\sqrt(x)}}\, dx=2(e^2-e) $$
Ответ: $$ \int\limits^4_1{\frac{e^\sqrt(x)}{\sqrt(x)}}\, dx=2(e^2-e) $$
Примечание: почему сначала брали неопределенный интеграл? Потому что при любой замене в определенном интеграле необходимо пересчитывать пределы интегрирования. Но поскольку мы пользуемся формулой Ньютона-Лейбница, в которой нам нужно найти именно первообразную, то можно воспользоваться и неопределенным интегралом, чтобы ничего не пересчитывать.
Вычислите определённый интеграл от1 до 16 x^0,25 dx
Решение: Integral iz funkcii xˇ0,25 = 0,8.xˇ1,25.
0,8.(16ˇ1,25-1ˇ1,25)=0,8.(2ˇ5-1)=0,8.(32-1)=0,8.31=24,8
. Использована формула интеграл степенной функции
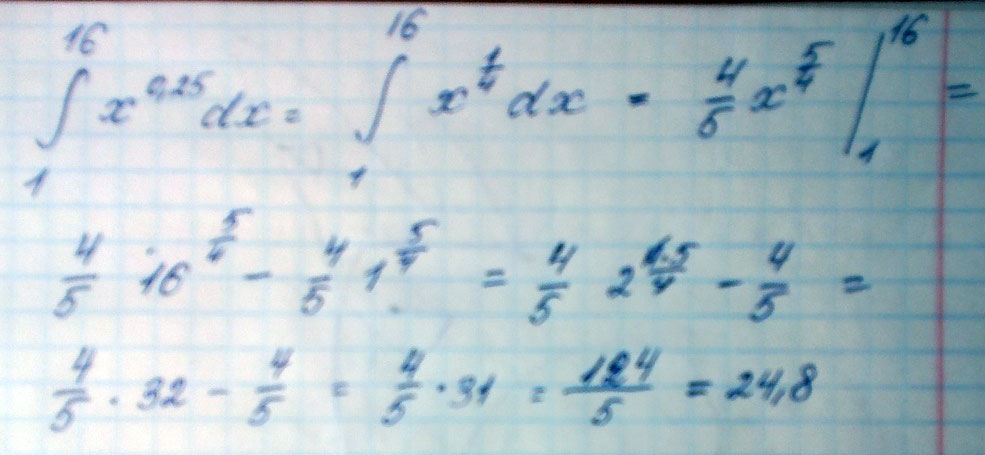
Вычислить определенный интеграл. ( сделать замену x=sinx) \( \int\limits^1_0 { \sqrt{1- x^{2} } - x^{2} \sqrt{1- x^{2} } } \, dx \)
Решение: $$ \int _0^1(\sqrt{1-x^2}-x^2\sqrt{1-x^2})dx=\\\\=[\, x=sint,dx=cost\cdot dt,t=arcsinx,\\t_1=arcsin0=0,t_2=arcsin1=\frac{\pi}{2}\, ]=\\\\=\int _0^{\frac{\pi}{2}}(\sqrt{1-sin^2t}-sin^2t\sqrt{1-sin^2t})\cdot cost\cdot dt=\\\\=\int _0^{\frac{\pi}{2}}(\sqrt{cos^2t}-sin^2t\sqrt{cos^2t})\cdot cost\cdot dt=\\\\=\int_0^{\frac{\pi}{2}}cos^2t\cdot dt-\int _0^{\frac{\pi}{2}}sin^2t\cdot cos^2t\cdot dt=\\\\=\int_0^{\frac{\pi}{2}}\frac{1+cos2t}{2}dt-\int _0^{\frac{\pi}{2}}\frac{1}{4}sin^22t\cdot dt= \\ =(\frac{1}{2}t+\frac{1}{4}sin2t)|_0^{\frac{\pi}{2}}-\frac{1}{4}\int _0^{\frac{\pi}{2}}\frac{1-cos4t}{2}dt=\\\\=\frac{\pi}{4}-\frac{1}{8}(t-\frac{1}{4}sin4t)|_0^{\frac{\pi}{2}}=\frac{\pi}{4}-\frac{1}{8}(\frac{\pi}{2}-0)=\frac{3\pi}{16} $$