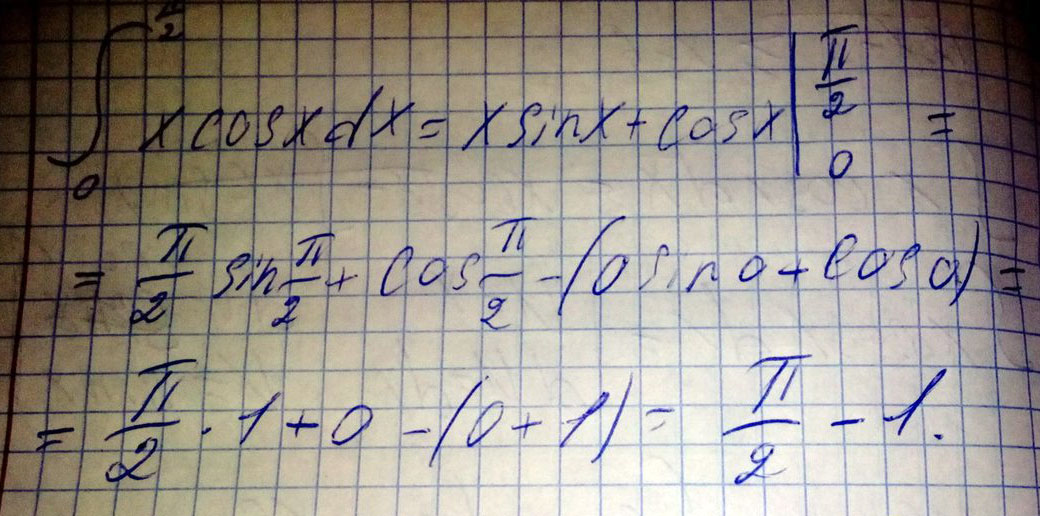интеграл »

вычислить определенный интеграл - страница 5

  • Вычислить определённый интеграл \(\int\limits^{ \frac{ \pi }{2} }_{ \frac{ \pi }{4} } {x*cos4x} \, dx \)


    Решение: $$ \int\limits^{ \frac{ \pi }{2} }_{ \frac{ \pi }{4} } {x*cos4x} \, dx= $$
    Так как представлен интеграл от произведения функций, то используется метод интегрирования по частям:
    $$ \int\limits {u} \, dv =uv- \int\limits {v} \, du $$
    u=x ⇒ du=dx
    dv=cos4xdx ⇒ $$ v= \int\limits^{ \frac{ \pi }{2} }_{ \frac{ \pi }{4} } {cos4x} \, dx = \frac{1}{4} sin4x|^{ \frac{ \pi }{2} }_{ \frac{ \pi }{4} }= \frac{1}{4}sin \frac{4 \pi }{2} - \frac{1}{4} sin \frac{4 \pi }{4} =0-0=0 \\ =x*0- \frac{1}{4} \int\limits^{ \frac{ \pi }{2} }_{ \frac{ \pi }{4} } {sin4x} \, dx =- \frac{1}{4}* (- \frac{1}{4} cos4x)|^{ \frac{ \pi }{2} }_{ \frac{ \pi }{4} }= \frac{cos \frac{4 \pi }{2} }{16} - \frac{cos \frac{4 \pi }{4} }{16} = \\ = \frac{1}{16} -(- \frac{1}{16} )= \frac{2}{16}= \frac{1}{8} $$

  • Вычислить определенный интеграл \( \int\limits_0^1(-2x^2+3x-x^3)dx \)


    Решение: 1            1           1                      1            1 1                         1             1          1

    S(-2x^2dx)+S3xdx+S(-x^3dx)=-2Sx^2dx+3Sxdx-Sx^3dx=-2*x^3/3!+3*x^2/2!x^4/4!= -2*1/3+3*1/2-

    0            0           0                    0              0        0                           0              0          0  

    -1/4=-2/3+3/2-1/4=-8+18-3/12=7/12

  • Вычислить определённый интеграл с точностью до второго знака после запятой \(\int\limits_2^3 x\cdot ln(x-1)dx \)


    Решение: Вводим замену переменной 
    u=x-1
    тогда х=u+1, а du=dx
    Получили интеграл
    $$ \int\limits^3_2 {(u+1)ln(u)} \, du= \int\limits^3_2 {(uln(u)+ln(u))} \, du $$
    Сначала найдём неопределённый интеграл
    $$ \int\limits {uln(u)} \, du+ \int\limits {lnu} \, du= u^2( \frac{ln(u)}{2}- \frac{1}{2^2})+(uln(u)-u)= \\ = \frac{u^2ln(u)}{2}- \frac{u^2}{4}+uln(u)-u=uln(u)( \frac{u}{2}+1)-u( \frac{u}{4}+1)+C $$
    Вводим обратную замену
    $$ (x-1)*ln(x-1)*( \frac{x-1}{2}+1)-(x-1)*( \frac{x-1}{4}+1)= \\ = \frac{1}{2} (x-1)^2*ln(x-1)+(x-1)ln(x-1)- \frac{1}{4}(x-1)^2-(x-1) = \\ = \frac{1}{4}(x-1)*(2(x-1)*ln(x-1)+4ln(x-1)-x)|^3_2= \\ =\frac{1}{4}(3-1)(2(3-1)*ln(3-1)+4ln(3-1)-3- \\ -(\frac{1}{4}(2-1)(2(2-1)*ln(2-1)+4ln(2-1)-2)= \\ = \frac{1}{2}(4ln2+4ln2-3)-( \frac{1}{4}(2ln1+4ln1-2)= \\ = \frac{1}{2}(8*0,6913-3)-( \frac{1}{4}(2*0+4*0-2))= \\ =2,7652-1,5+0,5=1,77 $$

  • Вычислить определенный интеграл \( \int\limits_0^{\frac{\pi}{2}} x cosx dx \)


    Решение: Для начала найдем неопределенный интеграл
    ∫x*cosx dx
    под интегралом находится ПРОИЗВЕДЕНИЕ двух функций ( х и cosx), значит этот интеграл нельзя вычислить по таблице интегралов.
    Для решения этого примера нужно воспользоваться МЕТОДОМ ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ:
    ∫u*dv=u*v-∫v*du, где u=x; dv=cosx; v=∫cosx=sinx; du=x’=1dx=dx
    ∫x*cosx=x*sinx-∫sinxdx=x*sinx-(-cosx)+C=x*sinx+cosx+C
    теперь можно вычислить определенный интеграл
    (см. рис)
    отв: (π/2) -1

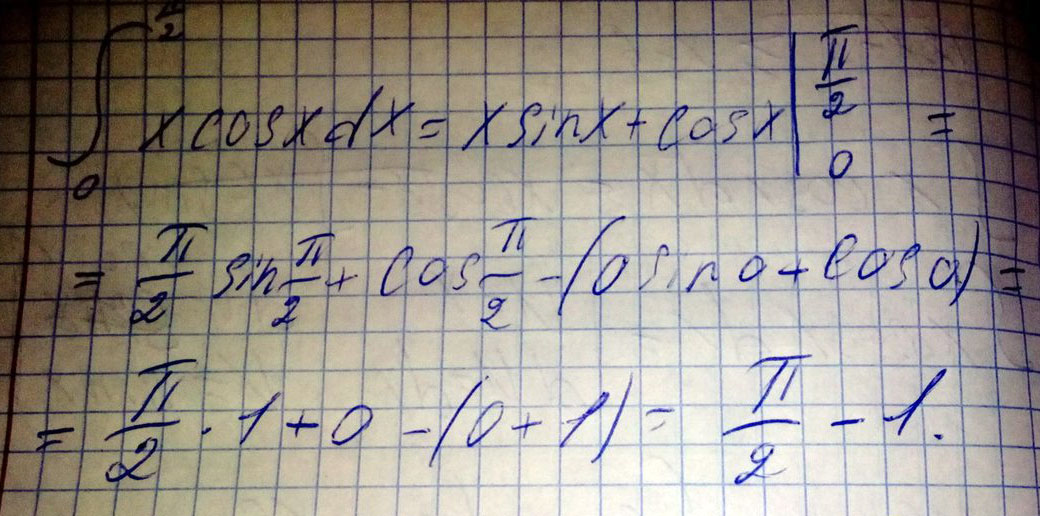
    Для начала найдем неопределенный интеграл x cosx dxпод интегралом находится ПРОИЗВЕДЕНИЕ двух функций х и cosx значит этот интеграл нельзя вычислить по таблице интегралов.Для...

  • Вычислить определенный интеграл \( \int\limits^{\frac{\pi}{2}}_0 {\frac{dx}{2+\cos{x}}} \)


    Решение: $$ \int\limits^{\frac{\pi}{2}}_0 {\frac{dx}{2+\cos{x}}} = \int\limits^{\frac{\pi}{2}}_0 {\frac{dx}{2\sin^2{(\frac{x}{2})} + 2\cos^2{(\frac{x}{2})} + \cos^2{(\frac{x}{2})} - \sin^2{(\frac{x}{2}})}} = \int\limits^{\frac{\pi}{2}}_0 {\frac{dx}{\sin^2{(\frac {x}{2})} + 3\cos^2{(\frac{x}{2})}}} =\\= \int\limits^{\frac{\pi}{2}}_0 {\frac{\frac{dx}{\cos^2{(\frac{x}{2})}}}{\tan^2{(\frac{x}{2})} + 3}} = \int\limits^{\frac{\pi}{2}}_0 {\frac{d\tan{\frac{x}{2}}}{\tan^2{(\frac{x}{2})} + 3}} = \frac{1}{\sqrt{3}}\int\limits^{\frac{\pi}{2}}_0 {\frac{d\frac{\tan{\frac{x}{2}}}{\sqrt{3}}}{(\frac{\tan{(\frac{x}{2})}}{\sqrt{3}})^2 + 1}} =\\= \frac{1}{\sqrt{3}}\arctan{\frac{\tan{\frac{x}{2}}}{\sqrt{3}}}|^{\frac{\pi}{2}}_0 = \frac{1}{\sqrt{3}}(\arctan{\frac{\tan{\frac{\pi}{4}}}{\sqrt{3}}} - \arctan{\frac{\tan{0}}{\sqrt{3}}}) = \frac{1}{\sqrt{3}}\arctan{\frac{1}{\sqrt{3}}} = \frac{\pi}{6\sqrt{3}} $$

<< < 345 6 7 > >>