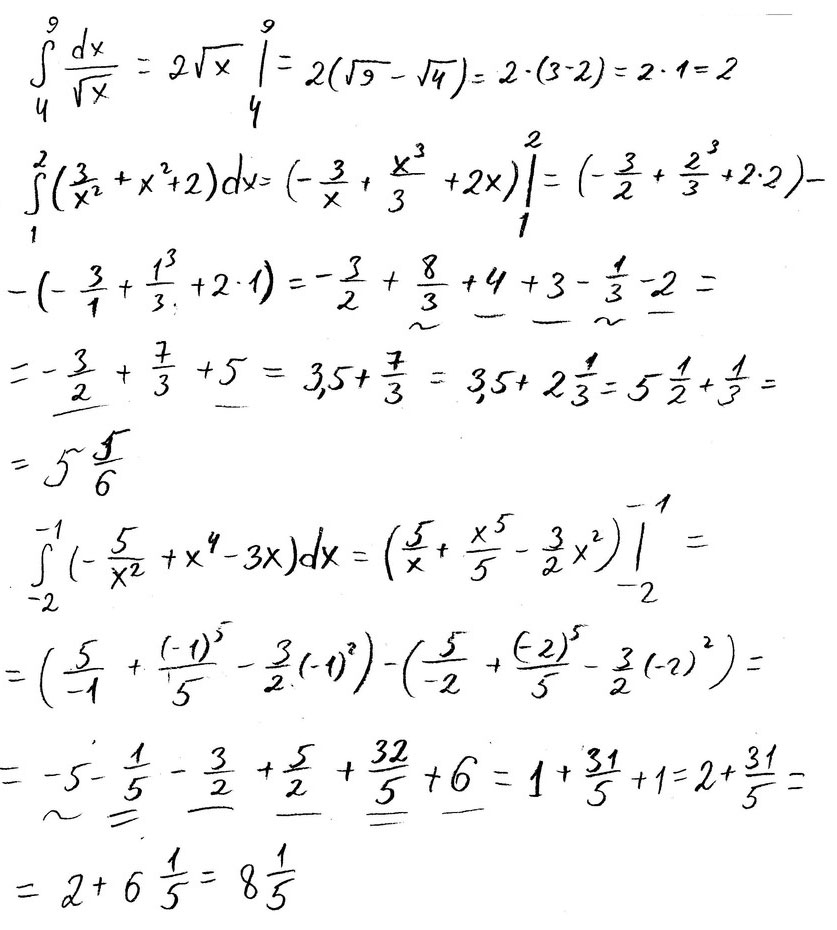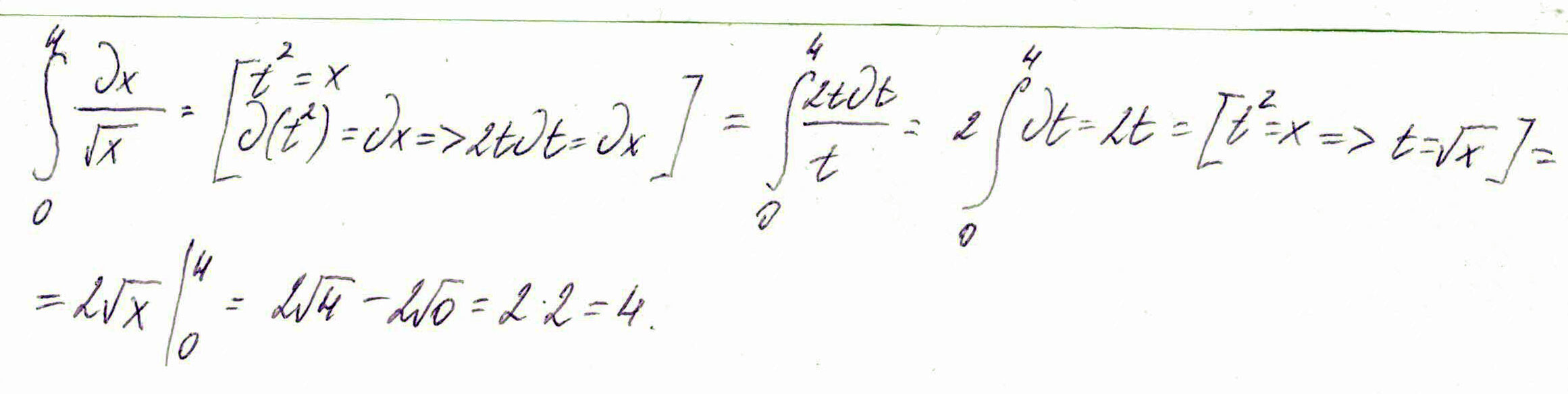интеграл »

вычислить определенный интеграл - страница 7

  • Вычислите определенный интеграл 7 задание а \( 7.a)\,\, \int\limits^4_2 {\frac{x^2+2}{x^2}} \, dx \)


    Решение: $$ 7.a)\,\, \int\limits^4_2 {\frac{x^2+2}{x^2}} \, dx =\int\limits^4_2 {(1+\frac{2}{x^2})} \, dx =(x+2*\frac{x^{-1}}{-1})|^4_2=(x-\frac{2}{x})|^4_2= \\ =4-\frac{2}4-(2-\frac{2}2)=4-\frac{1}2-1=\frac{5}2=2.5 $$

    $$ \int\limits^4_2 {(1+2/x^2)} \, dx =x-2/x|4-2=4-1/2-2+1=2,5 $$

  • Вычислите определенный интеграл \( \int\limits^9_4 { \frac{1}{\sqrt{x}}} \, dx\\ \int\limits^2_1 { (\frac{3}{x^2}+x^2+2} )dx\\ \int\limits^ {-1}_ {-2} {(\frac{-5}{x^2}+x^4-3x} ) dx \)


    Решение: $$ \int\limits^9_4 { \frac{1}{\sqrt{x}}} \, dx = |^9_4 2\sqrt{x} = 2*3-2*2=2 $$
     
      
     $$ \int\limits^2_1 { (\frac{3}{x^2}+x^2+2} )dx = |^2_1 \ \frac{-3}{x}+\frac{x^3}{3}+2x = \frac{-3}{2}+\frac{8}{3}+4 - (\frac{-3} {1}+\frac{1}{3}+2) \\ \frac{31}{6}+\frac{2}{3} = \frac{35}{6} $$
     
     
    $$ \int\limits^ {-1}_ {-2} {(\frac{-5}{x^2}+x^4-3x} ) dx = \frac{x^5}{5} - \frac{3x^2}{2} + \frac{5}{x} = \\ \frac{-1}{5}-\frac{3}{2}-\frac{5}{1} - ( \frac{-32}{5} - \frac{3*4}{2} - \frac{5}{2}) = \frac{41}{5} $$

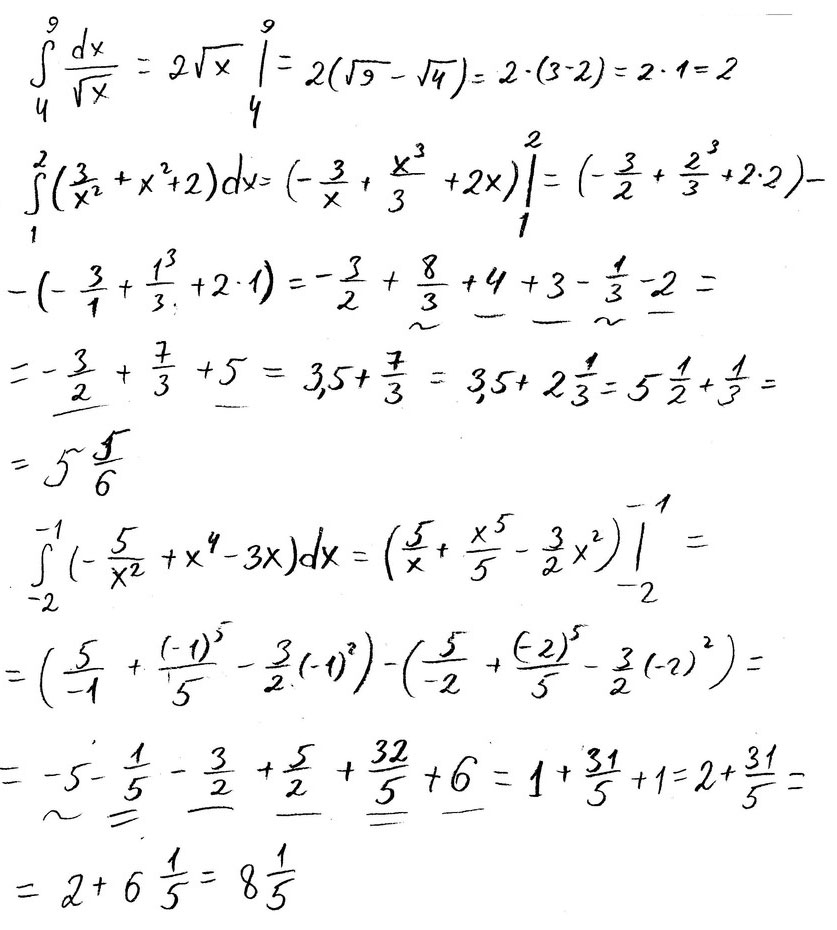
    int limits frac sqrt x dx sqrt x -       int limits frac x x dx frac - x frac x x frac - frac - frac - frac frac frac frac    int limits - - frac - x x - x dx frac x - frac x...

  • Вычислите определенный интеграл \( \int\limits_{-0,5\pi}^0 (tgx+x-3)dx \)


    Решение: \(\int\limits_{-0,5\pi}^0 (tgx+x-3)dx=\int tgx*dx+\int x*dx-3\int dx
    \int tgxdx=\int sinx \cdot \frac{dx}{cosx}\)
    Подводим cosx под знак дифференциала
    \(-\int d(cosx)/cosx=-ln/cosx/ \\ \int x*dx=(x^2)/2 \\ -3\int dx=-3x\) В сумме
    -ln/cosx/+(x^2)/2-3x
    Соответствующие значения для пределов интеграла:
    -ln/cos0/+0^2/2-3*0=-ln(1)=0
    -ln/cos(pi/2)/+(pi/2)^2/2-3*pi/2=∞
    ответ: минус ∞ (посмотри на график тангенса)

  • Вычислить определенные интегралы \( \int\limits^4_0 \frac{dx}{sqrt(x)}\)


    Решение: Решение:
    Проведем замену:
    $$ t^2=x $$
    Тогда,
    $$ d(t^2)=dx \\ 2tdt=dx $$
    Зная это, преобразуем интеграл:
    $$ 2\int\limits^4_0 \frac{tdt}{t} = 2\int\limits^4_0 dt = 2t = 2\sqrt{x} |\int\limits^4_0 = \\ = 2\sqrt4 - 2\sqrt0 = 2*2=4 $$

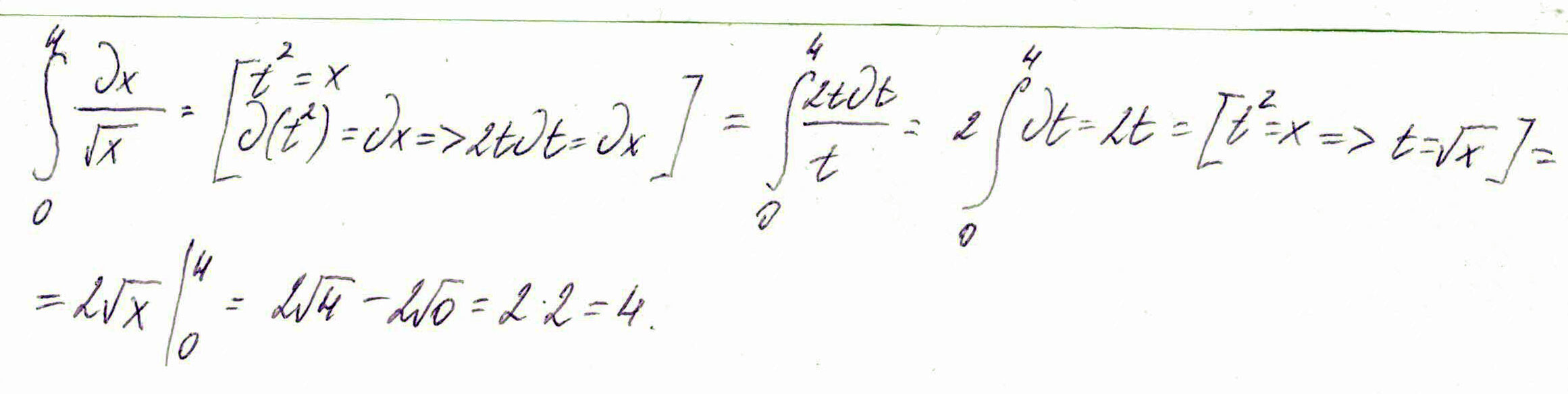
    Решение Проведем замену t x Тогда d t dx tdt dx Зная это преобразуем интеграл int limits frac tdt t int limits dt t sqrt x int limits sqrt - sqrt...

  • Вычислить определенный интеграл \( \int\limits_0^4 \frac{xdx}{\sqrt{2+4x}} \)


    Решение: Произведем замену $$ t= \sqrt{2+4x} $$
       $$ t^{2}=2+4x $$
       x=$$ \frac{1}{4}*( t^{2} -2) $$
       dx= $$ \frac{1}{2}*tdt \\ \frac{1}{8} \int\limits ({t^{2} -2}) \, dt= \frac{1}{8}( \frac{t^3}{3}-2t)= $$
    = 1/8(1/3*(2+4x)$$ \sqrt{2+4x} $$ -2$$ \sqrt{2+4x} $$)=
    1/8(6√18-2√18) - 1/8( 2/3 √2-2√2)=1/2 √18 - 1/6 √2= 4/3 * √2

<< < 567 8 9 > >>