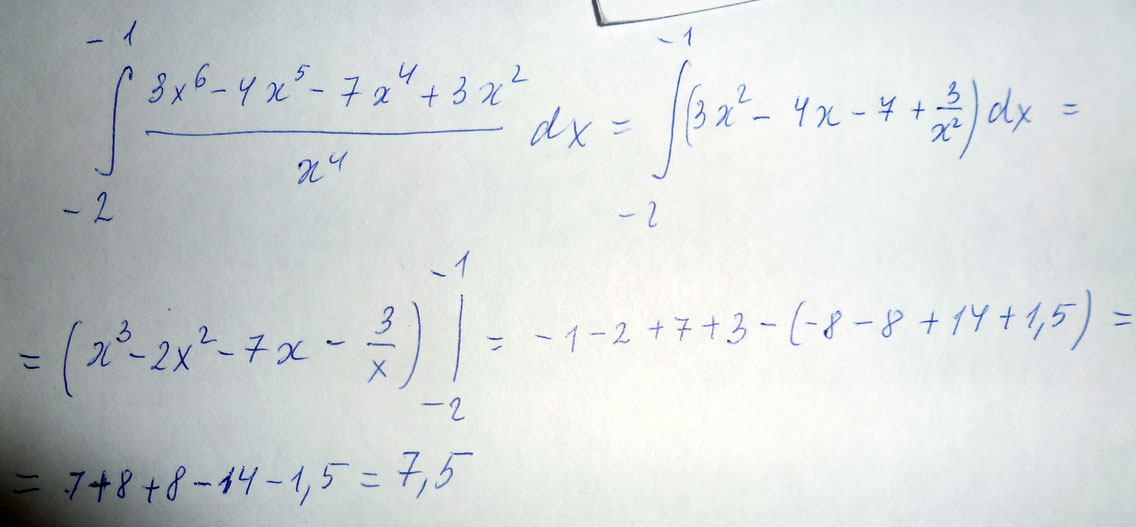интеграл »
вычислить определенный интеграл - страница 4
Вычислить неопределенные интегралы:\( a) \int\limits{x*arctg(2x)} \, dx\\ б) \int\limits { \frac{x+ln^2(x)}{x}} \, dx\\ в) \int\limits{ \frac{ \sqrt{x-2}}{1+ \sqrt{x-2} } } \, dx\\ г) \int\limits{ cos\frac{x}{ \sqrt{2} }} \, dx \)
Решение: Вычислите неопределенные интегралы
a)$$ \int\limits{x*arctg(2x)} \, dx $$
Интегрируем по частям
$$ \int\limits {U(x)} \, dV(x)=U(x)V(x)- \int\limits{V(x)} \, dU(x) \\ \int\limits{x*arctg(2x)} \, dx=\begin{vmatrix}U=arctg(2x)\, \; dU=\frac{2}{4x^2+1}dx\\dV=xdx\; V=\frac{x^2}{2} \end{vmatrix} = \ \frac{x^2}{2}*arctg(2x)- \int\limits{ \frac{x^2}{4x^2+1} } \, dx $$
Находим второй интеграл отдельно
$$ \int\limits{ \frac{x^2}{4x^2+1} } \, dx = \frac{1}{4}\int\limits{ \frac{4x^2+1-1}{4x^2+1} } \, dx=\frac{1}{4}\int\limits{(1-\frac{1}{4x^2+1} }) \, dx = \\ =\frac{1}{4}\int\limits{}dx-\frac{1}{4}\int\limits{\frac{1}{4x^2+1} } \, dx=\frac{x}{4}-\frac{1}{8}\int\limits{\frac{1}{(2x)^2+1} } \, d(2x)= \\ =\frac{x}{4}-\frac{1}{8}*arctg(2x)+C $$
Окончательно запишем
$$ \int\limits{x*arctg(2x)} \, dx =\frac{x^2}{2}*arctg(2x)+\frac{1}{8}arctg(2x)-\frac{x}{4}+C $$
б)$$ \int\limits { \frac{x+ln^2(x)}{x}} \, dx= \int\limits {(1+\frac{ln^2(x)}{x})} \, dx= \int\limits{} \, dx+\int\limits {\frac{ln^2(x)}{x}} \, dx=x+\int\limits {\frac{ln^2(x)}{x}} \, dx $$
Второй интеграл найдем отдельно
$$ \int\limits {\frac{ln^2(x)}{x}} \, dx =\begin{vmatrix}u=ln(x)\\du=\frac{1}{x}dx\end{vmatrix}= \int\limits{u^2} \, du= \frac{u^3}{3}+C= \frac{ln^3(x)}{3}+C $$
Таким образом получили
$$ \int\limits { \frac{x+ln^2(x)}{x}} \, dx=x+\ \frac{1}{3}ln^3(x)+C $$
в) $$ \int\limits{ \frac{ \sqrt{x-2}}{1+ \sqrt{x-2} } } \, dx $$
Используем замену переменных
$$ \int\limits{\frac{\sqrt{x-2}}{1+ \sqrt{x-2}}} \, dx=\begin{vmatrix}x-2=u^2 \\ dx=2udu\end{vmatrix}=\int\limits{ \frac{ 2u^2}{1+ u } }\,du= 2\int\limits{(u-1+ \frac{1}{u+1}) } \, du= \\ =u^2-2u+ ln(u+1)+C= x-2+2 \sqrt{x-2}+ln( \sqrt{x-2}+1)+C $$
г)$$ \int\limits{ cos\frac{x}{ \sqrt{2} }} \, dx= \sqrt{2} \int\limits{ cos\frac{x}{ \sqrt{2} }} \, d( \frac{x}{ \sqrt{2} } ) =\sqrt{2}*sin\frac{x}{ \sqrt{2}} +C $$
Вычислить определённый интеграл \(\int\limits_0^2 (2x^3-x-1)dx \)
Решение: Интеграл суммы равен сумме интегралов, далее находите первообразные и подставляете пределы интегрирования.
Вычислить определённый интеграл \( \int\limits_{-2}^{-1} \frac{3x^6-4x^5-7x^4+3x^2}{x^4}dx \)
Решение: = $$ \int\limits^{-1}_{-2} {(3 x^{2}-4x-7+ \frac{3}{ x^{2} } ) } \, dx $$=
$$ \int\limits^{-1}_{-2} {(3 x^{2} -4x-7)} \, dx + \int\limits^{-1}_{-2} { \frac{3}{ x^{2} } } \, dx $$=
$$ (3 x^{3}/3-4 x^{2} /2-7x) \int\limits^{-1}_{-2} + 3 \int\limits^{-1}_{-2} { x^{-2} } \, dx $$=
$$ -1-2+7-(-8-8+14)+3(- \frac{1}{x} ) \int\limits^{-1}_{-2} $$=
= -1-2+7+8+8-14-3(1/(-1) - 1/(-2)) = 6-3(-1+0.5) = 6+1.5 = 7.5
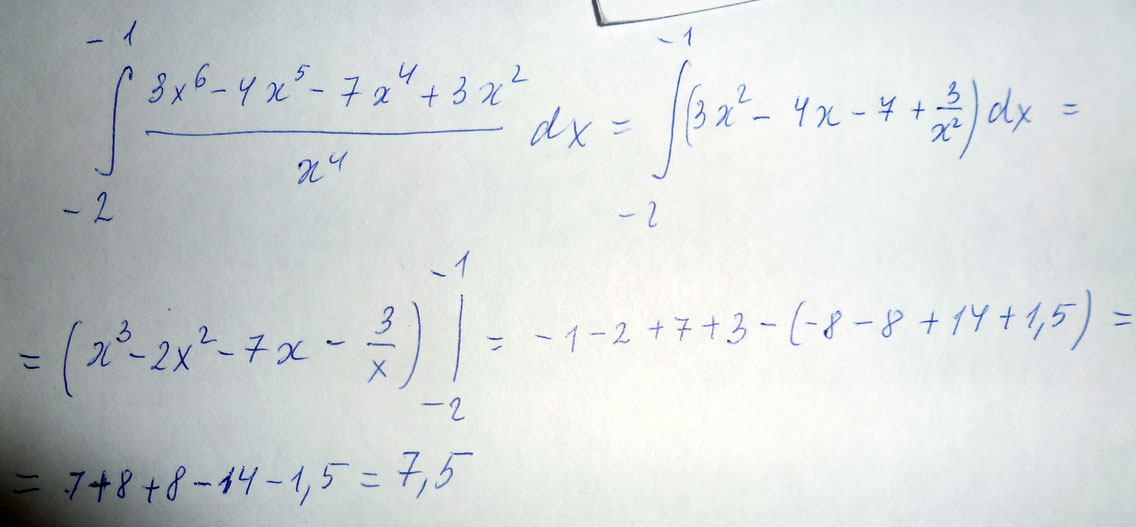
Вычислить определенный интеграл (2x^2+4x+7)cos2x
пределы наверху-пи
внизу-0
Решение: $$ \int\limits^ \pi_0 {(2x^2+4x+7)cos2x} \, dx $$
интегрируем по частям
$$ u=(2x^2+4x+7) \\ du=(4x+4)dx \\ dv=cos2x\,dx \\ v=0.5sin2x $$
Тогда
$$ \int\limits^ \pi_0 {(2x^2+4x+7)cos2x} \,dx= \\ =(2x^2+4x+7)*0.5sin2x- 0.5\int\limits^ \pi_0 {sin2x(4x+4)} \, dx $$
Получившийся интеграл опять интегрируем по частям
$$ u=(4x+4) \\ du=4dx \\ dv=sin2x\,dx \\ v=-0.5cos2x \\ \int\limits^ \pi_0 {sin2x(4x+4)} \, dx =-0.5(4x+4)cos2x+0.5\int\limits^ \pi _0 {4cos2x} \, dx = \\ =-0.5(4x+4)cos2x+2\int\limits^ \pi _0 {cos2x} \, dx = \\ =-0.5(4x+4)cos2x+sin2x $$
Окончательно получаем
$$ \int\limits^ \pi_0 {(2x^2+4x+7)cos2x} \,dx= \\ =(2x^2+4x+7)*0.5sin2x- 0.5\int\limits^ \pi_0 {sin2x(4x+4)} \, dx= \\ =(2x^2+4x+7)*0.5sin2x- 0.5(-0.5(4x+4)cos2x+sin2x)|_0^ \pi = \\ =(2x^2+4x+7)*0.5sin2x+(x+1)cos2x-0,5sin2x|_0^ \pi = \\ = \pi +1-( \pi +1)=0 $$
Вычислить определенный интеграл: \( 1)\quad \int\limits _{\frac{1}{\sqrt{e}}}^{e}\frac{dx}{x}\\ 2)\quad \int\limits^0_{-\frac{\pi}{2}} {sin(\frac{\pi}{4}-3x)} \, dx\\ 3)\quad \int \limits _0^1\, arctgx\, dx \)
Решение: $$ 1)\quad \int\limits _{\frac{1}{\sqrt{e}}}^{e}\frac{dx}{x}=ln|x|\int\limits |^{e}_{\frac{1}{\sqrt{e}}}=lne-ln\frac{1}{\sqrt{e}}=1-(ln1-ln\sqrt{e})=\\\\=1-(0-\frac{1}{2})=\frac{1}{2}\\\\2)\quad \int\limits^0_{-\frac{\pi}{2}} {sin(\frac{\pi}{4}-3x)} \, dx =-\frac{1}{3}\cdot (-cos(\frac{\pi}{4}-3x))|_{-\frac{\pi}{2}}^0=\\\\=\frac{1}{3}\left (cos\frac{\pi}{4}-cos(\frac{\pi}{4}+\frac{3\pi}{2})\right )=\frac{1}{3}\left (\frac{\sqrt2}{2}-cos\frac{7\pi}{4}\right )= \\ =\frac{1}{3}\left (\frac{\sqrt2}{2}-\frac{\sqrt2}{2}\right )=0 \\ 3)\quad \int \limits _0^1\, arctgx\, dx=[\, u=arctgx,\; du=\frac{dx}{1+x^2}\,\, dv=dx\;,\; v=x]=\\\\=x\cdot arctgx|_0^{\frac{\pi}{4}}-\int \limits _{0}^{\frac{\pi}{4}}\, \frac{x\, dx}{1+x^2} =\frac{\pi}{4}\cdot arctg\frac{\pi}{4}-\frac{1}{2}\cdot \int \limits _0^{\frac{\pi}{4}}\frac{2x\, dx}{1+x^2}=\\\\=\frac{\pi}{4}\cdot arctg\frac{\pi}{4}-\frac{1}{2}\cdot ln|1+x^2||_0^{\frac{\pi}{4}}=\\\\=\frac{\pi}{4}\cdot arctg\frac{\pi}{4}-\frac{1}{2}(ln(1+\frac{\pi ^2}{16})-ln1)= \\ =\frac{\pi}{4}\cdot arctg\frac{\pi}{4}-\frac{1}{2}ln(1+\frac{\pi ^2}{16}) $$