интеграл »
неопределенный интеграл - страница 18
Найдите неопределённый интеграл:
\( \int\limits {((2x-x)^4-17x^9+\sqrt2)} \, dx \)
Решение: $$ 2x-x=x\\\\\int ((2x-x)^4-17x^9+\sqrt2)dx=\int (x^4-17x^9+\sqrt2)dx=\\\\=\frac{x^5}{5}-17\cdot \frac{x^{10}}{10}+\sqrt2\cdot x+C $$
В скобке скорее всего была написана линейная функция, а не (2х-х). Тогда форула для интеграла будет такой:
$$ \int (kx+b)^{n}dx=\frac{1}{k}\cdot \frac{(kx+b)^{n+1}}{n+1}+C $$
Например,
$$ \int (2x-3)^4dx=\frac{1}{2}\cdot \frac{(2x-3)^5}{5}+C\\\\\int \frac{dx}{(5-3x)^4}=\int (5-3x)^{-4}dx=-\frac{1}{3}\cdot \frac{(5-3x)^{-3}}{-3}+C=\frac{1}{9(5-3x)^3}+C $$
Решить нужно неопределённый интеграл \(\int\frac{(\sqrt[3]{x^2} -1)^2}{\sqrt{x^3}} dx \)
Решение: Возвести в квадрат и почленно разделить, представив в виде дробной степени :))
$$ \int{\frac{x^{\frac49}-2x^\frac23+1}{x^{\frac13}}} \, dx = \int{ (x^{\frac19} -2x^{\frac13}+x^{-\frac13})} \, dx=\frac{x^{1\frac49}}{1\frac49}-\frac{2x^{1\frac13}}{1\frac13}+\frac{3x^\frac23}2=\\\\=\frac{9x^{1\frac49}}{13}-\frac{6x^{1\frac13}}{4}+\frac{3x^\frac23}2=\frac{9x \sqrt[9]{x} }{13}-\frac{3x \sqrt[3]{x} }{2}+\frac{3 \sqrt[3]{x^2} }{2} $$
Найдите неопределенный интеграл \(\int arctg\sqrt{6x-1} dx \)
Решение: Для начала делаем замену:
$$ t= \sqrt{6x-1} \\ dt= \frac{3dx}{ \sqrt{6x-1} } = \frac{3dx}{t} \\ dx= \frac{tdt}{3} $$
Получаем такой интеграл: $$ \int\limits arctgt \frac{tdt}{3} $$
Берем его по частям:
$$ u=arctgt \\ du= \frac{dt}{t^2+1} \\ dv= \frac{tdt}{3} \\ v = \frac{t^2}{6} \\ \int\limits udv=uv-\int\limits vdu \\ \int\limits arctgt \frac{tdt}{3} = \frac{t^2arctgt}{6} - \frac{1}{6} \int\limits \frac{t^2}{t^2+1}dt = \frac{1}{6} (t^2arctgt-\int\limits \frac{t^2+1-1}{t^2+1}dt )= \\ = \frac{1}{6} (t^2arctgt-\int\limits (1-\frac{1}{t^2+1})dt )=\frac{1}{6} (t^2arctgt+arctgt -t)+C= \\ =\frac{t^2+1}{6} arctgt - \frac{t}{6} +C $$
Теперь обратная замена и ответ:
$$ t= \sqrt{6x-1} \\ t^2=6x-1 \\ \int\limits arctg \sqrt{6x-1} dx=xarctg \sqrt{6x-1} - \frac{\sqrt{6x-1}}{6} +C $$
Решить неопределенный интеграл \( 1) \int\limits { \frac{4}{x} } \, dx \\ \int\limits { \frac{1}{ \sqrt[3]{x} } } \, dx \)
Решение: $$ 1) \int\limits { \frac{4}{x} } \, dx =4\int\limits { \frac{1}{x} } \, dx=4\ln|x|+C $$
2)
$$ \int\limits { \frac{1}{ \sqrt[3]{x} } } \, dx=\int\limits { x^{- \frac{1}{3}} } \, dx= \frac{x^{- \frac{1}{3}+1} }{- \frac{1}{3}+1} +C= \dfrac{3 \sqrt[3]{x^2} }{2} +C $$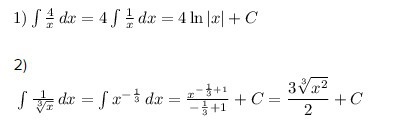
Найдите неопределенный интеграл \( \int\limits {\frac{dx}{sinx\sqrt{1+cosx}}} \, dx \)
Решение: $$ \int\limits {\frac{dx}{sinx\sqrt{1+cosx}}} \, dx =[\, cos^2\frac{x}{2}=\frac{1+cosx}{2},\sqrt{1+cosx}=\sqrt{2cos^2\frac{x}{2}}=\sqrt2cos\frac{x}{2}\, ]=\\=\int \frac{dx}{sinx\cdot \sqrt2\cdot cos\frac{x}{2}} =\int \frac{dx}{2sin\frac{x}{2}\cdot cos\frac{x}{2}\cdot \sqrt2cos\frac{x}{2}}=\frac{1}{2\sqrt2}\int \frac{(sin^2\frac{x}{2}+cos^2\frac{x}{2})dx}{sin\frac{x}{2}\cdot cos^2\frac{x}{2}} =\\\\=\frac{1}{2\sqrt2}\int (\frac{sin\frac{x}{2}}{cos^2\frac{x}{2}}+\frac{1}{sin\frac{x}{2}})dx=\frac{1}{2\sqrt2}\int \frac{sin\frac{x}{2}dx}{cos^2\frac{x}{2}}+\frac{1}{2\sqrt2}\int \frac{sin\frac{x}{2}dx}{sin^2\frac{x}{2}} = \\ =\frac{1}{2\sqrt2}\int \frac{-2dt}{t^2}\; \; [\, t=cos\frac{x}{2},dt=-\frac{1}{2}sin\frac{x}{2}dx\, ]+\frac{1}{2\sqrt2}\int \frac{sin\frac{x}{2}dx}{1-cos^2\frac{x}{2}}=\\\\=-\frac{1}{\sqrt2}\cdot \frac{t^{-1}}{-1} +\frac{1}{2\sqrt2}\int \frac{-2dt}{1-t^2} =\frac{1}{\sqrt2\, t}-\frac{1}{\sqrt2}\int \frac{dt}{-(t^2-1)}=\\\\=\frac{1}{\sqrt2\, t}+\frac{1}{\sqrt2}\cdot \frac{1}{2}\cdot ln\left |\frac{t-1}{t+1} \right |+C= \\ =\frac{1}{\sqrt2cos\frac{x}{2}}+\frac{1}{2\sqrt2}\cdot ln\left |\frac{cos\frac{x}{2}-1}{cos\frac{x}{2}+1}\right |+C $$