интеграл »
неопределенный интеграл - страница 16
Решить неопределенный интеграл
(sin2x)^4dx
Решение: $$ \int\ {(sin2x)^4} \, dx \\ 2x=m \\ dx= \frac{1}{2}dm \\ = \frac{1}{2} \int\sin^{4}m \, dm= \frac{1}{2} \int\ \frac{(1-cos2m)^2}{2^2} \, dm \\ = \frac{1}{8} \int\((1-2cos2m+cos^{2}2m) \, dm= \\ = \frac{1}{8}m- \frac{1}{4}* \frac{1}{2}sin2m+ \frac{1}{8} \int\ {cos^{2}2m} \, dm \\ = \frac{1}{8}m- \frac{1}{8}sin2m+ \frac{1}{8} \int\ { \frac{1+cos4m}{2} } \, dm \\ = \frac{1}{8}m- \frac{1}{8}sin2m+ \frac{1}{16}m+ \frac{1}{16}* \frac{1}{4}sin4m \\\\ = \frac{1}{8}2x- \frac{1}{8}sin4x+ \frac{1}{16}2x+ \frac{1}{16} \frac{1}{4}sin8x \\ = \frac{x}{4}- \frac{sin4x}{8}+ \frac{x}{8}+ \frac{sin8x}{64} \\ = \frac{3x}{8} - \frac{sin4x}{8}+ \frac{sin8x}{64}+C $$
Вычислите неопределенный интеграл s (3-sin 2x) dx
Решение: Прилагаю таблицу интегралов.
Интеграл суммы(разности) равен сумме(разности) интегралов, т. е.:
s (3-sin2x)dx=s (3)dx - s (sin2x)dx=3x + C1 - 1/2*s (sin2x)d2x=
1/2 перед интегралов выносим, чтобы под дифференциалом х умножить на 2, т. е. как бы умножаем и делим на одно и то же число, чтобы ничего не изменилось. Делаем это для того, чтобы переменная интегрирования стала такой же, как и аргумент синуса, чтобы его можно было проинтегрировать.
=3х+C1-1/2*(-cos(2x))+C2=3x+C1+1/2*cos2x+C2
С1 и С2 - это константы, которые появляются в неопределенном интеграле, их можно объединить в одну, т. е. С1+С2=С. Тогда получим итоговое выражение:
3х+1/2*cos2x+C
Найдите неопределённый интеграл : \( \int\limits sin2xdx \)
Решение: $$ \int\limits {sin2x} \, dx = $$
Сделаем замену: u=2x du=2dx
$$ = \frac{1}{2} \int\limits {sin(u)} \, du =- \frac{cos(u)}{2} +C=- \frac{1}{2} cos(2x)+C $$
Ответ смотри в приложении:
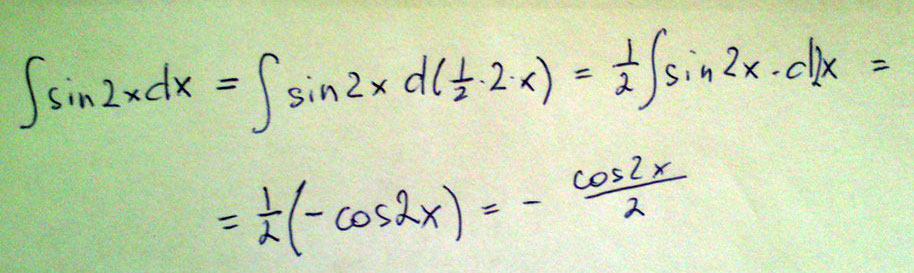
Вычислить неопределенный интеграл (
\( \int\limits {(1-x+2x^2)sin4x} \, dx \)
Решение: Int (1 - x + 2x^2)*sin 4x dx = Int sin 4x dx - Int x*sin 4x dx + 2*Int x^2*sin 4x dx =
= -1/4*cos 4x - |u=x, dv=sin 4x dx, du=dx, v=-1/4*cos 4x| +
+ |u=x^2, dv=sin 4x dx, du=2x dx, v=-1/4*cos 4x| =
= -1/4*cos 4x + x/4*cos 4x - 1/4*Int cos 4x dx - x^2/2*cos 4x + Int x*cos 4x dx =
= -1/4*cos 4x + x/4*cos 4x - 1/16*sin 4x - x^2/2*cos 4x +
+ |u=x, dv=cos 4x dx, du=dx, v=1/4*sin 4x| =
= -1/4*cos 4x + x/4*cos 4x - 1/16*sin 4x - x^2/2*cos 4x +
+ x/4*sin 4x - 1/4*Int sin 4x dx =
= -1/4*cos 4x + x/4*cos 4x - 1/16*sin 4x - x^2/2*cos 4x +
+ x/4*sin 4x + 1/16*cos 4x + C
Решить неопределенный интеграл(интегрирование по частям):
\( x*ln*(x^2+1)*dx \)
Решение: $$ \int x \ln(x^2+1)dx = \frac{1}{2}\int(\ln(x^2+1))d(x^2+1) = \frac{1}{2}\int(\ln t)dt $$Интегрирование логарифма производится по частям
представим, что
$$ u = \ln t; v = t\\ du = u’dt = \frac{dt}{t}\\ dv = v’dt = dt\\ \int \ln t dt = \int u dv = uv - \int vdu = t \ln t - \int t\frac{dt}{t} = \\ = t \ln t - \int dt = t \ln t - t +C $$
далее вернемся к нашему интегралу:
$$ \frac{1}{2}\int \ln t dt =\frac{t \ln t - t}{2} + C = \frac{x^2+1}{2}\ln (x^2+1) - \frac{x^2+1}{2} + C = \\ =\frac{x^2+1}{2}\ln(\frac{x^2+1}{e}) + C $$