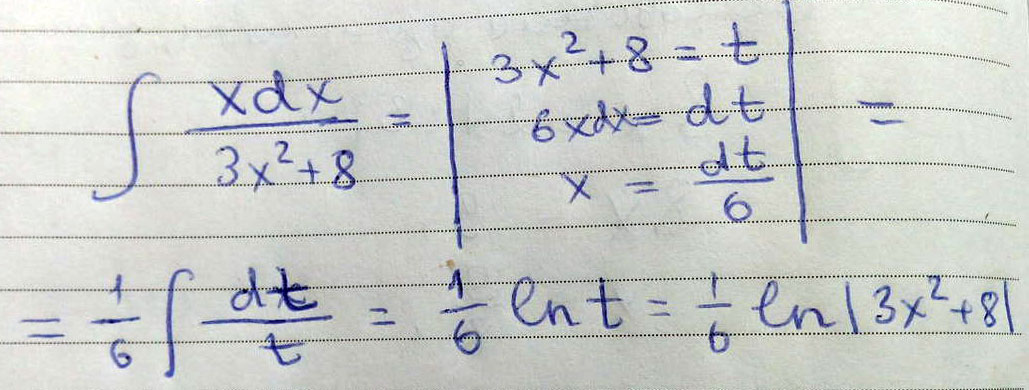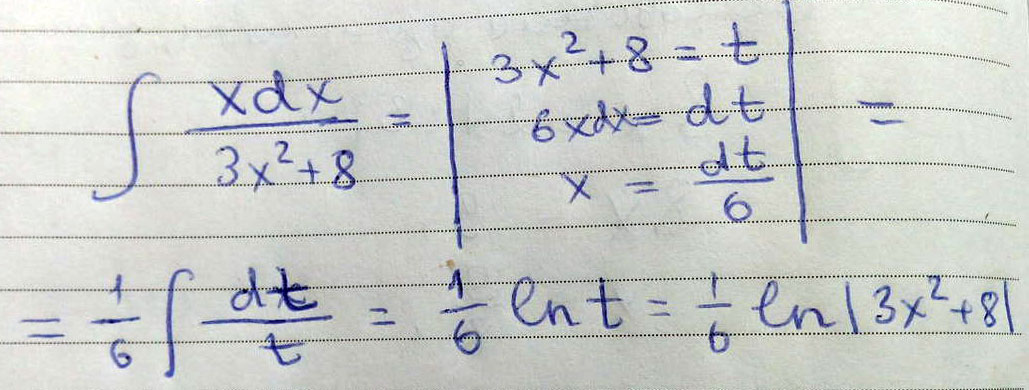интеграл »
неопределенный интеграл - страница 2
Интеграл ( 1+ x5) в степени 7 dx
Интеграл sin в квадрате х умножить на cosX dx
на и неопределенный интеграл
Решение: Всё это решается через первообразной.
В первом функция составная
$$ \int\limits {(1+x^5)^7} \, dx= \int\limits {(x^{35}+7x^{30}+21x^{25}+35x^{20}+35x^{15}+21x^{10}+7x^5+1)} \, dx= \\ = \frac{x^{36}}{36} + \frac{7x^{31}}{31}+ \frac{21x^{26}}{26}+ \frac{5x^{21}}{3} + \frac{35x^{16}}{16} + \frac{21x^{11}}{11}+ \frac{7x^6}{6}+x+C \\ \int\limits {\sin^2x\cdot \cos x} \, dx = \int\limits {(1-\cos^2x)\cos x} \, dx = \frac{\sin^3x}{3} +C $$
Вычислить неопределённый интеграл методом неопределенных коэффициентов, подробно.
13/(х^2+4)(x+3)dx
Решение: 13/((x^2 + 4)(x+3))
Убеждаемся, что знаменатель разложить на более "мелкие" множители мы уже не можем:
x^2 + 4 =0 - корней нет, значит, разложить на множители не получится
(A*x + B)/(x^2 + 4) + C/(x+3) = 13/((x^2 + 4)(x+3)) - представляем нашу дробь в виде суммы таких дробей. Приводим к более наглядному виду:
(А*x^2 + 3A*x + B*x + 3B + C*x^2 + 4C) = 13. Знаменатели опустил, т. к. они одинаковые и очевидные.
Составляем простенькую систему уравнений, приравнивая коэффициенты перед соответствующими степенями:
A + C = 0
3A + B = 0
3B + 4C = 13
A = - C
B = -3A = 3C
9C + 4C = 13
C = 1
A =-1
B =3
Т. о. исходный интеграл свели к сумме двух интегралов:
S (3-x)/(x^2 + 4) dx + S 1/(x + 3)dx
При этом первый можно разбить еще на два:
S 3/(x^2 + 4) dx - S x/(x^2 + 4) dx + S 1/(x + 3) dx
S 3/(x^2 + 4) dx = (3/2)*arctg(x/2) + C - табличный интеграл
S 1/(x + 3) dx = ln(x + 3) + c - табличный
S x/(x^2 + 4) dx = 1/2 *S 1/(x^2 + 4) d(x^2 + 4) = 0.5 * ln(x^2 + 4) + c - аналогично предыдущему.
Ответ: (3/2)*arctg(x/2) + ln(x + 3) + (1/2)* ln(x^2 + 4) + cНайти неопределенные интегралы и правильность полученных результатов проверить дифференцированием 1) интеграл (x+12)dx/x^2-x-6 2) интеграл arctg 4x dx Решить подробно)
Решение: x dx 1 2x dx 1 d(7+x²) 1 ∫ -= - ∫- =- ∫ - =- ln(7+x²)+C 7+x² 2 7+x² 2 7+x² 2 [1/2 *ln(7+x²)+C ]¹= 1/2*[ 2x /(7+x²)+0]= x /(7+x²) x+18 (x-2)+20 1 2(x-2) dx 2) ∫-dx=∫ - dx= - ∫- dx+20 ∫ - = x²-4x-12 (x-2)²-16 2 (x-2)²-16 (x-2)²-16 1 1 | x-2-4 | 1 5 | x-6 | =- *ln|(x-2)²-16|+20 *- *ln |-| +C= - *ln |x²-4x-12|+-*ln |-| +C 2 2*8 | x-2+4 | 2 4 | x+2 | 3) ∫(3-x) cosx dx=[ u=3-x, du=-dx, dv=cosx dx, v=sinx ] =(3-x)sinx+∫ sinx dx= =(3-x)sinx-cosx+C [(3-x)sinx-cosx]¹= -sinx+(3-x)cosx+sinx +0=(3-x)cosx
найдите неопределенные интегралы. правильность полученных результатов проверьте дефференцированием. а) интеграл(x^4-1/2х-4)dx
б) интергал х^2 под корнем 3х-7dx
Решение: $$ \frac{1}{2} \int\limits { \frac{ x^{4} -1}{x-2} } \, dx $$
если поделить многочлен на многочлен, то получим
$$ \frac{ x^{4} -1}{x-2} = x^{3} +2 x^{2} +4x +8 + \frac{15}{x-2} $$
если проинтегрировать каждое слагаемое,
то получим: $$ \frac{1}{2} ( \frac{ x^{4} }{4}+ \frac{2 x^{3} }{3} + \frac{4 x^{2} }{2} +8x+15ln|x-2|) +C $$
Проверить можно, взяв производную полученного выражения
б) $$ \int\limits { x^{2} \sqrt{3x7} } \, dx = \left[\begin{array}{ccc}3x-7 =t&3dx= dt\\x= \frac{t+7}{3}& dx= \frac{1}{3} dt\end{array}\right] $$=
$$ \frac{1}{3} * \frac{1}{9} \int\ {(t+7) ^{2}t } \, dt = \frac{1}{27} \int\ {(t ^{3} +14 t^{2}+7t) } \, dt $$=
=$$ \frac{1}{27} ( \frac{ t^{4} }{4} + \frac{14 t^{3} }{3} + \frac{7 t^{2} }{2}) +C= $$
=$$ \frac{(3x-7) ^{2} }{108} + \frac{14(3x-7) ^{ \frac{3}{2} } }{81} + \frac{7(3x-7)}{54} +C $$Найти неопределённый интеграл: xdx/3x^2+8
Решение: $$ \int\limits { \frac{x}{3 x^{2} +8} } \, dx =* \\ \\ u=3 x^{2} +8; \\ \frac{du}{6} =x dx==\ > \ \\ \\ \frac{1}{6} \int\limits { \frac{du}{u} } \, = \frac{1}{6} lnu==\ > \ \\ \\ *=\frac{1}{6} ln(3 x^{2} +8)+C $$