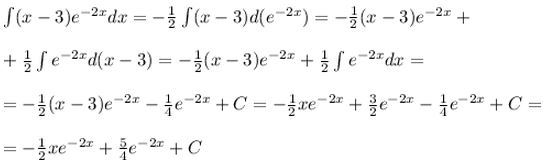интеграл »
неопределенный интеграл - страница 3
Решить неопределенный интеграл∫ dx/(3x^2+2x-1)
Решение: $$ \int\frac{dx}{3x^2+2x-1}=\int\frac{dx}{3(x+1)(x-\frac{1}{3})}=\int\frac{dx}{(x+1)(3x-1)}=\\\\=[\frac{1}{(x+1)(3x-1)}=\frac{A}{x+1}+\frac{B}{3x-1}=\frac{A(3x-1)+B(x+1)}{(x+1)(3x-1)}\Rightarrow \\\Rightarrow1=A(3x-1)+B(x+1)\\x=-1:\ \ \ \ 1=A(3*(-1)-1)+B*0\rightarrow A=-\frac{1}{4}\\x=\frac{1}{3}:\ \ \ \ \ \ 1=A*0+B(\frac{1}{3}+1)\rightarrow B=\frac{3}{4}\\\frac{1}{(x+1)(3x-1)}=\frac{-\frac{1}{4}}{x+1}+\frac{\frac{3}{4}}{3x-1}=\frac{3}{4(3x-1)}-\frac{1}{4(x+1)}]= \\ \\\\\int(\frac{3}{4*3(x-\frac{1}{3})}-\frac{1}{4(x+1)})dx=\frac{1}{4}\int\frac{1}{x-\frac{1}{3}}-\frac{1}{4}\int\frac{1}{x+1}=\\=\frac{1}{4}ln|x-\frac{1}{3}|-\frac{1}{4}ln|x+1|+C $$
Решить неопределенный интеграл.
(x^3+x)/(x^4+1) dx
Решение: $$ \int\limits {\frac{x^3 + x}{x^4+1}} \, dx = \int\limits {\frac{x^3}{x^4+1}} \, dx + \int\limits {\frac{x}{x^4+1}} \, dx $$ $$ = \frac{1}{4} \int\limits {\frac{dx^4}{x^4+1}} + \frac{1}{2} \int\limits {\frac{dx^2}{x^4+1}} = \frac{1}{4} ln(x^4+1) + \frac{1}{2} arctg (x^2) + C $$
Здесь использовались замены $$ d(x^4) = 4 x^3 dx, d(x^2) = 2x dx $$
И табличные интегралы $$ \int\limits {\frac{1}{y+1}} \, dx = ln|y + 1| + C \\ \int\limits {\frac{1}{y^2+1}} \, dx = arctg(y) + C $$
найти неопределенный интеграл по частям
интеграл 3xlnxdx
Решение: Решение:
Основная формула:
$$ \int udv = uv-\int vdu $$
Тройку как константу мы можем вынести за знак интеграла:
$$ \int 3xlnxdx = 3\int xlnxdx $$
Вводим обозначения:
$$ u = ln x => du = \frac{dx}{x} \\ dv = xdx => v = \frac{x^2}{2} $$
Теперь подставляем в формулу:
$$ \int 3xlnxdx = 3(\frac{x^2lnx}{2}-\int \frac{x^2dx}{2x}) = \\ 3(\frac{x^2lnx}{2}-\frac{1}{2}\int \frac{x^2dx}{x}) = 3(\frac{x^2lnx}{2}-\frac{1}{2}\int xdx) = \\ = 3(\frac{x^2lnx}{2}-\frac{x^2}{4}+C) $$
Здравствуйте, найти неопределенный интеграл пользуясь методом разложения по частям. интеграл (x-3)e^(-2x)dx
Решение: $$ \int (x-3)e^{-2x}dx=- \frac{1}{2} \int (x-3)d(e^{-2x})=- \frac{1}{2}(x-3)e^{-2x}+\\ \\ +\frac{1}{2} \int e^{-2x} d(x-3) = - \frac{1}{2}(x-3)e^{-2x}+\frac{1}{2} \int e^{-2x} dx=\\ \\ = - \frac{1}{2}(x-3)e^{-2x}-\frac{1}{4}e^{-2x} +C= -\frac{1}{2}xe^{-2x}+\frac{3}{2}e^{-2x}-\frac{1}{4}e^{-2x} +C = \\ \\ = -\frac{1}{2}xe^{-2x}+\frac{5}{4}e^{-2x} +C $$$$ \int\ {(x-3)e^{-2x}} \, dx = \int\ {xe^{-2x}} \, dx-3 \int\ {e^{-2x}} \, dx = \\ =(- \frac{x}{2}e^{-2x}+ \frac{1}{2} \int\ {e^{-2x}} \, dx ) -3 \int\ {e^{-2x}} \, dx = \\ =- \frac{x}{2}e^{-2x}- \frac{5}{2} \int\ {e^{-2x}} \, dx = =- \frac{x}{2}e^{-2x}- \frac{5}{2}*(- \frac{1}{2}e^{-2x})= \\ = \frac{5}{4}e^{-2x}- \frac{x}{2}e^{-2x}+C $$
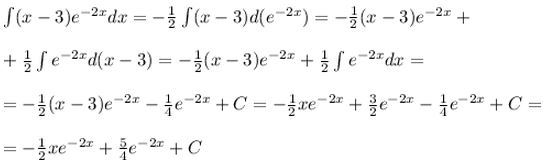
Задание 6.
Исследовать функцию и построить ее график.
y= x - 3x^2
Задание 7.
Найти неопределенный интеграл.
∫cosx*sin^3 xdx
Решение: $$ 7.\; \; \int cosx\cdot sin^3x\, dx=[\, t=sinx,\; dt=cosx\, dx\, ]=\int t^3\, dt=\\\\=\frac{t^4}{4}+C=\frac{sin^4x}{4}+C\\\\6.\; \; y=x-3x^2\\\\y’=1-6x=0,\; x=\frac{1}{6},\; \\\\+++(\frac{1}{6})-\\\\x_{max}=\frac{1}{6},\; y_{max}=\frac{1}{6}-3\cdot (\frac{1}{6})^2=\frac{1}{6}-\frac{3}{36}=\frac{1}{12}\\\\y’’=-6e 0 \; -\; net\; tochek\; peregiba $$
Асимптот нет.
График - парабола.
Пересечение с осью ОХ : $$ x-3x^2=0 $$.
$$ x(1-3x)=0\\\\x_1=0,\; x_2=\frac{1}{3}\\\\(0,0),\; (\frac{1}{3},0) $$