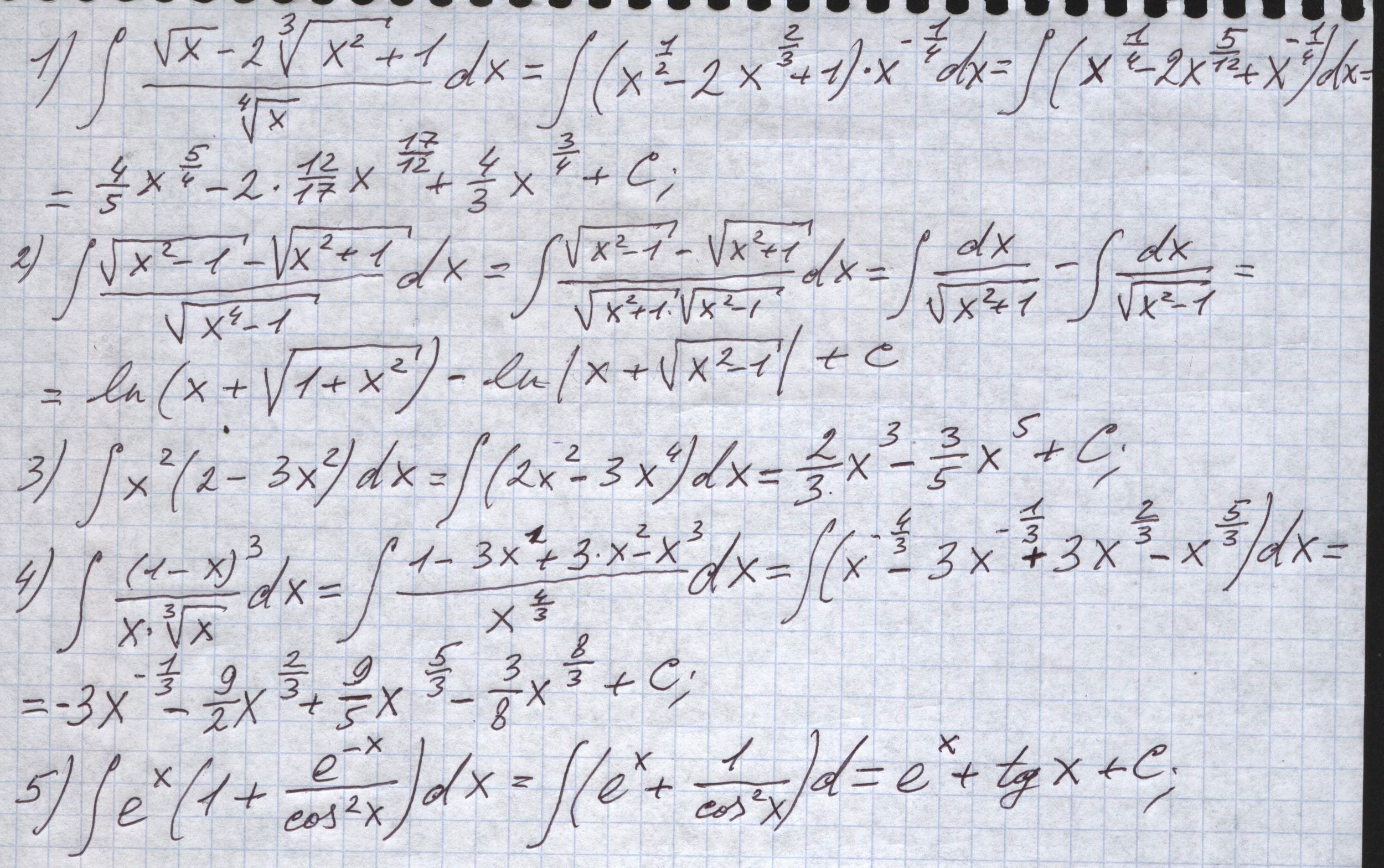интеграл »

вычислить интеграл - страница 18

  • Вычислить интегралы \( 2.\;\int_{-1}^2(x^2-1)^3dx\\ 3.\;\int_0^1e^{x^2}xdx\\ 4.\;\int_0^{\frac\pi2}\sqrt{3\sin x+1}\cos xdx\\ 5.\;\int_0^{\frac\pi2}\frac{\cos xdx}{2+\sin x}\\ 6.\;\int_1^4\frac{xdx}{25+x^2}\\ 7.\;\int_0^2\frac{4xdx}{(x^2-1)^3} \)


    Решение: $$ 2.\;\int_{-1}^2(x^2-1)^3dx=\int_{-1}^2(x^6-3x^4+3x^2-1)dx=\\=\left.\left(\frac17x^7-\frac35x^5+x^3-x\right)\right|_{-1}^2=\frac17\cdot2^7-\frac35\cdot2^5+2^3-2=\\=\frac{128}7-\frac{96}5+8-2+\frac17-\frac35+1-1=\frac{129}7-\frac{99}5+6=\\=\frac{645-693+210}{35}=\frac{162}{35}=4\frac{22}{35}\\3.\;\int_0^1e^{x^2}xdx=\left.\left(\frac12e^{x^2}\right)\right|_0^1=\frac12e^1-\frac12e^0=\frac12e-\frac12=\frac12(e-1) \\ 4.\;\int_0^{\frac\pi2}\sqrt{3\sin x+1}\cos xdx=\int_0^{\frac\pi2}\frac12\cdot(3\sin x+1)^\frac12d(3\sin x+1)=\\=\left.\left(\frac29(3\sin x+1)^{\frac32}\right)\right|_0^{\frac\pi2}=\\=\frac29\cdot\left.\left(3\sin x+1\right)^{\frac32}\right|_0^{\frac\pi2}=\frac29\cdot\left((3\cdot1+1)^\frac32-(3\cdot0+1)^{\frac32}\right)=\\=\frac29\cdot(\sqrt[3]{16}-1) \\ 5.\;\int_0^{\frac\pi2}\frac{\cos xdx}{2+\sin x}=\int_0^{\frac\pi2}\frac{d(2+\sin x)}{2+\sin x}=\left.\ln(2+\sin x)\right|_0^{\frac\pi2}=\\=\ln(2+\sin\frac\pi2)-\ln(2+\sin0)=\ln3-\ln2=\ln\frac32 \\ 6.\;\int_1^4\frac{xdx}{25+x^2}=\int_1^4\frac12\cdot\frac{d(25+x^2)}{25+x^2}=\frac12\cdot\int_1^4\cdot\frac{d(25+x^2)}{25+x^2}=\left.\frac12\cdot\ln(25+x^2)\right|_1^4=\\=\frac12(\ln(25+16)-\ln(25+1))=\frac12\ln\frac{41}{26}\\7.\;\int_0^2\frac{4xdx}{(x^2-1)^3}=\int_0^22\cdot\frac{d(x^2-1)}{(x^2-1)^3}=2\cdot\int_0^2\frac{d(x^2-1)}{(x^2-1)^3}=2\cdot\left.\left(-\frac12\cdot\frac1{(x^2-1)^2}\right)\right|_0^2=\\=\left.\left(-\frac1{(x^2-1)^2}\right)\right|_0^2=-\frac1{(4-1)^2}+\frac1{(0-1)^2}=1-\frac19=\frac89 $$

  • вычислить интегралы:

    1) int (5-4x) от -2 до 1, ответ 21

    2) int (6x^2-2x+5) от 0 до 2

    3) int sinx*dx от пи/3 до 2пи/3

    4) int (4x^3 + 6x)dx от -2 до 1


    Решение: 1                                        1

     ∫ (5 - 4*x) dx = (5*x - 2*x²) I     = (5 * 1 - 2 * 1²) - (5*(-2) - 2 * (-2)²) = 3 - (-18) = 21

    -2                                        -2

     2                                                     2

     ∫ (6*x² - 2*x + 5) = (2*x³ - x² + 5*x) I = (2 * 2³ - 2² + 5 * 2) - 0 = 16 - 4 + 10 = 22

     0                                                    0

    2*π/3                         2*π/3

      ∫    cos x dx = sin x I             = sin 2*π/3 - sin π/3 = √ 3 / 2 - √ 3 / 2 = 0

    π/3                            π/3 

     1                                             1

     ∫ (4*x³ + 6*x) dx = (x⁴ + 3*x²) I     = (1⁴ + 3*1²) - ((-2)⁴ + 3*(-2)²) = (1 + 3) - (16 + 12) =

    -2                                            -2

    = 4 - 28 = -24

  • Вычислить интеграл: \(\int\limits_1^3 x(x-10)^{10}dx \)


    Решение: int от 1 до 3 x*(x-10)^10 dx

    Интегрируем по частям

    int udv=uv- int vdu

    u=x

    du=dx

    dv=(x-10)^10dx

    v=(x-10)^11/11

    тогда

    int от 1 до 3 x*(x-10)^10 dx = x*(x-10)^11/11 от 1 до 3 - int от 1 до 3 (x-10)^11/11 dx =x*(x-10)^11/11 от 1 до 3 -(1/11)*(1/12)(x-10)^12 от 1 до 3 =

    =(3*(3-10)^11/11-(3-10)^12/132-3(1-10)^11/11+(1-10)^12/132 =

    =3*(-7)^11/11-(-7)^12/132-3*(-9)^11/11+(-9)^12/132

  • Вычислить интегралы \( 1)\; \; \int \frac{\sqrt{x}-2\sqrt[3]{x^2}+1}{\sqrt[4]{x}} dx \\ 2)\; \; \int \frac{\sqrt{x^2-1}-\sqrt{x^2+1}}{\sqrt{x^4-1}} dx \\ 3)\; \; \int x^2(2-3x^2)dx \\4)\; \; \int \frac{(1-x)^3}{x\sqrt[3]{x}}dx\\ 5)\; \; \int e^{x}(1+\frac{e^{-x}}{cos^2x})dx \)


    Решение: $$ 1)\; \; \int \frac{\sqrt{x}-2\sqrt[3]{x^2}+1}{\sqrt[4]{x}} dx=\int (x^{\frac{1}{4}}-2x^{\frac{5}{12}}+x^{-\frac{1}{4}} )dx=\\\\=\frac{4x^{\frac{5}{4}}}{5}-2\cdot \frac{12x^{\frac{17}{12}}}{17}+\frac{4x^{\frac{3}{4}}}{3}+C\\\\2)\; \; \int \frac{\sqrt{x^2-1}-\sqrt{x^2+1}}{\sqrt{x^4-1}} dx=\int \frac{\sqrt{x^2-1}-\sqrt{x^2+1}}{\sqrt{(x^2-1)(x^2+1)}}dx=\int \frac{1}{\sqrt{x^2+1}}dx-\int \frac{1}{\sqrt{x^2-1}}dx\\\\=ln|x+\sqrt{x^2-1}|-ln|x+\sqrt{x^2-1}|+C \\ 3)\; \; \int x^2(2-3x^2)dx=\int (2x^2-6x^4)dx=\\\\=2\cdot \frac{x^3}{3}-6\cdot \frac{x^5}{5}+C\\\\4)\; \; \int \frac{(1-x)^3}{x\sqrt[3]{x}}dx=\int \frac{1-3x+3x^2-x^3}{x^{\frac{4}{3}}}dx=\\\\=\int (x^{-\frac{4}{3}}-3x^{-\frac{1}{3}}+3x^{\frac{2}{3}}-x^{\frac{5}{3}})dx=-4x^{-\frac{1}{4}}-9\frac{x^\frac{2}{3}}{2}+9\frac{x^{\frac{5}{3}}}{5}-\\\\-\frac{3x^{\frac{8}{3}}}{8}+C \\ 5)\; \; \int e^{x}(1+\frac{e^{-x}}{cos^2x})dx=\int (e^{x}+\frac{1}{cos^2x})dx=e^{x}+tgx+C $$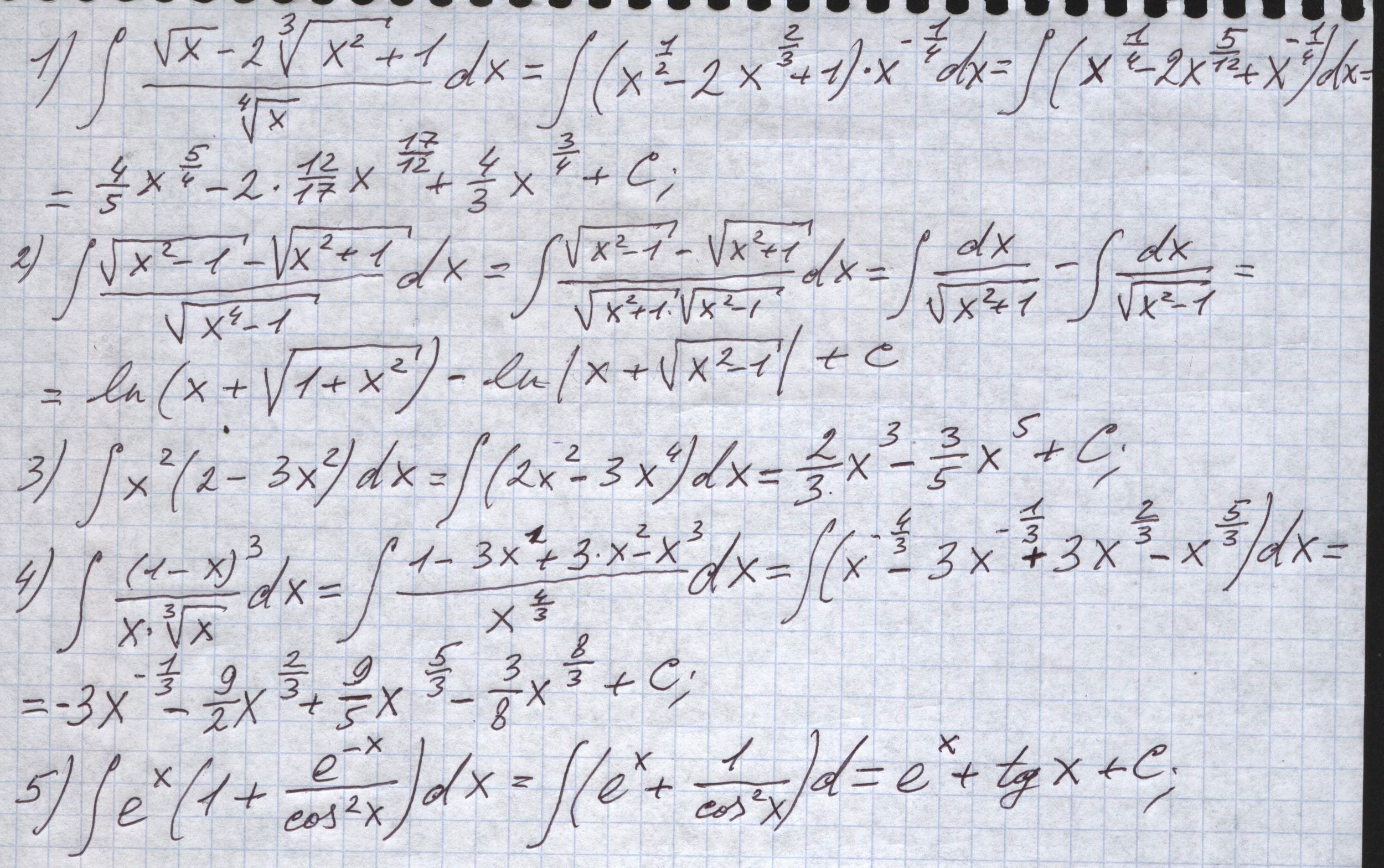

    int frac sqrt x - sqrt x sqrt x dx int x frac - x frac x - frac dx frac x frac - cdot frac x frac frac x frac C int frac sqrt x - - sqrt x sqrt x - dx int frac sqrt x - - sqr...

  • Вычислить интегралы, пользуясь формулой Ньютона-Лейбница. \( \int _0^1\frac{6x+5}{\sqrt{x^2-4x+8}}dx=\\ 2)\; \int _0^{\frac{\pi}{2}}(x-2)sin7x\, dx\\ 3)\; \int_1^2\frac{3x+5}{x(x^2-4x+8)}dx \)


    Решение: $$ \int _0^1\frac{6x+5}{\sqrt{x^2-4x+8}}dx=\int _0^1\frac{6x+5}{\sqrt{(x-2)^2+4}}dx=\\\\=[\, t=x-2,x=t+2,dx=dt,t_1=0-2=-2,t_2=1-2=-1\, ]=\\\\=\int _{-2}^{-1}\frac{6(t+2)+5}{\sqrt{t^2+4}}dt=\int _{-2}^{-1}\frac{6t+17}{\sqrt{t^2+4}}dt=3\cdot \int_{-2}^{-1}\frac{2t\cdot dt}{\sqrt{t^2+4}}+17\cdot \int _{-2}^{-1}\frac{dt}{\sqrt{t^2+4}}=\\\\=3\cdot 2\sqrt{t^2+4}|_{-2}^{-1}+17\cdot ln|t+\sqrt{t^2+4}||_{-2}^{-1}=\\\\=6(\sqrt5-\sqrt8)+17(ln(\sqrt3-1)-ln(\sqrt8-2)). \\ 2)\; \int _0^{\frac{\pi}{2}}(x-2)sin7x\, dx=[\, u=x-2,\; du=dx;\\\\ dv=sin7x\, dx,\; v=\int dv=-\frac{1}{7}cos7x\; ; \; \; \int u\cdot dv=uv-\int v\cdot du\, ]=\\\\=-\frac{1}{7}(x-2)cos7x|_0^\frac{\pi}{2}-\int _0^{\frac{\pi}{2}}(-\frac{1}{7})cos7x\, dx=\\\\=-\frac{1}{7}\cdot ((\frac{\pi}{2}-2)cos\frac{7\pi}{2}+2cos0)+\frac{1}{7}\cdot \frac{1}{7}sin7x|_0^{\frac{\pi}{2}}=[\, cos\frac{7\pi}{2}=0,cos0=1]\\\\=-\frac{1}{7}\cdot 2+\frac{1}{49}(sin\frac{7\pi}{2}-sin0)=[\, sin\frac{7\pi}{2}=-1,\; sin=0\, ]= \\ =-\frac{2}{7}-\frac{1}{49}=-\frac{15}{49}\\\\3)\; \int_1^2\frac{3x+5}{x(x^2-4x+8)}dx=I\\\\\frac{3x+5}{x(x^2-4x+8)}=\frac{A}{x}+\frac{Bx+C}{x^2-4x+8}=\frac{A(x^2-4x+8)+(Bx+C)\cdot x}{x(x^2-4x+8)}\\\\3x+5=Ax^2-4Ax+8A+Bx^2+Cx\\\\x^2\; \; |A+B=0\;,\; \; B=-A=-\frac{5}{8};\\\\x\; \; \; |-4A+C=3\;,\; \; C=3+4\cdot \frac{5}{8}=\frac{11}{2};\\\\x^0\; \; |8A=5\;,\; \; \; A=\frac{5}{8}. \\ I=\frac{5}{8}\int _1^2\frac{dx}{x}+\int_1^2\frac{-\frac{5}{8}x+\frac{11}{2}}{x^2-4x+8}\cdot \frac{-8}{-8}\cdot dx=ln|x||_1^2-\frac{1}{8}\int _1^2\frac{5x-44}{(x-2)^2+4}dx=\\\\=[\, t=x-2,x=t+2,dx=dt,t_1=-1,t_2=0\, ]=\\\\=ln2-ln1-\frac{1}{8}\int _{-1}^0\frac{5t-34}{t^2+4}dt=\\\\=ln2-\frac{1}{8}\cdot (\frac{5}{2}\int _{-1}^0\frac{d(t^2+4)}{t^2+4}-34\cdot 4\cdot \int _{-1}^0\frac{dt}{t^2+4} )=\\\\=ln2-\frac{5}{16}ln|t^2+4||_{-1}^0-17\cdot \frac{1}{2}arctg\frac{t}{2}|_{-1}^0=\\\\=ln2-\frac{5}{16}(ln4-ln5)- \\ -\frac{17}{2}(arctg0-arctg(-\frac{1}{2}))=ln2-\frac{5}{16}\cdot ln\frac{4}{5}-\frac{17}{2}arctg\frac{1}{2}. $$

<< < 161718 19 > >>