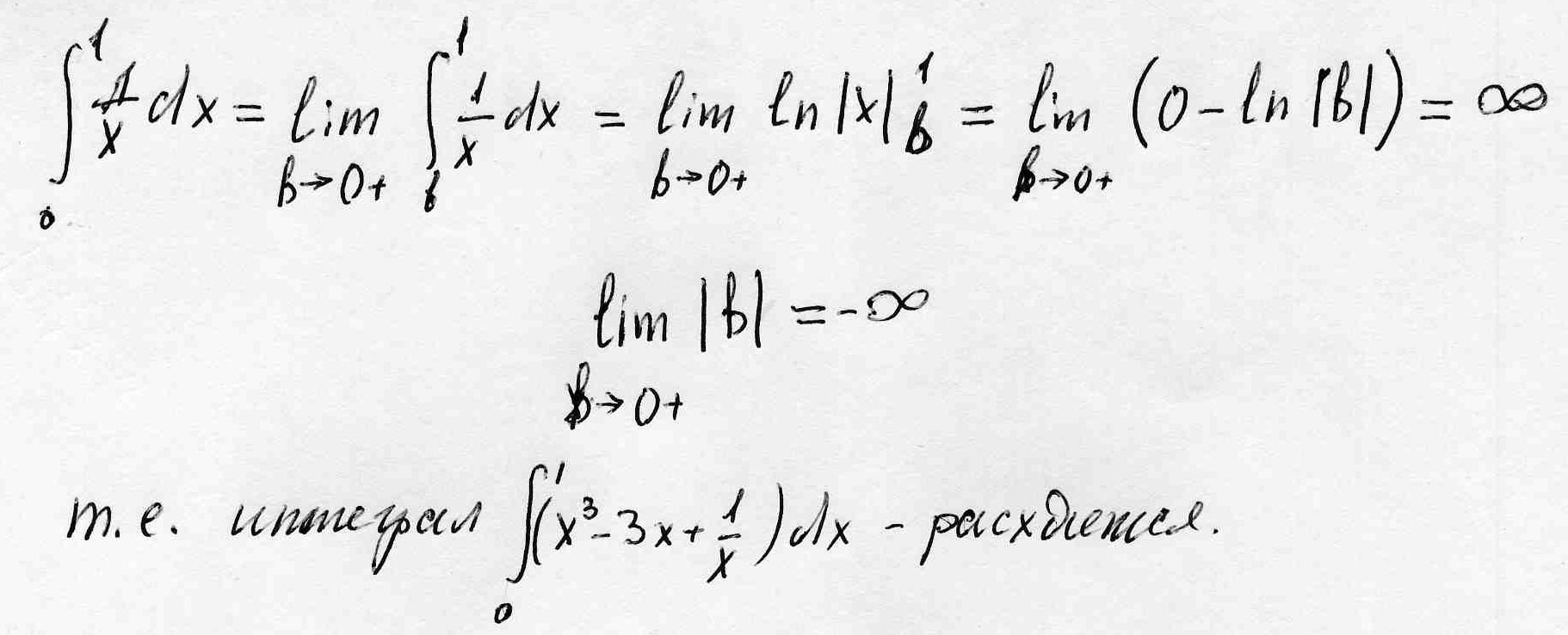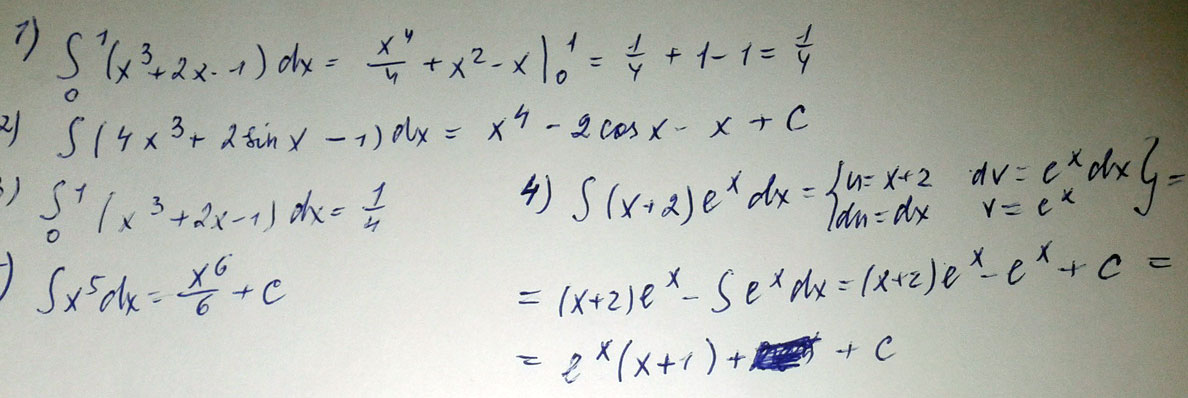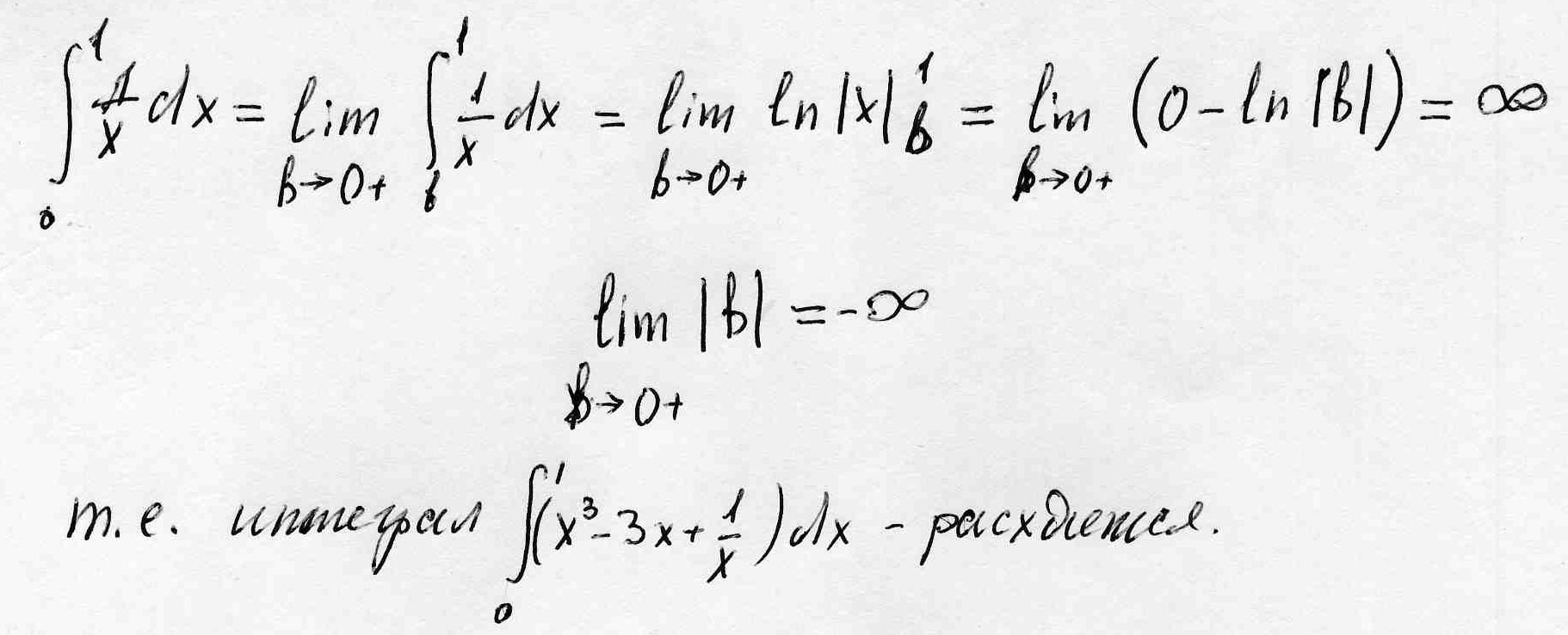интеграл »

вычислить интеграл - страница 16

  • Вычислить интеграл \( \int\limits^6_0 { \frac{5}{ \sqrt{0,5x+1} } } \, dx \)


    Решение: $$ \int\limits^6_0 { \frac{5}{ \sqrt{0,5x+1} } } \, dx = \int\limits^6_0 { \frac{5}{0,5 \sqrt{0,5x+1} } } \, d(0,5x+1) = \\ =10\int\limits^6_0 {(0,5x+1})^{-0.5} \, d(0,5x+1) = \\ =10* \frac{(0,5x+1)^{0.5}}{0.5} |_0^6=20( \sqrt{0.5*6+1} - \sqrt{0.5*0+1} )=20( \sqrt{4}- \sqrt{1})= \\ =20(2-1)=20 $$


    воспользуемся табличным интегралом:
    $$ \int\limits{x^n} \, dx =\int\limits\frac{x^{n+1}}{(n+1)} $$
    сперва возьмем этот интеграл:
    $$ \int\limits{\frac{5}{\sqrt{0.5x+1}}} \, dx $$
    вынесем 5 из под знака интеграла и сделаем замену: $$ 0.5x+1=u $$
    возьмем производную для нашей замены:
    $$ du=\frac{1}{2}dx, dx=2du $$
    подставим:
    $$ 5\int\limits {\frac{2du}{\sqrt{u}}}=10\int\limits u^{-\frac{1}{2}du}=10\frac{u^{\frac{1}{2}}}{\frac{1}{2}}=20\sqrt{u}=20\sqrt{0.5x+1} $$
    теперь найдем определенный интеграл:
    $$ \int\limits^6_0 \frac{5dx}{\sqrt{0.5x+1}}=20\sqrt{0.5x+1}|^6_0=20\sqrt{4}-20*\sqrt{0+1}=20 $$

  • Вычислить интеграл \(\int\limits_0^1(x^3+2x-1)dx \)


    Решение: 1) $$ \int\limits^1_0 { x^{3}+2x-1 } \, dx= \frac{ x^{4} }{4} + x^{2} -x= \frac{1}{4}+1-1= \frac{1}{4} $$
    2) $$ \int\limits^-_- {4 x^{3}+2sinx-1 } \, dx = x^{4}-2cosx - x+const $$
    3) $$ \int\limits^-_- {(x+2) e^{x} } \, dx =(x+1) e^{x}+const $$
    4) $$ \int\limits^-_- { x^{5} } \, dx = \frac{ x^{6} }{6} + const $$

    ////////////////////////////////////////////

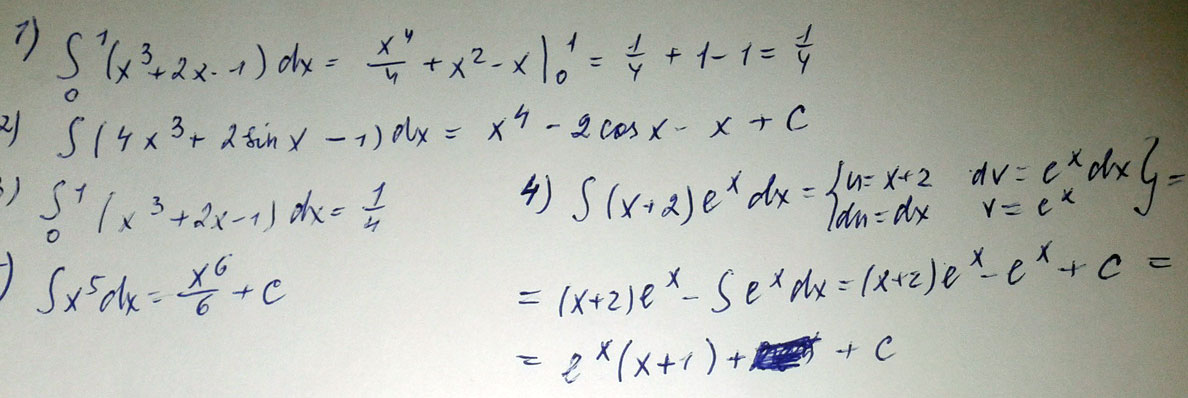
      int limits x x- dx frac x x -x frac - frac   int limits - - x sinx- dx x - cosx - x const   int limits - - x e x dx x e x const   int limits - - x dx frac x const...

  • Вычислить интеграл: \(\int\limits_0^{\frac{\pi}{2}}sinx cosx dx \)


    Решение: ∫₀ sinxcosx dx=∫₀ (1/2* sin2x) dx=1/2*( -1/2cos2x) |₀= -1/4(cosπ-cos0)= -1/4(-1-1)=1/2

    Воспользовались формулой sin2x=2sinxcosx

    $$ \int\limits_0^{\pi/2}{sinx*cosx}dx=\frac{1}{2}\int\limits_0^{\pi/2}{2sinx*cosx}dx= \frac{1}{2}\int\limits_0^{\pi/2}{sin2x}dx= \\ \\ =\frac{1}{2}*(-\frac{1}{2}*cos2x)[_0^{\pi/2}= -\frac{1}{4}*cos2x[_0^{\pi/2}= \\ \\ =-\frac{1}{4}*cos{(2*\frac{\pi}{2})}-(-\frac{1}{4}*cos0)= -\frac{1}{4}*(-1)+\frac{1}{4}*1= \\ \\ =\frac{1}{4}+\frac{1}{4}=\frac{1}{2}=0,5 $$

  • Вычислить интеграл
    dx/(4x^2+3)


    Решение: Обозначу интеграл как Int. А вы поставьте обычный знак "интеграл".
    Int 1/(4x^2+3)*dx = 1/3 Int(1/(4x^2/3 + 1)
    Введем u=2x√3/3 du=2√3/3 *dx и подставим √3/2 du
    имеем Int √3/(2u^2+2) *du = √3/2 Int 1/(u^2+1)du = √3/2 * арктангенс (u)
    подставим u и получим √3/6* арктангенс (2х√3/3)+С Это ответ.

  • Вычислить интеграл: \( \int\limits_0^1 (x^3-3+\frac{1}{x})dx \)


    Решение: Это несобственный интеграл. В точке 0. подинтегральная функция

    терпит разрыв. решение разбивается на два интеграла.

    первый дает

    x^4/4-3x|1-0=1/4-3-0-0=-2,75

    второй интеграл расходится, следовательно расходится

    и основной инетеграл.

    Это несобственный интеграл. В точке . подинтегральная функция терпит разрыв. решение разбивается на два интеграла. первый дает x - x - - - - - второй интеграл расходится след...
<< < 141516 17 18 > >>