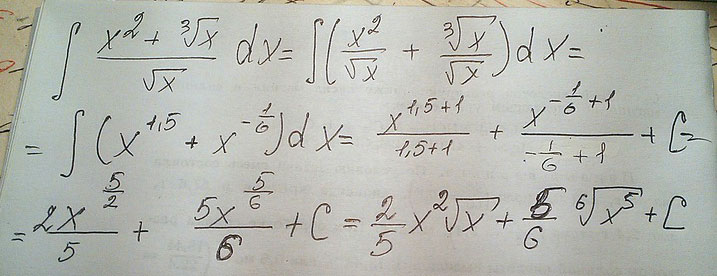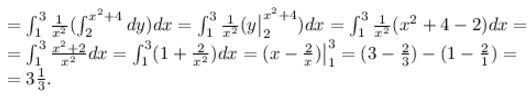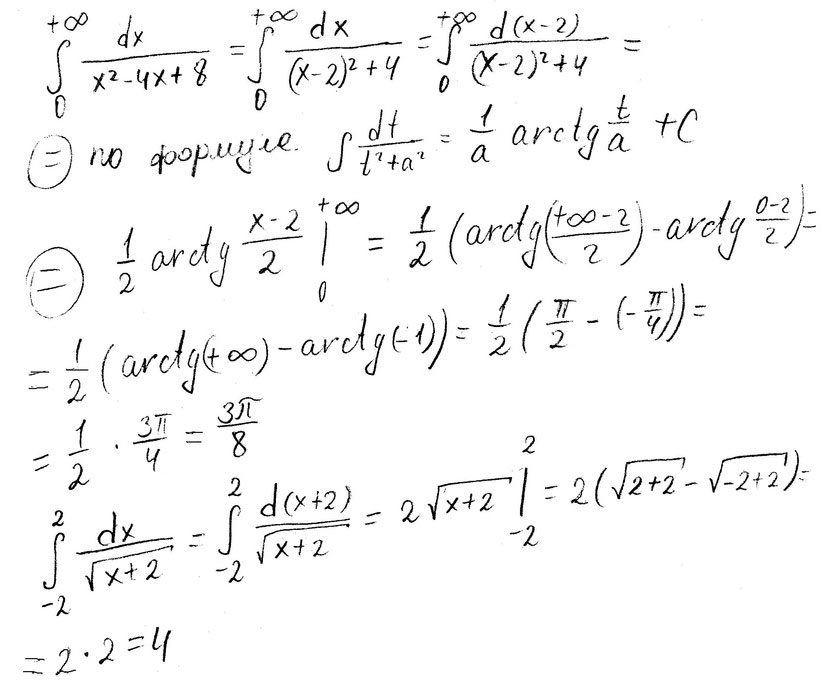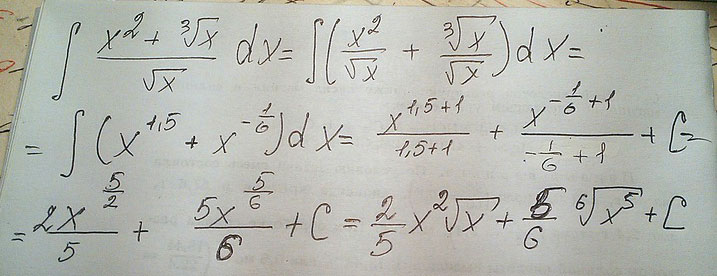интеграл »
вычислить интеграл - страница 15
Вычислить интеграл, пользуясь формулой Ньютона-Лейбница (подробно)
\( \int\limits^1_02 x+1/ \sqrt{x^2+2x+2} \, dx \)
Решение: Формулы:
$$ 1) \int\limits { \frac{du}{ \sqrt{u} } } \, dx =2 \sqrt{u} +C \\ \\ 2)\int\limits { \frac{du}{ \sqrt{u^2+k} } } \, dx =ln|u+\sqrt{u^2+k} |+C \\ \int\limits { \frac{2x+1}{ \sqrt{ x^{2} +2x+2} } } \, dx = \int\limits { \frac{2x+2-1}{ \sqrt{ x^{2} +2x+2} } } \\ dx=\int\limits {( \frac{2x+2}{ \sqrt{ x^{2} +2x+2} } } \, \ - \frac{1}{ \sqrt{ x^{2} +2x+2} })dx = \\ \\ \int\limits { \frac{2x+2}{ \sqrt{ x^{2} +2x+2} } } \,dx \ - \int\limits \frac{1}{ \sqrt{ x^{2} +2x+2} }\, dx. \\ 1) \ \int\limits { \frac{2x+2}{ \sqrt{ x^{2} +2x+2} } } \,dx \\ \\ \sqrt{u} = \sqrt{ x^{2} +2x+2} \\ du=(x^{2} +2x+2)’=2x+2 $$
Подходит первая формула:
$$ \ \int\limits { \frac{2x+2}{ \sqrt{ x^{2} +2x+2} } } \,dx=2\sqrt{ x^{2} +2x+2}+C \\ 2)\int\limits \frac{1}{ \sqrt{ x^{2} +2x+2} }\, dx=\int\limits \frac{1}{ \sqrt{ x^{2} +2x+1+1} }\, dx=\int\limits \frac{1}{ \sqrt{ (x+1)^2+1} }\, dx \\ u=x+1 \\ du=(x+1)’=1 \\ $$
Подходит вторая формула:
$$ \int\limits {\frac{1}{ \sqrt{ (x+1)^2+1} } }\, dx =ln|x+1+\sqrt{ (x+1)^2+1}|+C \\ \int\limits^1_0 { \frac{2x+1}{ \sqrt{ x^{2} +2x+2} } } \, dx = 2\sqrt{ x^{2} +2x+2} \ -ln|x+1+\sqrt{ (x+1)^2+1}|\ \ |^1_0 \\ \\ 2\sqrt{ 1^{2} +2*1+2} \ -ln|1+1+\sqrt{ (1+1)^2+1}| - \\ \\ -( 2\sqrt{ 0^{2} +2*0+2} \ -ln|0+1+\sqrt{ (0+1)^2+1}|)= \\ \\ 2 \sqrt{5} -ln|2+ \sqrt{5} |-(2 \sqrt{2} -ln|1+ \sqrt{2} |)= \\ \\ 2 \sqrt{5} -ln(2+ \sqrt{5} )-2 \sqrt{2}+ln(1+ \sqrt{2} )=2( \sqrt{5} - \sqrt{2} )+ln \frac{1+ \sqrt{2} }{2+ \sqrt{5} } $$
Вычислите повторный интеграл \(\int\limits_1^3 dx \int\limits_2^{x^2 +4} \frac{1}{x^2}dy \)
Решение: $$ = \int _1^3 \frac{1}{x^2} (\int_{2}^{x^2+4}dy)dx= \int _1^3 \frac{1}{x^2} (y \big|_{2}^{x^2+4})dx= \int _1^3 \frac{1}{x^2} (x^2+4-2)dx=\\ = \int _1^3 \frac{x^2+2}{x^2} dx=\int _1^3 (1+\frac{2}{x^2}) dx= (x- \frac{2}{x}) \big|_1^3= (3- \frac{2}{3})-(1- \frac{2}{1})= \\ =3 \frac{1}{3}. $$ Так как верхний предел второго вложенного интеграла зависит от икса ($$ x^{2} +4 $$), то порядок интегрирования важен и нужно брать со второго интеграла. Во вложении решение прилагается.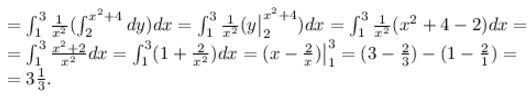
Вычислить интеграл и проверить результат, исходя из его геометрического смысла \( \int\limits^2_1 {(4-2x)} \, dx \)
Решение: $$ \int\limits^2_1 {(4-2x)} \, dx=(4x-x^{2})|_{1}^{2}=4*2-2^2-4*1+1^2=1 $$
Геометрический смысл интеграла это площадь некоторой фигуры. В приведённом примере фигура ограничена прямой у=4-2х, осью ОХ и линией х=1, эта фигура - прямоугольный треугольник площадь которого 1ед² мы нашли вычислив интеграл.
Площадь прямоугольного треугольника равна половине произведения катетов. Из рисунка находим длину катетов 2 ед. и 1 ед. найдём площадь:
S=(1/2)*2*1=1 ед²
Что и требовалось доказать.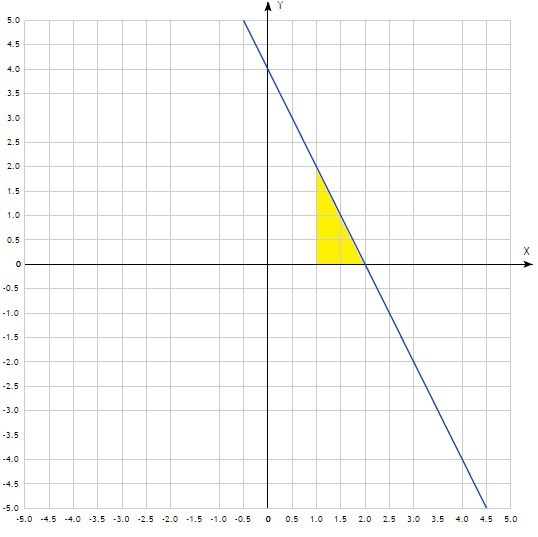
Вычислить интеграл или установить его расходимость ∫dx/(x²-4x+8)
Решение: 1) ∫dx/(x²-4x+8)=∫dx/((x-2)²+4)=∫d(x-2)/((x-2)²+2²)=1/2*arctg((x-2)/2). При x⇒+∞ lim 1/2*arctg((x-2)/2)=1/2*π/2=π/4, при x=0 1/2*arctg((x-2)/2)=1/2*(-π/4)=-π/8. Значит, интеграл сходится и равен π/4-(-π/8)=3*π/8.
Ответ: 3*π/8.
2) Здесь подынтегральная функция терпит разрыв при x=-2. Поэтому после нахождения первообразной вместо подстановки значения x=-2 придётся подставить вместо x число -2+e=e-2 (e - сколь угодно малое положительное число) рассмотреть предел при e⇒0. ∫dx/√(x+2)=∫d(x+2)/√(x+2)=2*√(x+2). При x=2 2*√(2+2)=4, а lim 2*√(e-2+2) при e⇒0=2*√e=0. Интеграл сходится и равен 4-0=4. Ответ: 4.
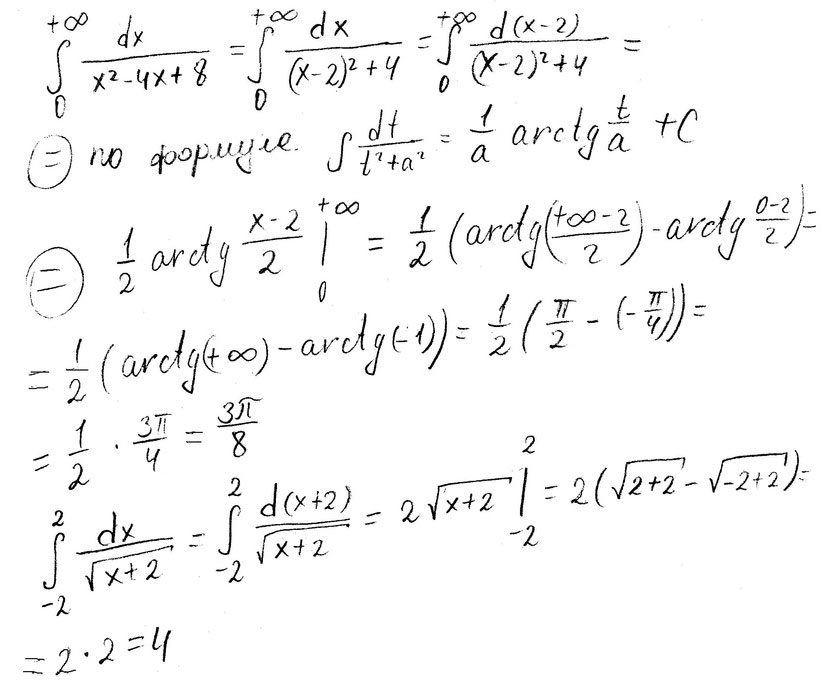
Вычислить интеграл и его приложение \( \int(\frac{x^2+\sqrt[3]{x}}{\sqrt x})dx \)
Решение:$$ \int\ {(x^{ \frac{2}{3} }+x^{- \frac{1}{6} })} \, dx = \frac{x^ \frac{5}{2} }{ \frac{5}{2} }+ \frac{x^ \frac{5}{6} }{ \frac{5}{6} }= \frac{2}{5}x^ \frac{5}{2}+ \frac{6}{5}x^ \frac{5}{6} +C $$