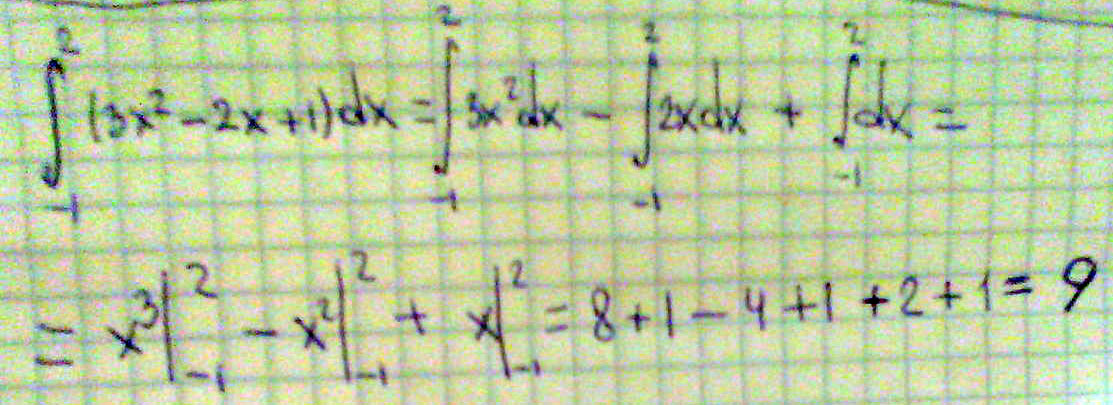вычислить интеграл - страница 13
Вычислить интеграл |8cos(4x-12)dx
Решение: $$ \int{8cos(4x-12)}\, dx $$выносим константу за знак интеграла
$$ 8\int{cos(4x-12)}\, dx $$
проведем замену переменной
$$ u=4x-12 \\ 8\int{\frac{1}{4}cos(u)}\, du $$
выносим константу за знак интеграла
$$ 2\int{cos(u)}\, du $$
проинтегрируем косинус
$$ 2sin(u) $$
проведем обратную замену переменной
$$ 2sin(4x-12) $$
запишем конечный результат
$$ \int{8cos(4x-12)}\, dx=2sin(4x-12)+const $$
вычислить интеграл: \(\int\limits_{-1}^2 (3х^2 -2х+1)dx\)
Решение: Находим первообразную без прибавления константы, то есть без +Сx^3 - x^2 + x
И находим разность между подставленными в выражение выше 2 и -1
(2^3-2^2+2) - ((-1)^3-(-1)^2-1)=(8-4+2)-(-1-1-1)=6+3=9
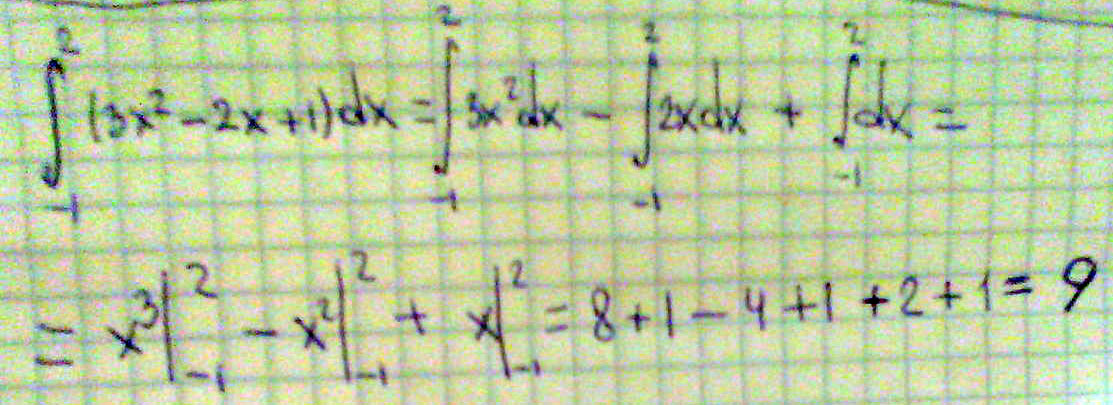
Найти интеграл \( \int\limits^{3}_{0} ln(x + 3) \ dx \) интегрирование по частям
Решение: dx=dv ln(x+3)=u v=x du=1/(x+3)*dxuv-интеграл(v*du)=xln(x+3)-инт(0,3)(x/(x+3)*dx) = xln(x+3)-инт((x+3-3)/(x+3)) = xln(x+3)-инт(1-3/(x+3)) = xln(x+3)-x+ln(x+3) = 3ln6-6+ln6-ln3 = 7ln6+ln3-6
$$ \int\limits^{3}_{0} ln(x + 3) \ dx = F(3) - F(0) \\ [ \ \int ln(x + 3) \ dx = xln(x + 3) - \int \frac{x}{x+3} \ dx =\\\\ xln(x + 3) - \int \frac{x + 3 - 3}{x+3} \ dx = xln(x + 3) - \int 1 - \frac{3}{x+3} \ dx =\\\\ xln(x + 3) - x + 3ln(x + 3) + C = (x+3)ln(x + 3) - x + C\ ] \\ F(3) - F(0) = (x+3)ln(x + 3) - x | \int\limits^{3}_{0}= 6ln6 - 3 -3ln3 =\\\\ 3(2ln6 - ln3) - 3 = 3(ln6^2 - ln3) - 3 =3ln12 - 3 = 3(ln12 - 1) $$
Вычислить интеграл, преобразуя по формуле 1/2[cos(a+b)+cos(a-b)]
интеграл от внизу П/2 до П cosxcos2xdx
Решение: $$ \int\limits^ \pi _ { \pi /2} {(\cos x\cos2x) } \, dx= \int\limits^ \pi _ { \pi /2} {( \frac{1}{2} (\cos (x+2x)+\cos(x-2x) ))} \, dx \\\ =\frac{1}{2} \int\limits^ \pi _ { \pi /2} { (\cos 3x+\cos x}) \, dx=\frac{1}{2}(\sin3x\cdot \frac{1}{3}+\sin x )|^ \pi _ { \pi /2}= \\\ =(\frac{1}{6}\sin3x+\frac{1}{2}\sin x )|^ \pi _ { \pi /2}= \frac{1}{6}\sin3 \pi+\frac{1}{2}\sin \pi -\frac{1}{6}\sin \frac{3 \pi }{2} -\frac{1}{2}\sin \frac{ \pi }{2}= \\\ =0+0-\frac{1}{6}\cdot(-1)- \frac{1}{2} \cdot1=-\frac{1}{3} $$Вычислить интеграл (sin^2) x на промежутке (0;pi/2).
Решение: $$ \int\limits^{ \frac{ \pi}{2} }_0 {sin^2x} \, dx $$
Воспользуемся формулой
1-cos2x=2sin²x
sin²x=1/2-(1/2)cos2x
$$ \int\limits {( \frac{1}{2}- \frac{1}{2}cos2x) } \, dx= \frac{x}{2}- \frac{1}{2} \int\limits{cos2x} \, dx= $$
Вводим замену переменной
2x=u, тогда du=2dx ⇒ dx=du/2
$$ =\frac{x}{2}- \frac{1}{4} \int\limits{cosu}\, du=\frac{x}{2}- \frac{1}{4}sinu=\frac{x}{2}- \frac{1}{4}sin2x+C \\ \int\limits^{ \frac{ \pi}{2} }_0 {sin^2x} \, dx=\frac{x}{2}- \frac{1}{4}sin2x|_0^{ \frac{ \pi }{2}} = \frac{ \pi }{4} - \frac{1}{4}sin \pi -0+0= \frac{ \pi }{4}-0= \frac{ \pi }{4} $$