интеграл »

вычислить интеграл - страница 12

  • Вычислить интеграл (с проверкой):
    \( \int\sqrt{2-x-x^{2}} \)


    Решение: Воспользуемся формулой
    $$ \int\sqrt{a^2-t^2}dt=\frac{t}{2}\sqrt{a^2-t^2}+\frac{a^2}{2}\arcsin(\frac{t}{a})+C $$
    Теперь сам интеграл следует привести к этому виду
    $$ \int\sqrt{2-x-x^2}dx=\int\sqrt{2+0,25-0,25-x-x^2}dx= \\ =\int\sqrt{2,25-(0,25+x+x^2)}dx=\int\sqrt{2,25-(0,5+x)^2)}dx= \\ =\int\sqrt{2,25-(0,5+x)^2)}d(x+0,5) $$
    Замена t=x+0,5.
    $$ \int\sqrt{2,25-t^2}dt=\int\sqrt{1,5^2-t^2}dt=\frac{t}{2}\sqrt{2,25-t^2}+\frac{2,25}{2}\arcsin\frac{t}{1,5}+C $$
    Теперь подставим вместо t его значение (x+0,5).
    $$ =\frac{x+0,5}{2}\sqrt{2,25-(x+0,5)^2}+\frac{2,25}{2}\arcsin(\frac{x+0,5}{1,5})+C= \\ =\frac{x+0,5}{2}\sqrt{2-x-x^2}+\frac{9}{8}\arcsin(\frac{2*(x+0,5)}{3})+C= $$ 
    $$ =\frac{x+0,5}{2}\sqrt{2-x-x^2}+\frac{9}{8}\arcsin(\frac{2x+1}{3})+C= \\ =\frac{2x+1}{4}\sqrt{2-x-x^2}+\frac{9}{8}\arcsin(\frac{2x+1}{3})+C= $$
    Проверка во вложении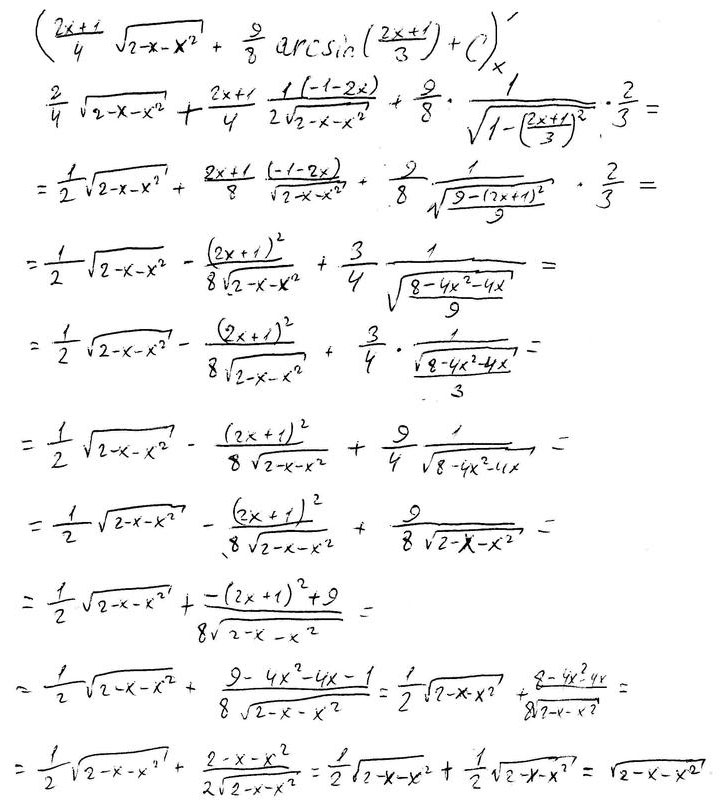

    Воспользуемся формулой int sqrt a -t dt frac t sqrt a -t frac a arcsin frac t a C Теперь сам интеграл следует привести к этому виду int sqrt -x-x dx int sqrt - -x-x dx int sq...

  • Вычислить интеграл: \( \int \limits_{\frac{\pi}{18}}^{\frac{\pi}{4}} {\cos 4x}\, dx= \)


    Решение: $$ \\\int \limits_{\frac{\pi}{18}}^{\frac{\pi}{4}} {\cos 4x}\, dx=(*)\\ t=4x\\ dt=4\, dx\\ \int \limits_{\frac{\pi}{18}}^{\frac{\pi}{4}} \frac{1}{4}{\cos t}\, dt=\\ \frac{1}{4}\int \limits_{\frac{\pi}{18}}^{\frac{\pi}{4}} {\cos t}\, dt=\\ \frac{1}{4}\Big[\sin t\Big]_{\frac{\pi}{18}}^{\frac{\pi}{4}}=\\ (*)=\frac{1}{4}\Big[\sin 4x\Big]_{\frac{\pi}{18}}^{\frac{\pi}{4}}=\\ \frac{1}{4}(\sin (4\cdot\frac{\pi}{4})-\sin (4\cdot\frac{\pi}{18}))=\\\frac{1}{4}(\sin \pi-\sin \frac{2\pi}{9})=\\\frac{1}{4}(0-\sin \frac{2\pi}{9})=\\-\frac{1}{4}\sin \frac{2\pi}{9}\approx-0,16\\ $$

  • вычислить интеграл:

    ∫от π/8 до π/4 cos4xdx


    Решение: = sin4x/4 |от пи/8 до пи/4 = 1/4 * (sin4*pi/4 - sin 4*pi/8) = 1/4 *(sinpi-sin(pi/2)) = 1/4*(0-1) = -1/4

    $$ \\\int \limits_{\frac{\pi}{8}}^{\frac{\pi}{4}} {\cos 4x}\, dx=(*)\\ t=4x\\ dt=4\, dx\\ \int \limits_{\frac{\pi}{8}}^{\frac{\pi}{4}} \frac{1}{4}{\cos t}\, dt=\\ \frac{1}{4}\int \limits_{\frac{\pi}{8}}^{\frac{\pi}{4}} {\cos t}\, dt=\\ \frac{1}{4}\Big[\sin t\Big]_{\frac{\pi}{8}}^{\frac{\pi}{4}}=\\ (*)=\frac{1}{4}\Big[\sin 4x\Big]_{\frac{\pi}{8}}^{\frac{\pi}{4}}=\\ \frac{1}{4}(\sin (4\cdot\frac{\pi}{4})-\sin (4\cdot\frac{\pi}{8}))=\\ \frac{1}{4}(\sin \pi-\sin \frac{\pi}{2})=\\ \frac{1}{4}(0-1)=\\ \frac{1}{4}\cdot(-1)=\\ -\frac{1}{4} $$

  • вычислить интеграл:

    ∫от 0до 1(2x+3)³dx


    Решение: $$ \\\int\limits_0^1{(2x+3)^3}\, dx=(*)\\ t=2x+3\\ dt=2\,dx \\ \int\limits_0^1{\frac{1}{2}t^3}\, dt=\\ \frac{1}{2}\int\limits_0^1{t^3}\, dt=\\ \frac{1}{2}\Big[\frac{t^4}{4}\Big]_0^1\\ (*)=\frac{1}{2}\Big[\frac{(2x+3)^4}{4}\Big]_0^1=\\ \frac{1}{2}\cdot\frac{(2\cdot1+3)^4}{4}-\frac{1}{2}\cdot \frac{(2\cdot0+3)^4}{4}=\\ \frac{1}{2}\cdot\frac{5^4}{4}-\frac{1}{2}\cdot \frac{3^4}{4}=\\ \frac{1}{2}\cdot\frac{625}{4}-\frac{1}{2}\cdot \frac{81}{4}=\\ \frac{625}{8}-\frac{81}{8}=\\ \frac{544}{8}=\\ 68 $$

  • Вычислите интеграл
    \( \int\limits^ \frac{ \pi }{2} _ {0} \, \frac{cosdx}{2sinx+1} \)


    Решение: Заметим, что подынтегральная функция нигде в промежутке$$ [0,\frac{\pi}{2}] $$ не обращается в ∞. То есть подынтегральная функция интегрируема по Риману в данном промежутке.
    $$ \cos x\,dx=d(\sin x) \\ \int_0^\frac{\pi}{2}\frac{\cos x\,dx}{2\sin x+1}=\int_0^\frac{\pi}{2}\frac{d\sin x}{2\sin x+1}= \\ =\int_0^\frac{\pi}{2}\frac{\frac{1}{2}d(2\sin x)}{2\sin x+1}=\frac{1}{2}\int_0^\frac{\pi}{2}\frac{d(2\sin x)}{2\sin x+1}=\frac{1}{2}\int_0^\frac{\pi}{2}\frac{d(2\sin x+1)}{2\sin x+1}= $$
    Можно заметить, что подынтегральная функция теперь имеет вид:
    $$ \int\frac{dt}{t}=\ln|t| $$
    Получается, что
    $$ =\frac{1}{2}\ln(2\sin x+1)|_0^\frac{\pi}{2}=\frac{1}{2}(\ln|2\sin\frac{\pi}{2}+1|-\ln|2\sin 0+1|)= \\ =\frac{1}{2}(\ln|3|-\ln|1|)=\frac{\ln 3}{2} $$
    Ответ: $$ \frac{\ln 3}{2} $$

<< < 101112 13 14 > >>