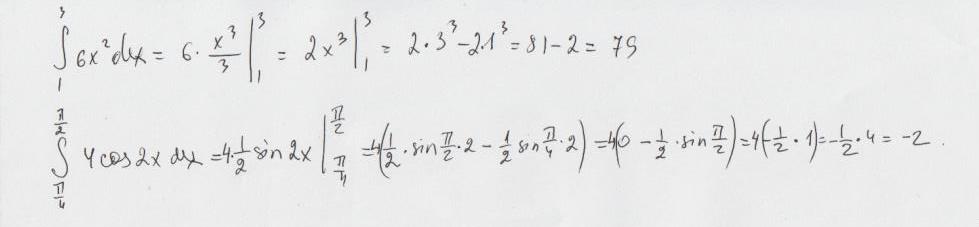интеграл »

вычислить интеграл - страница 10

  • Вычислить интеграл методом постановки [ dx/ (1+e^x)


    Решение: Заменим: e^x=u, значит e^x *dx = du, получаем
    $$ \int\limits { \frac{1}{u(u+1)} } \, du= \int\limits { \frac{A}{u} } \, du + \int\limits { \frac{B}{u-1} } \, du \boxed{=}\\ \frac{1}{(u+1)u}= \frac{A}{u}+ \frac{B}{u+1}= \frac{A(u+1)+Bu}{u(u+1)} \\x^0:\,\,\,1=A\\x^{-1}:\,\,\,B=-1\\\boxed{=} \int\limits { \frac{1}{u} } \, du - \int\limits { \frac{1}{u+1} } \, du=\ln|u|-\ln|u+1|+C=\\=\ln |\frac{u}{u+1}|+C=\ln| \frac{e^x}{e^x+1} |+C= \ln \frac{e^x}{e^x+1}+C $$

  • Вычислите интеграл : а) интеграл от 0,25 до 0, 5 dx/x^2
    б) Вычислить интеграл от 0 до пи / 4 cos2xdx


    Решение: А) $$ \int\limits^a_b {1/x^2} \, dx $$
    тогда первообразная $$ -1/x $$
    вычтем из полученного значения для верхнего предела, полученное значение для нижнего предела: - 2 - ( - 4) = 2
    Ответ: а) 2 
    б) $$ \int\limits^a_b {cos(2x)} \, dx $$
    тогда первообразная $$ 1/2 * sin(2x) $$
    вычтем из полученного значения для верхнего предела, полученное значение для нижнего предела: 1/2 * sin(pi/2) - 1/2 * sin(0) = 1/2
    Ответ: б) 1/2

  • Вычислить интеграл:
    1) cos^3(x)*sin^2(x) dx
    2)dx\(x^2+10x-1)


    Решение: $$ 1)\; \int cos^3x\cdot sin^2x\, dx=\int sin^2x\cdot cos^2x\cdot cosx\, dx=\\\\=\int sin^2x(1-sin^2x)cosx\, dx=[\, t=sinx,\; dt=cosx\, dx\, ]=\\\\=\int (t^2-t^4)dt=\frac{t^3}{3}-\frac{t^5}{5}+C=\frac{1}{3}sin^3x-\frac{1}{5}sin^5x+C \\ 2)\; \; \int \frac{dx}{x^2+10x-1}=\int \frac{dx}{(x+5)^2-26}=[\, t=x+5,\; dt=dx\, ]=\\\\=\int \frac{dt}{t^2-26}=\frac{1}{2\sqrt{26}}\cdot ln\left |\frac{t-\sqrt{26}}{t+\sqrt{26}}\right |+C=\frac{1}{2\sqrt{26}}\cdot ln\left |\frac{x+5\sqrt{26}}{x+5+\sqrt{26}}\right |+C $$

  • Вычислите интеграл. Объясните поэтапно, как это решить.
    \( \int\limits^1_3 6 x^{2} \, dx \)
    \( \int\limits^ \frac{ \pi }{2} _ \frac{ \pi }{4} 4cos2{x} \, dx \)


    Решение:

    $$ \int\limits^1_3 {6x^2} \, dx = $$ {Первообразная произведения числа 6 на функцию $$ x^{2} $$ равна произведению числа 6 на первообразную функции  $$ x^{2} $$, получаем}
    $$ =6* \frac{x^3}{3} \mid ^1_3 =2 x^{3} \mid ^1_3= $$ {первообразную функции  $$ x^{2} $$, получили по формуле "первообразная степенной функции", далее по формуле Ньютона-Лейбница $$ \int\limits^b_a {x} \, dx =F(b)-F(a) $$ получаем}
    $$ =2*1^3-2*3^3=2-54=-52 \\ \int\limits^ \frac{ \pi }{2} _ \frac{ \pi }{4} {4cos2x} \, dx = $${Первообразная произведения числа 4 на функцию $$ cos2x $$ равна произведению числа 4 на первообразную cложной функции  $$ cos2x $$ с коэффициентом $$ \frac{1}{2} $$, получаем}
    $$ =4* \frac{1}{2}sin2x \mid ^ \frac{ \pi }{2} _\frac{ \pi }{4}=2sin2x \mid ^ \frac{ \pi }{2} _ \frac{ \pi }{4}= $$ {первообразную функции  $$ cos2x $$, получили по формуле "первообразная тригонометрической функции", далее по формуле Ньютона-Лейбница $$ \int\limits^b_a {x} \, dx =F(b)-F(a) $$ получаем}
    $$ =2sin(2*\frac{ \pi }{2})-2sin(2* \frac{ \pi }{4})=2sin \pi - 2sin( \frac{ \pi }{2}) =-2 $$

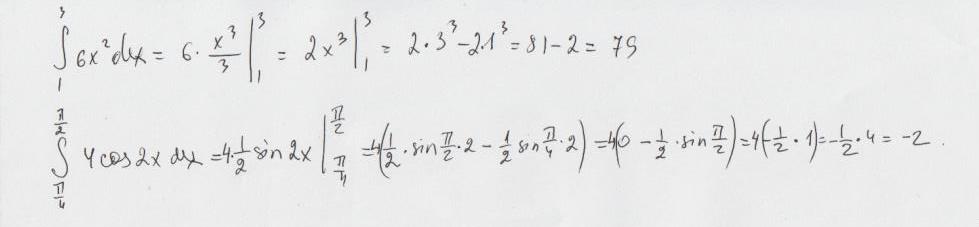
    int limits x dx   Первообразная произведения числа на функцию  x равна произведению числа на первообразную функции   x получаем frac x mid x mid   первообразную функции   x п...

  • Вычислить интеграл, выделив целую часть дроби (применяя деление «уголком» многочлена на многочлен) и разложив интеграл на сумму более простых интегралов. \( \int\limits { \frac{x^5+2}{x^2-4} } \, dx \)


    Решение: _  x⁵ + 2  | x²-4
        x⁵- 4x³  x³+4x
       -
       _ 4x³+2
       4x³-16x
       -
       16x +2
      
    (x⁵+2)/(x²-4)=x³+4x + (16x+2/(x²-4))
    $$ \int\limits { \frac{x^5+2}{x^2-4} } \, dx= \int\limits (x^3+4x+ \frac{16x+2}{x^2-4})dx= \\ \\ = \int\limits (x^3+4x+8\cdot \frac{2x}{x^2-4}+ \frac{1}{2(x-2)}- \frac{1}{2(x+2)} )dx= \\ \\ == \frac{x^4}{4}+2x^2+8ln|x^2-4|+ \frac{1}{2} ln|x-2|- \frac{1}{2}ln|x+2|+C. $$

<< < 8910 11 12 > >>