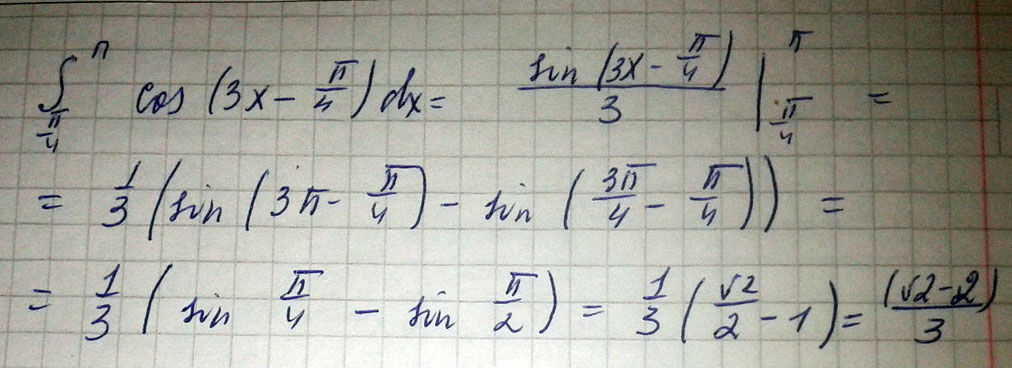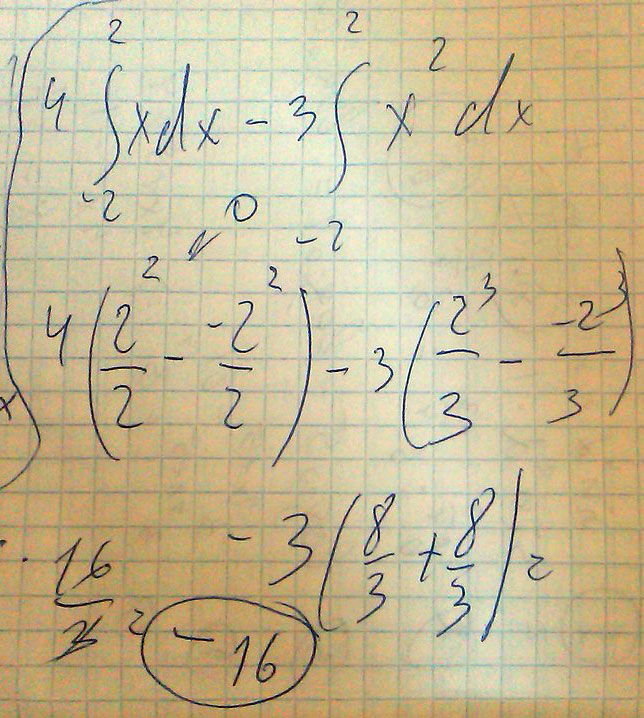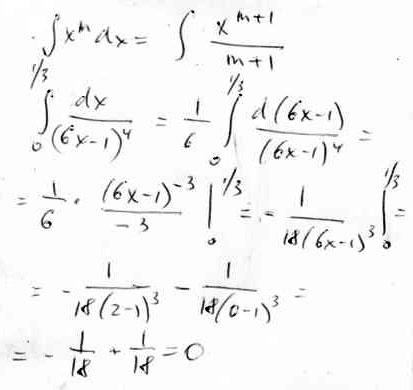интеграл »

вычислить интеграл - страница 11

  • Вычислите интеграл (2-9x)^6*dx


    Решение: 1/(x^2 + 9x) = 1/x(x+9)
    Разделяете дробь методом неопределенных коэффициентов:
    1/x(x+9) = A/x + B/(x + 9)
    Получившиеся интегралы табличные - ищете в таблице интегралов элементарных функций.

  • Вычислите интеграл \( \int\limits^ \pi _ \frac{ \pi }{4} {cos(3x- \frac{ \pi }{4} } )\, dx \)


    Решение: $$ \int\limits^ \pi _ \frac{ \pi }{4} {cos(3x- \frac{ \pi }{4} } )\, dx =- \frac{1}{3} cos(3x+ \frac{ \pi }{4} )= \\ - \frac{1}{3} cos(3 \pi + \frac{ \pi }{4} )-(- \frac{1}{3} cos( \frac{3 \pi }{4} + \frac{ \pi }{4}))=- \frac{1}{3} ( -\frac{ \sqrt{2} }{2} +1) $$

    ////////////////////////////////////////////////////////////

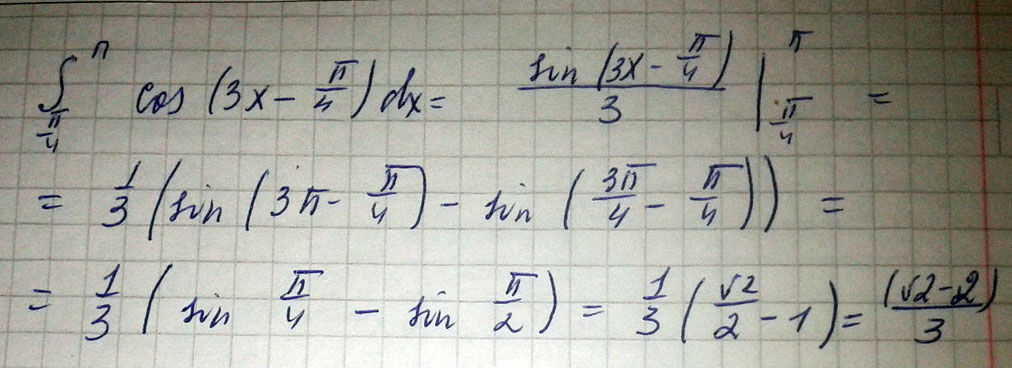
    int limits pi frac pi cos x- frac pi dx - frac cos x frac pi - frac cos pi frac pi - - frac cos frac pi frac pi - frac - frac sqrt...

  • Вычислите интеграл \( \int _{-2}^2(4x-3x^2)dx\)


    Решение: $$ \int _{-2}^2(4x-3x^2)dx=(4\frac{x^2}{2}-3\frac{x^3}{3})|_{-2}^2=(2x^2-x^3)|_{-2}^2=\\\\=8-8-(8+8)=-16 $$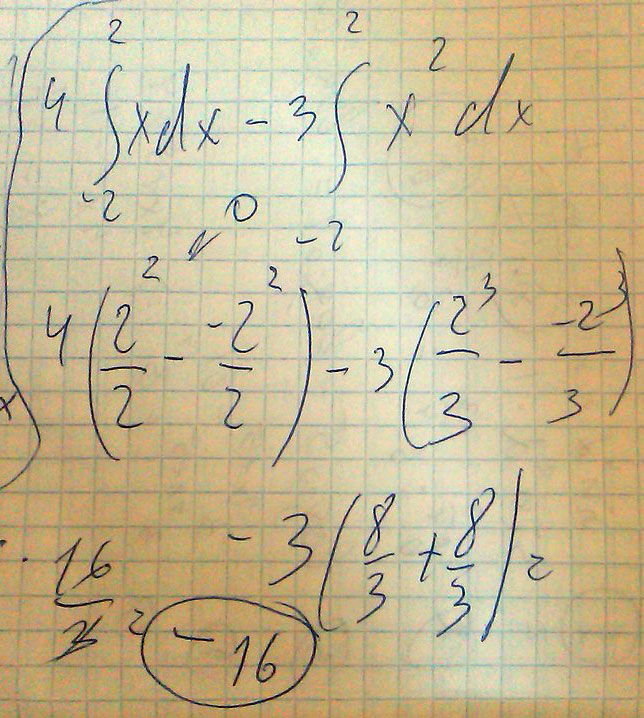

    int - x- x dx frac x - frac x - x -x - - - -...

  • Вычислите интеграл: \( \int\limits^ \frac{1}{3} _ {0} \, \frac{dx}{ (6x-1)^{4} } \)


    Решение: Отыет  0
    -

    Попробуем посчитать интеграл, "отключив мозг":
    $$ \displaystyle\int\limits^ {1/3} _ {0} \, \dfrac{dx}{ (6x-1)^{4} } =\dfrac16\int\limits_0^{1/3}(6x-1)^{-4}\,d(6x-1)=(?)=\frac16\left[\frac{(6x-1)^{-3}}{-3}\right]_0^{1/3}=\\=\frac16\left(-\frac13+\frac13\right)=0 $$
    Получаем странный результат - интеграл от положительной функции равен нулю. Непорядок.
    Ошибка скрывается в переходе, обозначенном (?). Надо было бы написать так:
    $$ \displaystyle\dfrac16\left(\int\limits_0^{1/6}+\int\limits_{1/6}^{1/3}\right)(6x-1)^{-4}\,d(6x-1) $$
    Расписывая каждый интеграл по отдельности, становится понятно, что интеграл расходится (связано это с "нехорошей точкой" 1/6).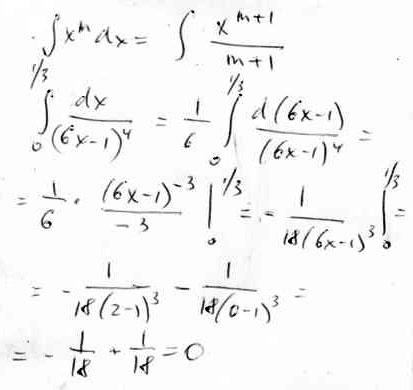

    Отыет  - Попробуем посчитать интеграл отключив мозг displaystyle int limits dfrac dx x- dfrac int limits x- - d x- frac left frac x- - - right frac left - frac frac right Пол...

  • Вычислить интеграл: \( \int\limits_0^2 2dx= \\ \int\limits_0^{\pi}(sinx)dx\\ \int\limits_2^e \frac{1}{x}dx=\\ \int\limits_{-1}^3(x^2+5x-4)dx= \\ \int\limits_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\frac{2}{cos^2x}dx =\)

    2. Определить и вычислить площадь плоских фигур и начертить график: 1) y=x; x=4; y=0
    2) y=x^2 +2; y=6
    3) y=sinx; y=3sinx; \(0\leq x\leq \pi \)


    Решение: №1

    1) Превоообразная = 2x

    Интеграл = 2*2-0 = 4

    2) первообразная = -cosx

    Интеграл = 1+1=2

    3) Превообразная 1/3 * X^3 +2,5x^2-4x

    Интеграл = 9+22,5-8+1/3-2,5-4=17 +1/3

    4) Первообразная 2 tg(x)

    Интеграл= 2+2=4

    №2

    1) S=0.5*4*4=8

    2) Площадь прямоугольника под у=6 S1=6*4=24

      Площадь под графиком Y=x^2+2 на промежутке от -2 до 2 S2=40/3

      Искомая площадь = 24 -40|3=10+2/3

    3) Превообразные: y=-cosx и y=-3cosx соответсвенно

    S=6-2=4

<< < 91011 12 13 > >>