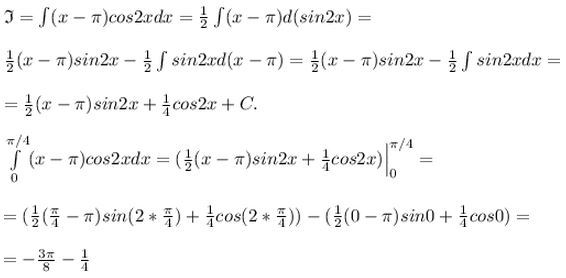интеграл »

вычислить интеграл - страница 14

  • Вычислить интеграл \( \int\limits^ \frac{ \pi }{6} _ \frac{ \pi }{12} { \frac{1}{ sin^{2}2x } } \, dx= \)


    Решение: Для начала нужно найти первообразную функции у=1/sin²2x, заметим, что производная функции у=ctgx выглядит так: у’=-1/sin²x, тогда первообразная для подынтегральной функции будет выглядеть следующим образом: F(x)=-1/2*ctg2x, тогда:
    $$ \int\limits^ \frac{ \pi }{6} _ \frac{ \pi }{12} { \frac{1}{ sin^{2}2x } } \\ dx=- \frac{1}{2}ctg2x |^{ \frac{ \pi }{6} } _{ \frac{ \pi }{12} }=(- \frac{1}{2}*ctg2* \frac{ \pi }{6})-(- \frac{1}{2}*ctg2* \frac{ \pi }{12})= \\= (- \frac{1}{2}ctg \frac{ \pi }{3})-(- \frac{1}{2}ctg \frac{ \pi }{6})=(- \frac{1}{2}* \frac{1}{ \sqrt{3} })-(- \frac{1}{2}* \sqrt{3})=\\= -\frac{1}{2 \sqrt{3}}+ \frac{ \sqrt{3} }{2}= \frac{2}{2 \sqrt{3} } \\ \frac{ \sqrt{3} }{3} $$

  • Вычислить интегралы
    ∫-8х²-4х-2 /-5хdx=
    ∫sin(-2x+5)dx=
    ∫x²lnxdx=


    Решение: $$ 1)\; \; \int \frac{-8x^2-4x-2}{-5x} dx=\int (\frac{8}{5}x+\frac{4}{5}+\frac{2}{5}\cdot \frac{1}{x})dx=\\\\=\frac{8}{5}\cdot \frac{x^2}{2}+\frac{4}{5}x+\frac{2}{5}\cdot lnx+C\\\\2)\; \; \int sin(-2x+5)dx=[\, t=-2x+5,\; dt=-2dx\, ]=\\\\=-\frac{1}{2}\int sint\, dt=-\frac{1}{2}\cdot (-cost)+C=\frac{1}{2}cos(-2x+5)+C\\\\3)\; \; \int x^2lnx\, dx=[\, u=lnx,\; du= \frac{dx}{x},\; dv=x^2\, dx,\; v=\frac{x^3}{3}\, ]= \\ =uv-\int v\, du= \frac{x^3}{3} lnx-\int \frac{x^2\, dx}{3} = \frac{x^3}{3}lnx- \frac{x^3}{9}+C $$

  • (37) Определенный интеграл. Интегрирование по частям \( \int \limits_{0}^{ \pi /4 }(x- \pi )cos2xdx \)


    Решение: $$ \mathfrak{I} =\int (x- \pi )cos2xdx= \frac{1}{2} \int (x- \pi )d(sin2x)=\\ \\ \frac{1}{2}(x- \pi )sin2x-\frac{1}{2} \int sin2xd(x- \pi )= \frac{1}{2}(x- \pi )sin2x-\frac{1}{2} \int sin2xdx= \\ \\ = \frac{1}{2}(x- \pi )sin2x+\frac{1}{4} cos2x+C. \\ \\ \int \limits_{0}^{ \pi /4 }(x- \pi )cos2xdx=(\frac{1}{2}(x- \pi )sin2x+\frac{1}{4} cos2x)\Bigr|_0^{\pi/4}= \\ =(\frac{1}{2}(\frac{ \pi }{4}- \pi )sin(2*\frac{ \pi }{4})+\frac{1}{4} cos(2*\frac{ \pi }{4}))-(\frac{1}{2}(0- \pi )sin0+\frac{1}{4} cos0)= \\ \\ =-\frac{ 3\pi }{8}-\frac{ 1 }{4} $$
    При вычислении площади фигуры используют абсолютную величину данного значения, т. е. число $$ |-\frac{ 3\pi }{8}-\frac{ 1 }{4}|=\frac{ 3\pi }{8}+\frac{ 1 }{4} $$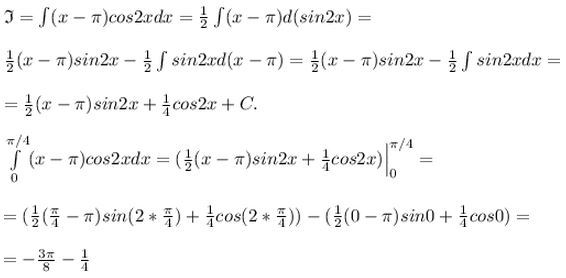

    mathfrak I int x- pi cos xdx frac int x- pi d sin x frac x- pi sin x- frac int sin xd x- pi frac x- pi sin x- frac int sin xdx frac x- pi sin x frac cos x C. int limits pi x-...

  • Вычислить интеграл, используя метод интегрирования по частям.
    ∫5x lnx dx. С объяснениями


    Решение: 1) Вынесем константу: $$ 5 \int{ x \cdot \ln{x}} \, dx $$
    2) Интегрируем по частям ($$ \int udv = uv - \int vdu $$)
    $$ u= \ln{x},\ du= \frac{dx}{x}; \ \ dv=x; \ v= \frac{x^{2}}{2} \\ 5 \cdot (\ln{x} \cdot \frac{x^{2}}{2} - \int \frac{dx}{x} \cdot \frac{x^{2}}{2} )=5 \cdot (\frac{x^{2}\cdot \ln{x} }{2} - \int \frac{x}{2}dx ) \\ =5 \cdot (\frac{x^{2}\cdot \ln{x} }{2} - \frac{1}{2}\int xdx )=5 \cdot (\frac{x^{2}\cdot \ln{x} }{2} - \frac{1}{2} \cdot \frac{x^{2}}{2} )+C= \\ 5x^{2} \cdot (\frac{\ln{x} }{2} - \frac{1}{4} )+C $$

  • Вычислить интеграл по частям \( \int\limits_e^4 xlnxdx \); Вычислить интегралы методом подстановки: \(\int\limits_4^5(4-x)^3dx \\ \int\limits_0^3 \sqrt[3]{3x-1}dx \\ \int\limits_0^1 e^{x^{2}}xdx \)


    Решение: 1
    u=lnx,dv=xdx
    du=dx/x,v=x²/2
    $$ \int\limits^4_e {xlnx} \, dx=uv-1/2 \int\limits {vdu} =1/2*x^2lnx-1/2*x^2/2|4-e= \\ 8ln4-4-e^2/2+e^2/4=8ln4-4-e^2/4 $$
    2
    $$ a) \int\limits^5_4 {(4-x)^3} \, dx =-(4-x)^4/4|5-4=-1/4+0=-1/4 \\ b) \int\limits^3_0 { \sqrt[3]{3x-1} } \, dx =1/4* \sqrt[3]{(3x-1)^4}|3-0=1/4*16-1/4*1=4- \ 0,25=3,75 $$
    в)u=x²,du=2xdx
    $$ \int\limits^1_0 {xe ^{x^2} } \, dx =1/2 \int\limits {e ^{u} } \, du =1/2*e^u=1/2*e ^{x^2} |1-0= \ 1/2*e-1/2 $$

<< < 121314 15 16 > >>