интеграл »
найти интеграл - страница 27
Интегралы. 1) \( \int\limits^3_2 { \frac{1-x^4}{1-x} } \, dx \)
2) \( \int\limits { \frac{cos2x}{cosx+sin \alpha } } \, dx \)
3) \( \int\limits { \frac{x^2+dx}{x^2+1} } \)
Решение: $$ 2) \int\limits\ \frac{cos^{2}x - sin^{2} x}{cosx-sinx} dx= \int\ (cosx+sinx) dx =sinx-cosx+C $$
1)$$ \int\limits^3_2 { \frac{1-x+x- x^{4} }{1-x} } \, dx = \int\limits^3_2 { \frac{(1-x)+(x- x^{4)} }{1-x} } \, dx = \int\limits^3_2 {1} \, dx + \int\limits^3_2 { \frac{x(1- x^{3}) }{1-x} } \, dx = \\ \int\limits^3_2{} \, dx+ \int\limits^3_2 { \frac{x(1- x)(1+x+x^{2}) }{1-x} } \, dx=\int\limits^3_2 {} \, dx+ \int\limits^3_2 {x(1+x+x^{2}) } \, dx= \\ \int\limits^3_2 {} \, dx+ \int\limits^3_2 {(x+ x^{2} + x^{3}) } \, dx =( x^{2} + \frac{ x^{3} }{3}+ \frac{ x^{4} }{4} )= $$=9+9+81/4-4-8/3-4=$$ 19 \frac{7}{12} $$Как найти интегралы 1. ʃcos^3(x) / sin^2(x) dx
2. ʃx*sin^2(x^2) dx
3. ʃe^x*cos^2(e^x) dx
Решение: $$ \int{x\cdot sin^2(x^2)}\, dx=\int{x\cdot \frac{1-cos(2x^2)}{2}}\, dx=\frac{1}{2}\int{x(1-cos(2x^2))}\, dx= \\ =\frac{1}{2}\int{(x-xcos(2x^2))}\, dx=\frac{1}{2}(\int{x}\, dx-\int{xcos(2x^2)}\, dx)=\frac{1}{2}\cdot\frac{x^2}{2}- \\ -\frac{1}{2}\cdot\frac{1}{4}\int{cos(2x^2)}\, d(2x^2)=\frac{1}{4}x^2-\frac{1}{8}sin(2x^2)+C, \\ \int{e^x\cdot cos^2(e^x)}\, dx=\int{e^x\cdot \frac{1+cos(2e^x)}{2}}\, dx= \\ =\frac{1}{2}\int{e^x(1+cos(2e^x))}\, dx=\frac{1}{2}\int{(e^x+e^xcos(2e^x))}\, dx= \\ \frac{1}{2}(\int{e^x}\, dx+\int{e^xcos(2e^x)}\, dx)=\frac{1}{2}e^x+\frac{1}{2}\cdot\frac{1}{2}\int{cos(2e^x)}\, d(2e^x)= \\ =\frac{1}{2}e^x+\frac{1}{4}sin(2e^x)+C. $$Найти интеграл sin^2x*sin3xdx
Решение: $$ sin ^{2}x= \frac{1-cos2x}{2} \\ \int {sin ^{2}x\cdot sin3x } \, dx = \int {\frac{1-cos2x}{2} \cdot sin3x } \, dx= \\ ={\frac{1}{2}\int sin3x } \, dx- {\frac{1}{2}\int cos2x\cdot sin3x } \, dx= \\ =\frac{1}{2\cdot3}(-cos3x)-{\frac{1}{2}\int {(\frac{1}{2}sin(3x+2x)+\frac{1}{2}sin(3x-2x))}}dx= \\ = \\ =\frac{1}{2\cdot3}(-cos3x)-{\frac{1}{4}}\int {sin5xdx-\frac{1}{4}}\int sinxdx = \\ =\frac{1}{2\cdot3}(-cos3x)- \frac{1}{4\cdot5}(-cos5x)\frac{1}{4}(-cosx)+C= \\ =-\frac{cos3x}{6}+ \frac{cos5x}{20}+\frac{cosx}{4}+C $$
Первообразную y=интеграл sinx(5x-1)
Решение: Раскрываете скобки, интеграл суммы равен сумме интегралов, интеграл xsinx решаете по частям и получаете ответ.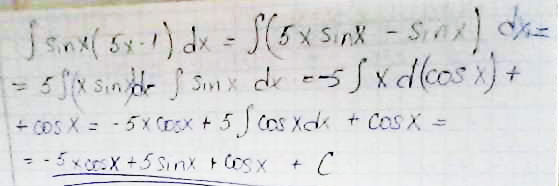
Найдите интегралы
1) знак интеграла от x^2+2x+3dx
2) знак интеграла sinx\( \sqrt{x} \)dx
3) знак интеграла arcsinxdx
4) знак интеграла \( 3^{x} dx \)
Решение: 1)
$$ \int{(x^2+2x+3)}dx=\int{x^2}dx+2\int{x}dx+3\int{}dx=\\ =\frac{1}{2+1}\cdot x^{2+1}+2\cdot\frac{1}{1+1}\cdot x^{1+1}+3\cdot\frac{1}{0+1}\cdot x^{0+1}+C=\\ =\frac{1}{3}x^3+\frac{2}{2}+\frac{3}{1}x^1+C=\frac{1}{3}x^3+x^2+3x+C;\\ $$
2)
$$ \int{\sin x\sqrt{x}}dx= $$
3)
$$ \int{\arcsin x}dx=\\ \left|\int{u}dv=u\cdot v-\int{v}du\right|\\ \left|u=\arcsin x;\ \ du=\frac{1}{\sqrt{1-x^2}}\right|\\ \left|dv=dx;\ \ \ \ \ \ \ \ v=x\ \ \ \ \ \ \ \ \right| \\ =x\cdot\arcsin x-\int{\frac{x}{\sqrt{1-x^2}}}dx=x\cdot\arcsin x+\frac{1}{2}\int{\frac{d(1-x^2)}{\sqrt{1-x^2}}}=\\ =x\cdot\arcsin x+\frac{1}{2}\int{(1-x^2)^{-\frac{1}{2}}}d{(1-x^2)}=\\ =x\cdot\arcsin x+\frac{1}{2}\cdot\frac{1}{-\frac{1}{2}+1}\cdot(1-x^2)^{-\frac{1}{2}+1}+C=\\ =x\cdot\arcsin x+\sqrt{1-x^2}+C $$
4)
$$ \int{3^x}dx=\frac{1}{\ln3}\cdot3^x+C;\\ $$