модуль »

как найти модуль

  • 1) Разложить на множители
    7140
    2) Найти НОК (наименьшое общее кратное) и НОД (наименьший общий делитель)
    924 И 396
    3) Записать в виде деления дроби
    8/21 (дробь)
    4) Записать в виде обыкновенной дроби
    0,(18) и 0,00(4)
    5) Примеры с модулями
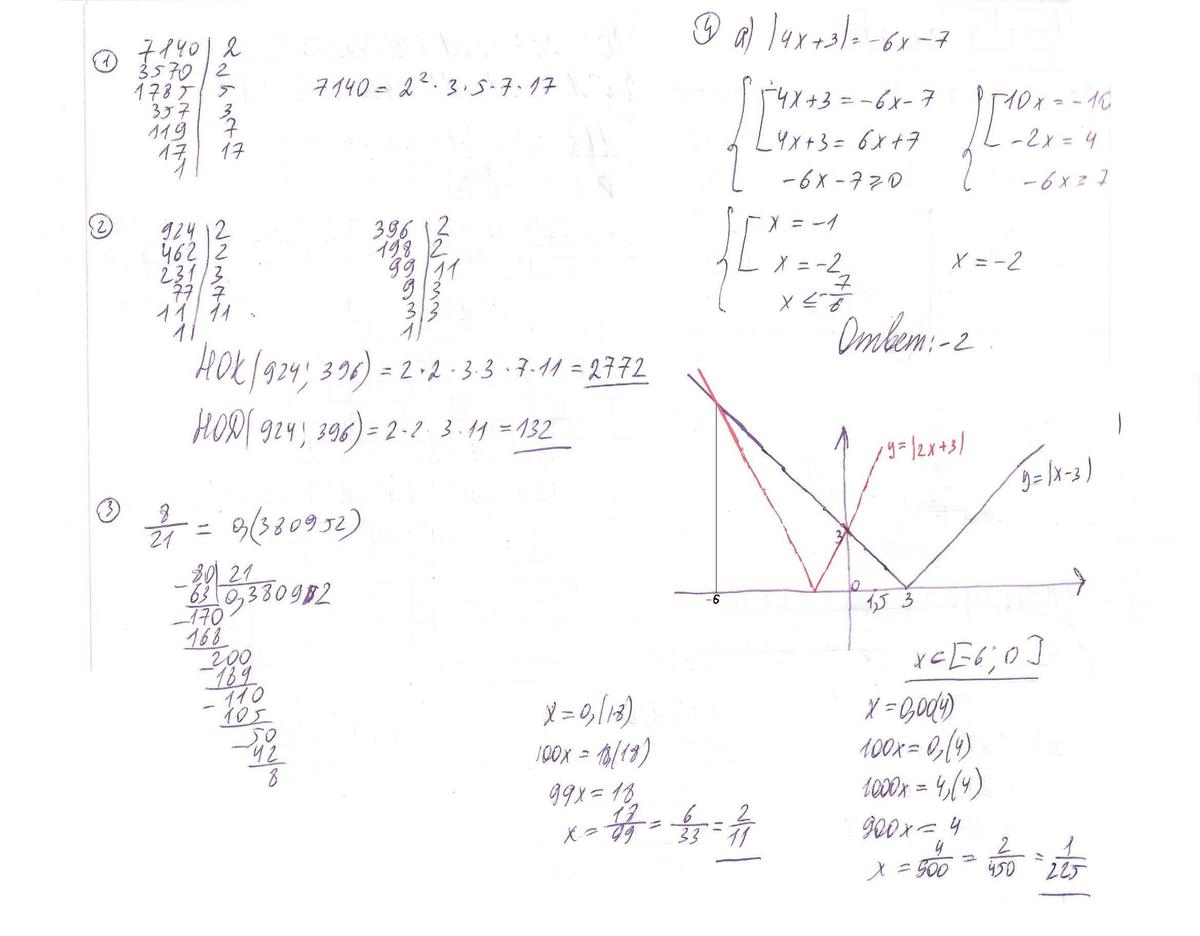
    а)|4x+3|=-6x-7
    б) |x-3|>(или равно)|2x+3|


    Решение: 1)  7140=10 *714=2*5*(2*357)=2^2*5*3*119
    2)  924=2^2*3*7*11
         396=2^2*3^2*11
    НОД(924,396)=2^2*3*11=132
    НОК(924,396)=2^2*3^2*5*7*11=13860
    3)8/21=0,38095238
    4)  x=0,(18)
    100x=18,(18)
    100x-x=99x=18,(18)-0,(18)=18   x=18/99
    b)  0,00(4)=x
    100x=0,(4)=y
    10y=4,(4)  10y-y=9y=4,(4)-0,(4)=4     y=4/9
    4/9=y=100x     x=4/900
     5)  |4x+3|=-6x-7   ->  4x+3=-6x-7  или  4x+3=6x+7
       10x=-10                2x=4
      x=-1 x=2  
    При проверке х=-1 не даёт верное равенство, остаётся только х=2
    6) |x-3|>= |2x+3|
     x-3=0, x=3
    2x+3=0, x=-1,5         - + + +
    Знаки модулей        -(-1,5)-(3)-  
                                    -  + + + + + +  
    В верхней строчке знаки (х-3), а в нижней - (2х+3)
    а) пусть х<-1,5, тогда неравенство перепишется так: -(х-3)>=-(2x+3)
    -x+3+2x+3>=0, x+6>=0, x>=-6    Так как получили иксы >=-6, а мы находимся в интервале х<-1,5, то -6<=x<-1,5
    б) пусть -1,5<=x<3, тогда -(x-3)>=2x+3,3x>=0, x<=0
    Окончательно имеем: -1,5<=x<=0
    в) х>=3, тогда х-3>=2х+3, x<=-6 - нет решения, т. к. должны иметь х>=3.
    Ответ: х Є [-6; -1,5) U[-1,5 ;0]= [-6;0] 
      
     

                  НОД НОК   x x x-x x -    x b    x x y y    y-y y -      y y x     x      x - x-    -    x - x-   или   x x    x -                  x   x - x   При проверке х -...

  • Решите урвнение.(5/7-дробь)(|x|Модуль)
    а) х-8=16-х
    б)-16х=4
    в)5х-9=14+3х
    г)5/7=10
    д)2(х-3)=-7(1-х)
    е)1-3(х-1)=2-7(1-х)
    ж)|x|=-2.


    Решение: А) х-8=16-х
    2x=24
    x=12
    б)-16х=4
    х=-4/16=-1/4 (дроби)
    в)5х-9=14+3х
    2х=23
    х=11,5=11 1/2
    г)5/7=10 Вы, видимо, забыли тут вставить х.
    д)2(х-3)=-7(1-х)
    2х-6=-7+7х
    -5х=-5
    х=1
    е)1-3(х-1)=2-7(1-х)
    1-3х+3=2-7+7х
    -3х-7х=2-7-1-3
    -10х=-9
    х=0,9=9/10
    ж)|x|=-2
    здесь нет решений, потому что модуль любого числа - число положительное. Даже отрицательного. (|-2|=2, к примеру)

  • -4; 0; 51; -15; -27; -62; 2.
    1. Назвать наибольшее число
    2. Число, имеющее наибольший модуль
    3. Наименьшее число
    4. Число, имеющее наименьший модуль
    5. Неотрицательные числа
    6. Как записать, что число – 51 – положительное число?
    7. Как записать, что число – 62-отрицательное ?
    8. Сравни два положительных числа
    9. Сравните два отрицательных числа
    10. Сравните два числа с разными знаками
    11. Запишите в тетради числа в порядке возрастания.
    12. Сравните каждое число с нулём.


    Решение: 1. 51
    2.62
    3.62
    4.0
    5.0,51,2
    6. Странный вопрос, ну вот вам вариации: 25+26; 50+1; 49+2 и тд. Конкретно из этих чисел, только 51.
    7. Принцип тот же: -30-32; -25-37 и тд. Конкретно из этих только -62.
    8.51>2
    9.4>-62
    10.15<2
    11.62,27,15,4,0,2,51
    12.4<0; 0=0; 51>0; -15<0; -27<0; -62<0; 2>0

    1. Наибольшее число 51;
    2. Число, имеющее наибольший модуль -62;
    3. Наименьшее число -62;
    4. Число, имеющее наименьший модуль 0;
    5. Неотрицательные числа 0, 2, 51;
    6. 51>0;
    7. – 62<0; 
    8. 0<2; 51>2;
    9.4>-15; -62<-27
    10. 2>0; -27<0; -27<2;
    11.62; -27; -15; -4; 0; 2; 51;
    12. – 62<0; -27<0; -15<0; -4<0; 0=0; 2>0; 51>0.

  • доказать что модуль х-у/1-ху меньше 1, если модуль х и модуль у меньше 1


    Решение: Нужно доказать, что $$ \frac {|x-y|}{|1-xy|}<1 $$

    так как левая и правая части неотрицательны, это неравенство равносильно следующему (поднесем обе части к квадрату, чтобы избавиться от модуля так как |a|^2=a^2)

    $$ \frac {(x-y)^2}{(1-xy)^2}<1; \frac {x^2-2xy+y^2}{1-2xy+x^2y^2}-1<0; \frac {x^2-2xy+y^2-(1-2xy+x^2y^2)}{(1-xy)^2}<0; \\ \frac {x^2-2xy+y^2-1+2xy-x^2y^2}{(1-xy)^2}<0; \frac {x^2+y^2-1-x^2y^2}{(1-xy)^2}<0; $$

    так как $$ (1-xy)^2>0 $$ (0 не может быть потому что знаменатель не может быть равным 0, а квадрат выражения всегда неотрицателен),

    то нужно доказать что справедливо неравенство

    $$ x^2+y^2-1-x^2y^2<0; -(1-x^2)+y^2(1-x^2)<0; (y^2-1)(1-x^2)<0; $$

    то справедливо так как (y^2-1<0; y^2<1; |y|<1) (|x|<1; x^2<1; 1-x^2>0)

    (один из множителей отрицателен, другой положителен - значит и произведение отрицательное).

    Таким образом цепочкой равносильных преобразований мы пришли к справедливому неравенству. Доказано

  • Модуль х - 2 меньше 3


    Решение: |x-2| <3
    Раскроем модуль:
    если х-2<0, то есть х <2 |  если х≥2
     -x + 2 <3  |  х-2<3
    -x <1  |  x < 5
    x> -1  |  x∈[2 ; 5)
    x∈(-1; 2)  |
       Общее решение - объединение двух промежутков:
       х∈ (-1 ; 5)

1 2 3 > >>