модуль »

как найти модуль - страница 3

  • Число целых решений неравенства (sqrt25-x^2)*|x-1|<=0 равно (корень из 25-х в квадрате умножить на модуль выражения х-1)
    1)2
    2)3
    3) 11
    4)5
    5)7


    Решение: $$ \sqrt{25-x^2}\cdot |x-1| \leq 0 $$
    Произведение <=0, если сомножители будут разных знаков, то есть
    $$ \left \{ {{\sqrt{25-x^2} \geq 0} \atop {|x-1| \leq 0}} \right. \; \; ili\; \; \left \{ {{\sqrt{25-x^2} \leq 0} \atop {|x-1| \geq 0}} \right. $$
    В первой системе модуль не может быть отрицательным, но может =0. Поэтому система сводится к такой 
    $$ \left \{ {{\sqrt{25-x^2} \geq 0} \atop {|x-1|=0}} \right. \; \left \{ {{25-x^2 \geq 0} \atop {x-1=0}} \right. \; \left \{ {{(x-5)(x+5) \leq 0} \atop {x=1}} \right. \; \left \{ {{-5 \leq x \leq 5} \atop {x=1}} \right. \; \to \; x=1 $$
    Во второй системе квадр. корень не может быть отрицательным, ео может =0. Поэтому система перепишется так:
    $$ \left \{ {{\sqrt{25-x^2}=0} \atop {|x-1| \geq 0}} \right. \; \left \{ {{x^2=25} \atop {x\in (-\infty,+\infty)}} \right. \; \left \{ {{x_1=-5,x_2=5} \atop {x\in (-\infty,+\infty)}} \right. \; \to \; x_1=-5,x_2=5 $$
    Всего будет три решения:  -5, 1, 5.

  • Напишите решение с формулами
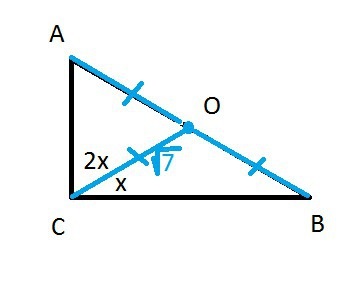
    Медиана проведенная к гипотенузе прямоугольного треугольника, делит прямой угол в отношении 1:2 и равна √7. Найти модуль разности квадратов катетов этого треугольника


    Решение: Медина делит гипотенузу пополам.
    Точка О- середина гипотенузы равноудалена от вершин А, В, С и  является центром описанной окружности.
    АВ- диаметр этой окружности, потому что прямой угол АСВ опирается на диаметр.
    АВ=2√7
    Пусть одна часть прямого угла С равна х, другая часть равна 2х.
    х+2х=90°
    х=30°
    2х=60°
    Медиана разбила прямоугольный треугольник на два равнобедренных треугольника с углами в 30° и 60°
    ∠АСО=∠ОАС=60°, сумма углов треугольника 180°, поэтому
    ∠АОС=60°.
    Треугольник АОС - равносторонний, АС=√7
    ВС²=АВ²-АС²=(2√7)²-(√7)²=28-7=21;
    ВС=√21.
    ВС²-АС²=(√21)²-(√7)²=21-7=14
    АС²-ВС²=(√7)²-(√21)²=-14
    Поэтому  вопрос о модуле разности,
    |ВС²-АС²|=|АС²-ВС²|=14.
    О т в е т. 14

    Медина делит гипотенузу пополам.Точка О- середина гипотенузы равноудалена от вершин А В С и  является центром описанной окружности. АВ- диаметр этой окружности потому что пря...

  • |3x² - x| = 8 + x - уравнение с модулем


    Решение: |3x² - x| = 8 + x
    т. к. модуль не может быть равен отрицательному числу, 
    следовательно, 8 + х ≥ 0, т. е. х ≥ -8
    нужно раскрыть модуль по определению:
    1) 3x² - x = 8 + x или 2) 3x² - x = -(8 + x)
      3x² - 2x - 8 =0 3x² + 8 =0
    D=4+12*8=4(1+24)=10² нет корней
    х₁ = (2-10)/6 = -4/3
    х₂ = (2+10)/6 = 2
    ПРОВЕРКА:
    |3(-4/3)² + (4/3)| = 8 - (4/3)
    |(16/3) + (4/3)| = 6 + (2/3)
    20/3 = 6 + (2/3) -верно))
    |3(2)² - 2| = 8 + 2
    |10| = 10 -верно))

  • модуль х-2 модуль більше рівне 10


    Решение: |x-2|≥10;

    x-2≥10; x≥12;

    x-2≤-10; x≤-8;

    Ответ: x∈(-∞;-8]U[12;+∞).

    |x-2|≥10

    x-2≥10 или x-2≥-10

    x≥10+2 x≥-10+2

    x≥12 x≥-8

    Числовой луч, две полные точки,8 и 12, штриховка в право! 

    x ∈ (-∞;-8| ∨ |12;+∞)

    ∨ - знак объединения если что!

  • Модуль (х - 7) = 2


    Решение: Х-7= 2 х=9
    х-7= -2 х=5
    Ответ: 9; 5

    Если $$ x \geq 7 $$, то выражение под модулем неотрицательное, поэтому модуль просто опускаем
    $$ |x-7|=2 \\ x-7=2 \\ x=9 $$
    Если $$ x \leq 7 $$, то выражение под модулем отрицательное, поэтому, когда опускаем знак модуля, меняем знаки в подмодульном выражении
    $$ |x-7|=2 \\ -(x-7)=2 \\ x=5 $$
    Ответ, х=9
    х=5

<< < 123 4 5 > >>