модуль »

как найти модуль - страница 10

  • Бросаются 2 игральных кубика, найти вероятность того, что модуль разности числа очков равен 2


    Решение: найдём количество благоприятны исходом(пар чисел):6 и 4, 5 и 3, 4 и 2, 3 и 1, и также в другом порядке т. е 1 и 3, 2 и 4, 3 и 5 4 и 6 т. е 8 благоприятных исходов всего исходов

    6*6=36 следовательно 8/36=2/9 вероятность того, что модуль разности числа очков равен 2

    При бросании кубика 2 раза число всех возможных исходов равно 36:

               11     12      13       14       15        16

               21     22      23       24       25        26

               31     32      33       34       35     36

               41     42      43       44       45        46

               51     52      53       54       55        56

               61     62      63       64       65        66

    модуль разности числа выпавших очков равен 2 только в 8 случаях: 

    1 3,    2 4,    3 5, 4 6,   3 1,  4 2,  5 3,  6 4

    Значит  вероятность того, что модуль разности числа выпавших очков равен 2, равна:

    8/36  =  2/9 = 0,2222. ≈  0,22

    Ответ:  0,22

             

  • 1) Дано; A(√2;1;2) B(√2;2;1) Найти: AB-вектор, AB-вектор в модуле
    2) Дано:A(-1/2;0;3/8), модуль AC=модулю BC, B(1/2;10;-5/8) Найти: C(x;y;z)
    3) Дано: модуль a(0;5;0) модуль b(0;-√3;1) Найти:cos(a"b)


    Решение: АВ вектор(0;1:-1) (из координат точки В нужно вычесть координаты точки А) Модуль вектора АВ= корень из 0^2+1^2++(-1)^2=корень из 2
    2) Модуль АС=корень из (х+1/2)^2+(y-0)^2+(z-3/8)^2
    Модуль из ВС=корень из (х-1/2)^2+(y-10)^2+(z+5/8)^2Получаем, что х^2+x+1/4=х^2-x+1/4
    x=0
    Y^2=y^2-20y+100
    20y=100
    y=5
    z^2-3/4z+9/64=z^2+5/4z+25/64
    -2z=25/64-9/64
    -2z=16/64
    z= -8/64= -1/8 C(0;5;-1/8)
    3) Cos (a"b)=-5√3/(√25*√4)=5√3/10=√3/2

  • |10 - 5х| = 1
    (Модуль 10 минус 5икс равен одному. Найти икс)


    Решение: $$ |10-5x|=1 \\ |-(5x-10)|=1 \\ |5x-10|=1 \\ 5x-10=\pm1 \\ 5x=10\pm1 \\ x=\frac{10\pm1}{5} \\ x=\frac{10+1}{5},or,x=\frac{10-1}{5} \\ x=\frac{11}{5},or,x=\frac{9}{5} $$
    Ответ: $$ \frac{11}{5};\frac{9}{5} $$

    I10-5xI=1
    Раскрываем модуль - получаем систему уравнений:
    10-5x=1 5x=9 x=1,8
    -(10-5x)=1 -10+5x=1 5x=11 x=2,2.

  • Найти площадь параллелограмма, построенного на векторах a - 2b и a + b, если модуль вектора а =sqrt 2, модуль вектора b = 4, угол (a, b)=45 градусам


    Решение: Обозначим
    $$ \vec c=\vec a-2\vec b \\ \\ \vec d=\vec a+\vec b $$
    Как известно, площадь параллелограмма равна длине вектора, который называется векторным произведением векторов с и d
    Выразим векторное произведение векторов с и d через данные векторы a и b 
     × - знак векторного произведения.
    $$ [\vec c \times \vec d]=[(\vec a-2\vec b)\times (\vec a+\vec b)]=\\=[\vec a \times \vec a]-2[\vec b\times \vec a]+[\vec a\times\vec b]+[\vec b\times \vec b]=0+2[\vec a\times \vec b]+[\vec a\times \vec b]=3[\vec a\times \vec b] $$
    Использованы дистрибутивные законы, скобки раскрыты по правилу умножения многочленов. Во втором слагаемом используем свойство антикоммутативности векторного произведения.
    Векторное произведение вектора а на вектор b численно равно площади параллелограмма построенного на векторах а и b:
    $$ S=|\vec a|\cdot |\vec b|\cdot sin \pi = \sqrt{2}\cdot 4 \cdot \frac{ \sqrt{2} }{2}=4 $$
    S параллелограмма построенного на векторах c и d  в три раза больше
    Ответ. 12  кв ед

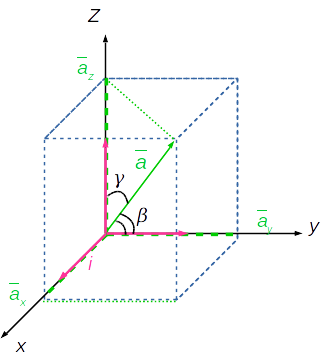
  • Найти вектор а образующий с тремя базисными векторами i j k равные острые углы при условии что модуль a = 2 корень 3


    Решение: Проекция вектора на соответствующую ось равна скалярному произведению
    вектора на единичный вектор
    $$ a_x=(a,i)=|a| \cdot |i| \cdot cos \alpha=|a|cos \alpha a_y=(a,j)=\\=|a| \cdot |j| \cdot cos \beta=|a|cos \beta a_z=(a,k)=|a| \cdot |k| \cdot cos \gamma=|a|cos \gamma $$  (1)
    Модули единичных векторов i,j,k равны естественно 1.
    α, β, γ - углы между вектором и осями (единичными векторами) 
    Кроме того должно выполняться равенство (своего рода теорема Пифагора для 3х мерного пространства)
    $$ |a|^2=a_x^2+a_y^2+a_z^2 $$  (2)
    Подставим в (2) выражения (1) и учтем, что углы равны:
    $$ |a|^2=|a|^2cos^2\alpha+|a|^2cos^2\beta+|a|^2cos^2\gamma=|a|^2\cdot 3cos^2\alpha 3cos^2\alpha=1 cos\alpha= \sqrt{ \frac{1}{3}} $$
    Ну и теперь можно найти компоненты вектора
    $$ a_x=a_y=a_z=2 \sqrt{3} \cdot \frac{1}{ \sqrt{3}} =2 $$

    Проекция вектора на соответствующую ось равна скалярному произведениювектора на единичный вектор a x a i a cdot i cdot cos alpha a cos alpha a y a j a cdot j cdot cos beta a...
<< < 8910 11 > >>