НОД и НОК »

как найти общее кратное чисел - страница 2

  • Найти наименьшее общее кратное чисел 15 и 18


    Решение: Что бы найти НОК (Наименьшее общее кратное) чисел, нужно:
    1. Разложить каждое число на множители.
    2. Выписать множители которые входят в каждое число.
    3. К списку множителей добавить числа которые входят в разложение одного из чисел.
    Разложим числа:
    $$ 15=3\cdot 5\\18=2\cdot 9=2\cdot 3\cdot3 $$

    Выписываем общие множители:
    $$ 3 $$

    Добавляем не общие множители:
    $$ 2\cdot 3\cdot 3\cdot 5=6\cdot 5=90 $$

    Ответ: НОК(15,18)=90

  • Надо найти наименьшее общее кратное чисел а018и45б)30и40в)210и350г)20,70и15


    Решение: общее кратное чисел а)18и45 б)30и40 в)210и350 г)20,70и15, если такое задание 

    а 180

    б 120

    в 1050

    г 420

    общее кратное чисел а)18и45 б)30и40 в)210и350 г)20,70и15

    НОК(18;45)=2*3*3*5=90

    НОК(30;40)=2*3*5*2*2=120

    НОК(210;350)=2*3*5*5*7=1050

    НОК(20,70,15)=2*2*5*7*3=420

  • Нужно найти наименьшее общее кратное чисел:
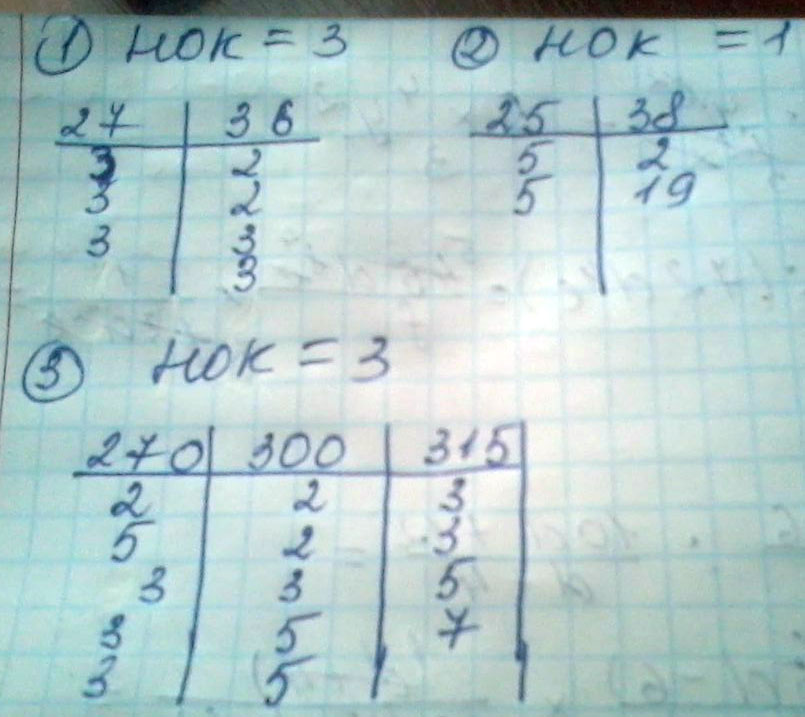
    1) 27 и 36
    2) 25 и 38
    3) 270, 300 и 315


    Решение: 27 = 3*3*3
    36 = 2*2*3*3
    НОК (27; 26) = 3*3*3*2*2 = 108
    25 = 5*5
    38 = 2*19
    НОК (25; 38) = 5*5*2*19 = 950
    270 = 2*3*3*3*5
    300 = 2*2*3*5*5
    315 = 3*3*5*7
    НОК (270; 300; 315) = 2*2*3*3*3*5*5*7 = 18900

    НОК НОК НОК ...

  • Даны разложения чисел га простые множители. найти наименьшее общее кратное a=2*3*7 и b=2*3*7


    Решение: 1) а = 2 * 2 * 3 * 7    b = 2 * 2 * 3 * 7      a = b 

    НОК (а; b) = 2 * 2 * 3 * 7 = 84 - наименьшее общее кратное

    2) с = 2 * 3 * 3 * 5       d = 2 * 2 * 5

    НОК (с; d) = 2 * 2 * 3 * 3 * 5 = 180 - наименьшее общее кратное

    3) е = 2 * 3 * 11       f = 2 * 2 * 2 * 3 * 11

    НОК (e; f) = 2 * 2 * 2 * 3 * 11 = 264 - наименьшее общее кратное

    4) h = 2 * 5 * 7         r = 5 * 5 * 7

    НОК (h; r) = 2 * 5 * 5 * 7 = 350 - наименьшее общее кратное

    5) m = 2 * 3 * 5 * 5         n = 2 * 2 * 2 * 2 * 3

    НОК (m; n) = 2 * 2 * 2 * 2 * 3 * 5 * 5 = 1200 - наименьшее общее кратное

    6) х = 2 * 5 * 11          у = 5 * 5 * 11

    НОК (х; у) = 2 * 5 * 5 * 11 = 550 - наименьшее общее кратное

    Чтобы найти НОК (а; b), нужно разложить данные числа на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.

  • Найти наименьшее общее кратное чисел удобным способом: 5 и 15


    Решение: 5 разложим. 5 ; 15 разложим 3*5. итак: 3 будет = 3. правило: чтобы найти НОК надо: 1) разложить их на простые множители,2) выписать множители, входящие в разложение одного из чисел,3) добавить к ним недостающие множители из разложений остальных чисел 4) найти произведение получившихся множителей!

<< < 12 3 4 > >>