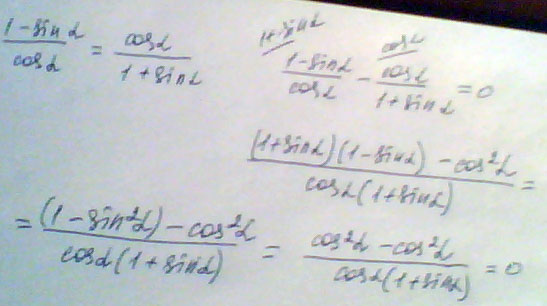докажите тождество - страница 2
Докажите тождество :
sin a / 1+ cos a + 1+cos a / sin a = 2 / sin a
решите уравнение :
sin в квадрате x - 6 sin x = 0
Решение: Приводим левую часть тождества к общему знаменателю:(sin^2a+(1+cosa)^2)/(1+cosa)sina=2(1+cosa)/(1+cosa)sina=2/sina что и т. д.
sinx(sinx-6)=0
sinx=6 решения нет
sinx=0
x=(пи)n, n принадлежит классу целых чисел
Приводим левую часть тождества к общему знаменателю:
(sin^2a+(1+cosa)^2)/(1+cosa)sina=2(1+cosa)/(1+cosa)sina=2/sina что и т. д.
sinx(sinx-6)=0
sinx=6 решения нет
sinx=0
x=(пи)n, n принадлежит классу целых чисел.
Докажите тождество:
\( sin x+cos x+ \sqrt{2}=2\sqrt{2}cos^2(\frac{x}{2}-\frac{\pi}{8}) \)
Решение: Воспользуемся 2 тригонометрическими формулами:1. $$ cos^2x=\frac{1+cos2x}{2} $$
2. $$ cos(x-y)=cosx\cdot cosy+sinx \cdot siny $$
Теперь воспользуемся первой формулой преобразуем левую часть выражения, получим:
$$ 2\sqrt{2}cos^2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$
Воспользуемся формулой 2. И упростим cos:
$$ \sqrt{2}(1+cos(x-\frac{\pi}{4}))= \\ =\sqrt{2}(1+cosx\cdot cos(\frac{\pi}{4})+sinx \cdot sin(\frac{\pi}{4}))= \\ =\sqrt{2}(1+cosx\cdot \frac{\sqrt{2}}{2}+sinx \cdot \frac{\sqrt{2}}{2}) \\ =\sqrt{2}+cosx+sinx $$
Получаем что левая часть равна правой части:
$$ sinx+cosx+\sqrt{2}=\sqrt{2}+cosx+sinx $$
Что и требовалось доказать
Докажите тождество: sin(45-альфа) / cos(45-альфа)=1
Тема: синус и косинус разности
Решение: sin(45-альфа) / cos(45-альфа)=1
sin45cosA-cos45sinA/cosAcos45+sin45sinA=cosA-sinA/cosA+sinA не равно 1
cos(45+фльфа)=cos45cosA-sin45cosA при таком знаменателе =1
Докажите тождество:
1) 1-sin t / cos t=cos t / 1+sin t
2)sin t / 1-cos t=1+ cos t / sin t
Решение: Умножаем крест на крест
cos^2t=(1-sint)(1+sint)
cos^2t=1-sin^2t
cos^2t+sin^2t=1
1=1
2)(1+cost)(1-cost)=sin^2t
1-cos^t=sin^2t
1=sin^2t+cos^2t
1=1. В данном случае метод доказательства разность между левой и правой частями =0
второй номер доказывается аналогично
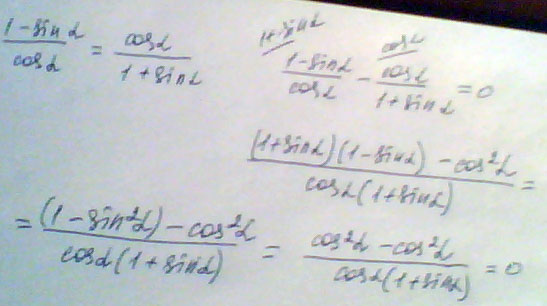
докажите тождество sin^4a+sin^2a cos^2a=1-cos^2a
Решение: используя основное тригонометриеское тождество$$ sin^4 a+sin^2 a cos^2 a=sin^2 a(sin^2+cos^2 a)=sin^2 a*1=sin^2 a=1-cos^2 a $$
Доказано
в левой части выносим за скобки sin²a:
sin²a(sin²a+cos²a)=1-cos²a
в правой части применяем основное тригонометрическое тождество:
sin²a(sin²a+cos²a)=sin²a
sin²a сокращается
sin²a+cos²a=1, а это основное тригонометрическое тождество. ч. т. д