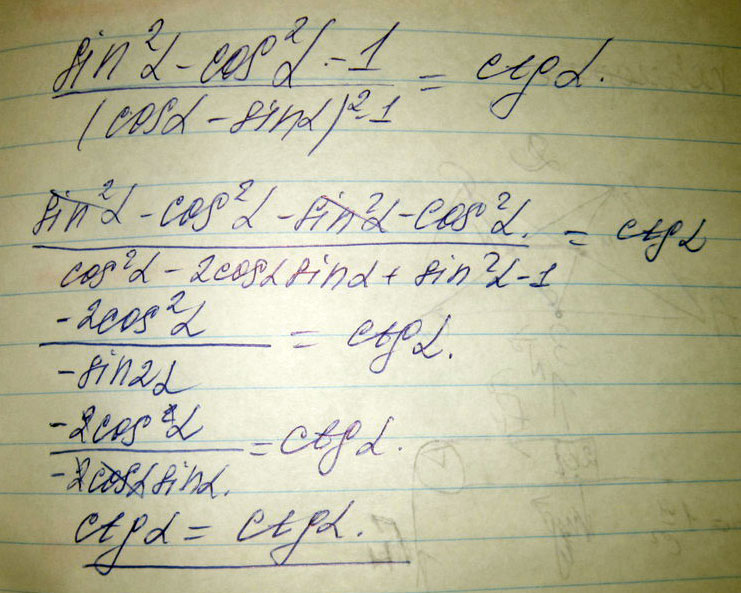тождество »

докажите тождество - страница 3

  • Докажите тождество:
    cos^4t-sin^4t=cos2t


    Решение: Раскладываем левую часть как разность квадратов:
    $$ cos^4t-sin^4t=(cos^2t)^2-(sin^2t)^2=(cos^2t-sin^2t)*(cos^2t+sin^2t) $$
    Второй множитель  по основному тригонометрическому тождеству всегда равен 1, первый равен косинусу  двойного угла по соответствующей формуле. Значит, цепочку равенств можно продолжить: $$ (cos^2t-sin^2t)*(cos^2t+sin^2t)=cos(2t)*1=cos(2t) $$, т. е. левая часть равна правой при любом t. Тождество доказано.

  • Докажите тождество
    \( \frac{sin^{2} \alpha - cos^{2} \alpha - 1 }{(cos \alpha - sin \alpha)^{2} - 1 } = ctg ( \pi + \alpha ) \)


    Решение: $$ \frac{sin^{2} \alpha - cos^{2} \alpha - 1 }{(cos \alpha - sin \alpha)^{2} - 1 } =\\= ctg ( \pi + \alpha ) \\ \\ \frac{sin^{2} \alpha - cos^{2} \alpha - 1 }{(cos \alpha - sin \alpha)^{2} - 1 }=\\ =\frac{sin^{2} \alpha - cos^{2} \alpha - sin^2\alpha-cos^2\alpha }{cos^2 \alpha -2sin\alpha cos\alpha+ sin^2 \alpha - 1 }=\\=\frac{-2cos^2\alpha}{1-2sin\alpha cos\alpha-1}=\frac{-2cos^2\alpha}{-2sin\alpha cos\alpha}= \\ \\ =\frac{cos\alpha}{sin\alpha}=ctg\alpha=ctg(\pi+\alpha) $$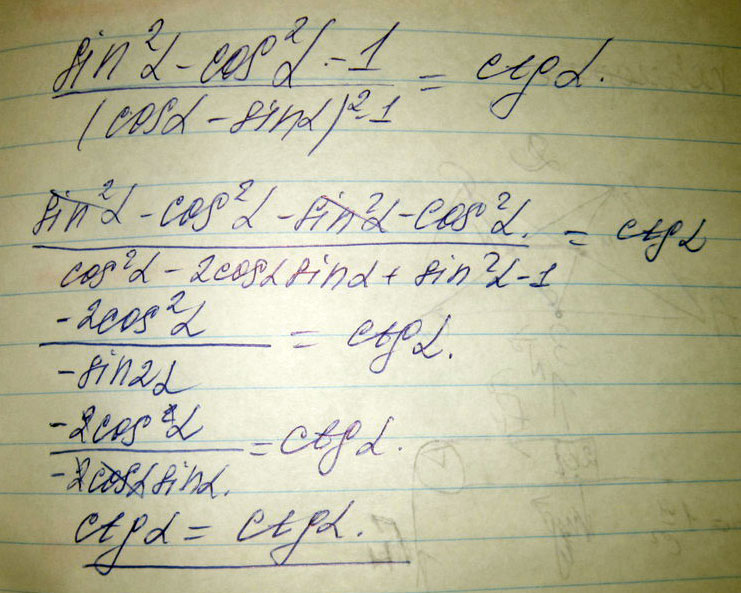

    frac sin alpha - cos alpha - cos alpha - sin alpha - ctg pi alpha frac sin alpha - cos alpha - cos alpha - sin alpha - frac sin alpha - cos alpha - sin alpha-cos alpha cos al...

  • Докажите тождество.sin^4a +sin^2*cos^2a cos^2a=1


    Решение: По действиям:

    Выносим sin^2a за скобки: 

    sin^4a + sin^2a*cos^2a + cos^2a = sin^2a (sin^2a+cos^2a) + cos^2a;

    Вспоминаем, что в скобках единица по основному тригонометрическому тождеству: 

    sin^2a(sin^2a+cos^2a) + cos^2a = sin^2a+cos^2a;

    и опять в скобках единица =>

    sin^2a+cos^2a=1; 1=1 тождество верно. 

  • 1) сравните значения выражения:
    cos 25п/13 tg 11п/10 и sin(-330 градусов)ctg 100 градусов
    2) докажите тождество:
    ((cos^4A-sin^4A)/(1-sinA)(1+sinA))+2tg^2A=1/cos^2A
    3) упростите выражение:
    ctg^6B-((cos^2B-ctg^2B)/sin^2B-tg^2B))
    4) докажите тождество:
    sinA-cosB/sinB+cosA=sinB-cosA/sinA+cosB


    Решение:           Решение :
    1) сравните значения выражения:
    cos 25п/13 tg 11п/10 и sin(-330 градусов)ctg 100 градусов
    cos25П/13=cos(П/13)>0
    tg11П/10=tgП/10=tg18>0
    ctg100=ctg(90+10)=-tg10<0
    sin(-330)=sin(-330+360)=sin30>0
    cos 25п/13 tg 11п/10>sin(-330 градусов)ctg 100 градусо
    2) докажите тождество:
    ((cos^4A-sin^4A)/(1-sinA)(1+sinA))+2tg^2A=1/cos^2A
    (cos^2a-sin^2a)/(1-sin^2a)+2tg^2a=(cos^2a-sin^2a)/cos^2a+2tg^2a=1+tg^2a=1/cos^2a
    3) упростите выражение:
    ctg^6B-((cos^2B-ctg^2B)/sin^2B-tg^2B))
    ctg^6b-cos^4b(sin^2b-1)/sin^4b(cos^2b-1)=ctg^6b+ctg^6b=2ctg^6b
    4) докажите тождество:
    sinA-cosB/sinB+cosA=sinB-cosA/sinA+cosB
    (sina-cosb)(sina+cosb)-(sinb-cosa)(sinb+cosa)=sin^2a-cos^2b-sin^2b+cos^2a=0.

  • Докажите тождество

    cos^2 a-sin^2 a\\cos a-sin a -tg a *cos a =cos a


    Решение: cos^2 a-sin^2 a\\cos a-sin a -tg a *cos a =cos a

    (cos a-sin a)(cos a+sin a)\(cos a-sin a) -(sin a/cos a) *cos a =cos a

    cos a+sin a-sin a =cos a
    cos a=cos a

    Cos^2a-sin^2a/cos a - sin a - tg a* cos a=

    = cos a - sin a/-tg a* cos a(сократили кос и син внизу, убрав квадраты наверху)=

    =- sin a/- tg a(сократили косинусы)=cos a(по определению tg a=sin a/cos a, => cos a=sin a/ tg a). Доказано.

<< < 123 4 5 > >>