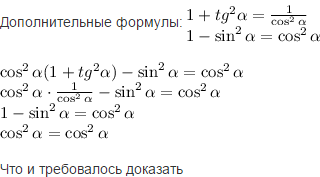докажите тождество - страница 5
1) ДОКАЖИТЕ ТОЖДЕСТВО: cos(a-90)+sin(a-180)+tg^2(180-a)+ctg^2(a-180)=tg^2(a)+ctg^2(a)
2)sin(t)=5/13 pi>t>pi/2, найти cos(t),tg^2(t),sin^2(t)
Решение: Cos(α-90)=cos(-(90-α))=cos(90-α)=sinα
sin(α-180)=sin(-(180-α))=-sin(180-α)=-sinα
tg²(180-α)=(tg(180-α))²=(-tgα)²=tg²α
ctg²(α-180)=(ctg(-(180-α)))²=(-ctg(180-α))²=(ctgα)²=ctg²α
cos(α-90)+sin(α-180)+tg²(180-α)+ctg²(α-180)=sinα-sinα+tg²α+ctg²α=tg²α+ctg²α
tg²α+ctgα=tg²α+ctg²α
2. sin²t=(5/13)², sin²t=25/169
sin²t+cos²t=1
cos²t=1-(5/13)², cos²t=144/169
cost=+-12/13, π/2<t<π, ⇒cost<0
cost=-12/13
tg²t=sin²t/cos²t, tg²t=(25/169)/(144/169).
tg²t=25/144$$ 1)cos(a-90)+sin(a-180)+tg ^{2} (180-a)+ctg ^{2} (a-180)= \\ =tg ^{2} a+ctg ^{2} a \\ \\ cos(a-90)+sin(a-180)+tg ^{2} (180-a)+ctg ^{2} (a-180)= \\ =cos(90-a)-sin(180-a)+tg^{2} a-ctg ^{2} (180-a)= \\ =sina-sina+tg ^{2} a+ctg ^{2} a=tg ^{2} a+ctg ^{2} a \\ 2)sint= \frac{5}{13} ;t\in ( \frac{ \pi }{2} ; \pi ) \tot\in II \\ \\ cost=- \sqrt{1-sin ^{2} t} =- \sqrt{1- (\frac{5}{13} ) ^{2} } =- \sqrt{1- \frac{25}{169} } =- \sqrt{ \frac{169-25}{169} } = \\ \\ =- \sqrt{ \frac{144}{169} } =- \frac{12}{13} \\ \\ sin ^{2}t = \frac{25}{169} \\ \\ cos ^{2} t= \frac{144}{169} \\ \\ tg ^{2} t= \frac{sin ^{2} t}{cos^{2} t} = \frac{25}{169} : \frac{144}{169} = \frac{25*169}{169*144} = \frac{25}{144} $$
Cos^2a(1+tg^2a)-sin^2a=cos^2a докажите тождество
Решение: Дополнительные формулы: $$ 1+tg^2 \alpha = \frac{1}{\cos^2 \alpha } \\ 1-\sin^2 \alpha =\cos^2 \alpha \\ \cos^2 \alpha (1+tg^2 \alpha )-\sin^2 \alpha =\cos^2 \alpha \\ \cos^2 \alpha \cdot \frac{1}{\cos^2 \alpha } -\sin^2 \alpha =\cos^2 \alpha \\ 1-\sin^2 \alpha =\cos^2 \alpha \\ \cos^2 \alpha =\cos^2 \alpha $$
Что и требовалось доказать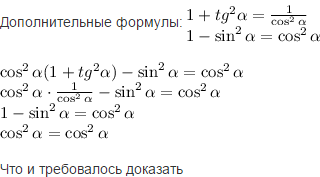
Упрастите выражение (sin2a-cosa)/(2sina-1)
докажите тождество cos(a-b)+sin(-a)*sin(-b)=cosa cosb
Решение: $$ 1) \frac{sin2 \alpha -cos \alpha }{2sin \alpha -1}= \frac{2sin \alpha\cdot cos \alpha -cos \alpha }{2sin \alpha -1}= \frac{cos \alpha (2sin \alpha-1) }{2sin \alpha -1}=cos \alpha $$
2) применяем формулу cos (α+β)=cosβcosβ-sinαsinβ,
так как функция sin х - нечетная, то sin(-α)=-sinα, sin (-β)=-sinβ
$$ cos( \alpha + \beta )+sin(- \alpha )\cdot sin(- \beta )= cos \alpha \cdot cos \beta \\ cos \alpha\cdot cos \beta -sin \alpha \cdot sin \beta +sin \alpha \cdot sin \beta =cos \alpha \cdot cos \beta \\ cos \alpha \cdot cos \beta =cos \alpha \cdot cos \beta $$
равенство cos(α-β)+sinα·sinβ=cosαcosβ+sinα·sinβ+sinα·sinβ≠cosα·cosβ1. Докажите тождество: cos^2t/1-sint (дробь) - sin^2t - cos^2t= sint
2. Известно, что tg t= 7/24 (дробь), пи < t < 3пи/2 (дробь)
Вычислить sint, cost, ctg t.
Решение: 1) Итак, t лежит во второй четверти. Из основного тригонометрического тождества sin^2a+cos^2a=1 => cos^2a=1-sin^2a => cosa=(+/-) корень из(1-sin^2a). Теперь к нашему примеру. Найдем косинус. Так как t лежит во второй четверти, где косинус отрицательный, перед корнем ставим знак минус: cost=-корень из(1-(8/17)^2)=-корень из(1-(64/289))=-корень из(225/289)=-15/17.
Далее tgt=sint/cost=(8/17)/(-15/17)=-8/15
ctg=1/tgt=cost/sint=-15/8
2) ctgt=1/tgt=-35/12
t лежит во второй и третьей четверти.
Имеем формулу: 1+tg^2a=1/cos^2a => cos^2a=1/(1+tg^2a). Переходим к нашему примеру.
cos^2t=1/(1+tg^2t)=1/(1+(-12/35)^2)=1/(1+144/1225)=1/(1369/1225)=1225/1369
Т. е. получили, что cos^2t=1225/1369. Тогда cost=-корень из (1225/1369)=-35/37
Перед корнем ставится знак минуса, потому что косинус во второй и третьей четверти отрецательный. Найдем синус из формулы tgt=sint/cost -12/35=sint/(-35/37) => sint=(-12/35)*(-35/37)=12/371. Докажите что верно равенство sin20+sin40-cos10=0
2. упростите выражение: sin3a-sin a* cos2a
_______________
sin3a+sin a
3. докажите тождество : sin4a +2cos3a-sin2a
________________ =ctg3a
cos4a -2sin3a-cos2a
Решение: sin20+sin40-cos10=0Сложим синусы по формулам суммы:
2sin30*cos10-cos10=0
Вынесем общий множитель:
cos10(2sin30-1)=0
Произведение равно 0, когда хотя бы один из множителей равен 0, в данном случае
(2sin30-1)=(2*1/2-1)=0
2.sin3a-sina*cos2a
По формулам произведения умножим синус на косинус:
sin3a-1/2 (sin(-a)+sin3a)=sin3a+1/2 sina - 1/2 sin3a=1/2(sin3a+sina)
По формулам суммы сложим синусы:
1/2(sin3a+sina)=1/2*2sin2a*cosa = sin2a*cosa=2sina*cosa*cosa = 2sina*cos^2 a
3.$$ \frac{sin4a+2cos3a-sin2a}{cos4a-2sin3a-cos2a}=-ctg3a $$
Т. к. в правой части ничего изменить нельзя, то будем работать только с левой части уравнения, пытаюсь представить ее в виде -ctg3a.
В числители вычтем синусы, в знаменателе - косинусы.
$$ \frac{sin4a+2cos3a-sin2a}{cos4a-2sin3a-cos2a}=\frac{2sina*cos3a+2cos3a}{-2sin3a*sina-2sin3a} $$
Вынесем в числителе и знаменателе общий множитель:
$$ \frac{2cos3a(sina+1)}{-2sin3a(sina+1)} $$
Сокращаем и получаем -cos3a/sin3a=-ctg3a