тождество »

докажите тождество - страница 7

  • Докажите тождество
    \( \frac{cos \alpha }{1-sin \alpha } = \frac{1+sin \alpha}{cos \alpha } \)


    Решение: Домножаем обе части равенства на произведение знаменателей:
    $$ cos \alpha \cdot cos\alpha=(1+sin\alpha)\cdot(1-sin\alpha) \\\\ cos^2\alpha=1-sin^2\alpha \\\\ cos^2\alpha+sin^2\alpha=1 $$
    Получили основное тригонометрическое тождество. Что и требовалось доказать.
    PS: надо бы еще указать область определения: $$ \alpha eq \frac{ \pi }{2}+\pi k \; (k \in Z) $$

  • Sin^4a+cos^4a+2sin^2a*cos^2a=1
    докажите тождество


    Решение: В левой части "сворачиваем" квадрат двучлена=(sin^2(x)+cos^2(x))^2=в скобках 1, т. е. 1^2=1. все. доказано.

    $$ sin^4 \alpha +cos^4 \alpha +2sin^2 \alpha *cos^2 \alpha =1 \\ (sin^2 \alpha)^2 +(cos^2 \alpha)^2 +2sin^2 \alpha *cos^2 \alpha =1 \\ (sin^2 \alpha+cos^2 \alpha)^2 =1 \\ 1^2=1 $$ 
    ч. т. д.
    P.S. $$ sin^2 \alpha+cos^2 \alpha =1 $$
      $$ a^2+b^2+2ab=(a+b)^2 $$

  • Докажите тождество

    а) cos x cos2x cos4x = sinx/ 8 sin x

    б) sin x cos 2x = sin 4x/ 4 cos x

    в) sin x cos 2x cos 4x = sin 8x/ 8 cos x


    Решение: 1) Множим на син что делиться на син(имеем право домножить потому что син\син =1), умножим числитель и знаменатель на 2 и применим формулу синуса двойного аргумента (2sinxcosx=2sinx)
    Выходит 2 sinx cosx cos 2x cos4x

    - = 2sin2xcos2xcos4x

    2sinx -= 2sin4x cos4x

     4sinx - = sin8x 

     8sinx

    б) умножаем и делим на 4кос кс, сначала на 2 кос кс потом потом просто на 2
    2cosxsinx cos2x
    - =sin2xcos2x 

    2cosx -=*2

     2cosx - = 2sin2x cos2x

    2 - = sin4x

    4cosx -

    4cosx

    в) sinxcos2xcos4x=sin8x\8cosx

    множим и делим на 2 cosx, потом 2 раза множим и делим на 2

    2sinx cosx cos2x cos4x
    -= 2sin2x cos2x cos4x

    2cosx - = 2sin4x cos4x
     

    4cosx - = sin8x
      

    8cosx

  • Докажите тождество: cos(60+x)cosx+sin(60+x)sinx=0.5


    Решение: $$ \cos(60а+x)\cos x+\sin(60а+x)\sin x=\\=\cos(60а+x-x)=\cos60а= \frac{1}{2} $$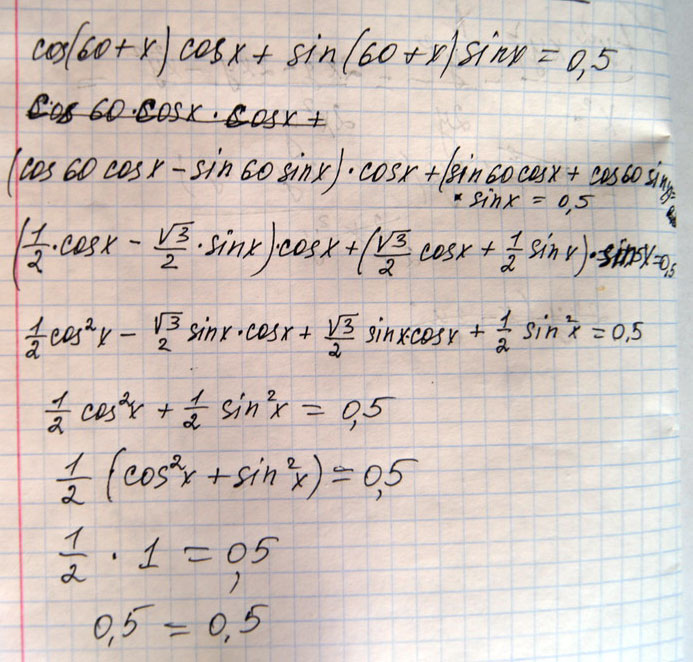

    cos а x cos x sin а x sin x cos а x-x cos а frac...

  • Докажите тождество
    1) 1+2sinacosa / (sina+cosa)^2 =1
    2) sin^2a-cos^2a+1 / sin^2a=2
    3) (2-sina)(2+sina)+(2-cosa)(2+cosa)=7


    Решение: $$ 3) (2-sin \alpha)(2+sin \alpha)+ (2-cos \alpha)(2+cos \alpha)=7 \\ 4-sin^{2} \alpha +4-cos^{2} \alpha =7 \\ 8-(sin^{2} \alpha +cos^{2} \alpha )=7 \\ 8-1=7 \\ 7=7 \ 1) \frac{1+2sin \alpha cos \alpha }{(sin \alpha +cos \alpha )^{2}}=1 \\ \frac{1+2sin \alpha cos \alpha }{(sin^{2} \alpha +2sin \alpha cos \alpha + cos^{2} \alpha )}=1 \\ \frac{1+2sin \alpha cos \alpha }{(1 +2sin \alpha cos \alpha)}=1 \\ 1=1 \\ 2) \frac{sin^{2} \alpha -cos^{2} \alpha +1}{sin^{2} \alpha } =2 \\ \frac{sin^{2} \alpha -cos^{2} \alpha +sin^{2} \alpha +cos^{2} \alpha}{sin^{2} \alpha } =2 \\ \frac{2sin^{2} \alpha }{sin^{2} \alpha } =2 \\ 2=2 \\ $$

    1) 1+2sinacosa / (sina+cosa)^2 =(sin²a+cos²a+2sinacosa)/(sin²a+2sinacosa+cos²a)=1
    2) sin^2a-cos^2a+1 / sin^2a=(sin²a-cos²a+sin²a+cos²a)/sin²a=2sin²a/sin²a=2
    3) (2-sina)(2+sina)+(2-cosa)(2+cosa)=4-sin²a+4-cos²a=8-(sin²a+cos²a)=8-1=7

<< < 567 8 9 > >>