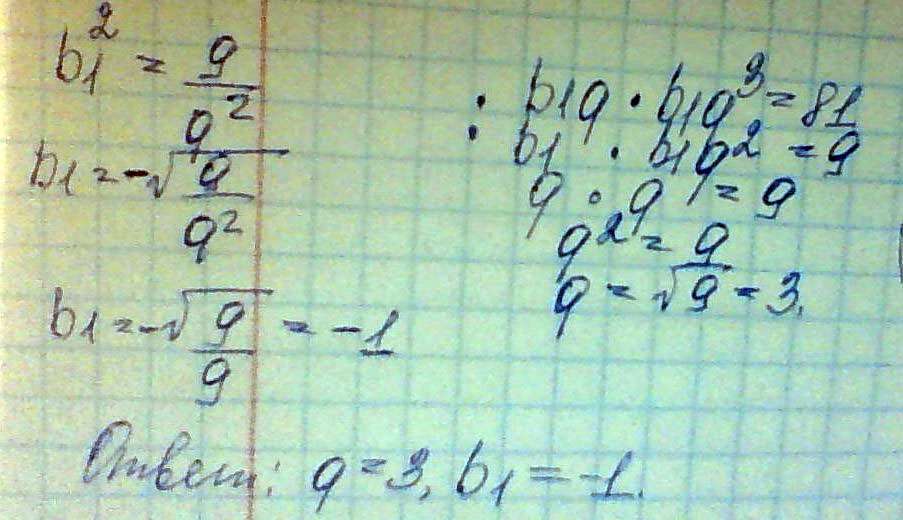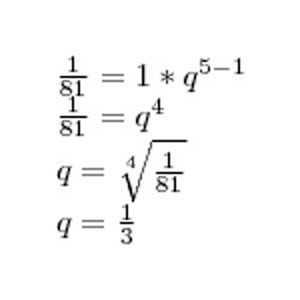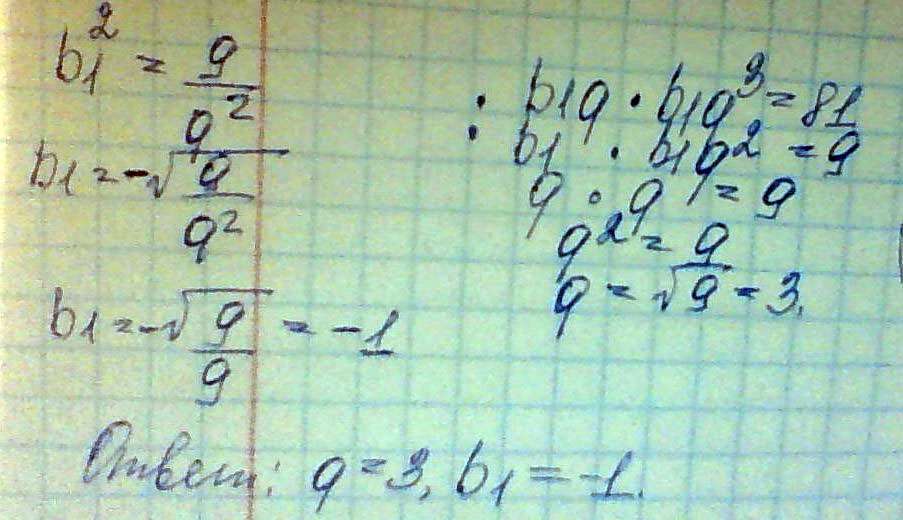второй член геометрической прогрессии
1. Сократить дробь. (9а^2-4b^2) / (2b+3a)^2 знаки ^-возведение в степень /-деление(дробь)
2.Решить систему уравнений. первое: 25х+2у=30 второе 5х-2у=-6 3.Найдите знаменатель геометрической прогрессии, если 30 ее член=31,а 31=32 4.Упростить: корень из 3,5 умноженный на корень из 2,1 делится как черта дроби на корень из 0,15
Решение: 1)(9a^2-4b^2)/(2b+3a)^2=(3a-2b)(3a+2b)/(2b+3a)^2 = (3a-2b)(2b+3a)2)
{25x+2y=50
{5x-2y=-6
{2y=50-25x
{5x-50+25x=-6
{30x=44
{x=22/15{y=20/3
3) b30=31
b31=32
q=b31/b30=32/31
4) V3.5*V2.1/V0.15=V49=7
Другое решение...

Чему равен знаменатель геометрической прогрессии, если ее второй член равен 1, а шестой 1/81?
Решение: Дано: b2=1, b6=1/81. Так как q=const, воспользуемся формулой:
Для этого представим новую последовательность, где b1=1, b5=1/81. Тогда получим (см. рисунок)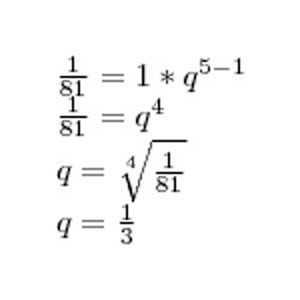
1)найти сумму первых четырех членов геометрической прогрессии 2,8
2)найти знаменатель геометрической прогрессии, если первый ее член равен 4, а третий равен 108
3) сумма второго и пятого членов геометрической прогрессии равна 84, а сумма третьего и шестого равна 252. найти сумму первых пяти членов этой прогрессии.
Решение: 1)найти сумму первых четырех членов геометрической прогрессии 2,8b1=2
b2=-8
n=4
q=b2/b1=-8/2=-4
сумма 4 первых членов геом. прог.
подставим известные значения:
S4=(2*((-4)*(-4)*(-4)*(-4)-1)):(-4-1)=(2*(256-1)):(-5)=-2*255/5=-2*51=-102
ответ: -102
2) я решила, можете посмотреть в "добавлено" =)
3) система уравнений:
b2+b5=84, b2+b5=84, b2+b5=84, b2+b5=84, b1*q+b1*q⁴=84,
b3+b6=252 b2*q+ b5*q=252 q(b2+b5)=252 q=252/84=3 q=3
b1(q+q⁴)=84, b1=84/(3+3*3*3*3)=84/(3+81)=84/84=1,
q=3 q=3.
теперь вычислим сумму первых 5 членов геом. прог.:
ответ: 121
1. Сократить дробь. (9а^2-4b^2) / (2b+3a)^2
знаки ^-возведение в степень
/-деление(дробь)
2. Решить систему уравнений. первое: 25х+2у=30 второе 5х-2у=-6
3. Найдите знаменатель геометрической прогрессии, если 30 ее член=31, а 31=32 4. Упростить: корень из 3,5 умноженный на корень из 2,1 делится как черта дроби на корень из 0,15
Решение: 1)(9a^2-4b^2)/(2b+3a)^2=(3a-2b)(3a+2b)/(2b+3a)^2 = (3a-2b)(2b+3a)2)
{25x+2y=50
{5x-2y=-6
{2y=50-25x
{5x-50+25x=-6
{30x=44
{x=22/15{y=20/3
3) b30=31
b31=32
q=b31/b30=32/31
4) V3.5*V2.1/V0.15=V49=7
По-другому...

Найдите знаменатель и первый член геометрической прогрессии, если произведение первого и третьего ее членов равно 9, а произведение второго и четвертого равно 81, причем, b1<0
q>0
Решение: В алгебре такое явление происходит редко, но так как оба составленных уравнения имеют одинаковые решения, то имеем право поделить их друг на друга(по степени выше на степень уравнения ниже), мы ничего в алгебре не нарушаем. Дальше вспоминаем условие и выражаем из второго b1(можно из первого, но арифм. действие посложнее чуток. Т. к. просят отрицательное b1, то извлекаем корень только с минусом.