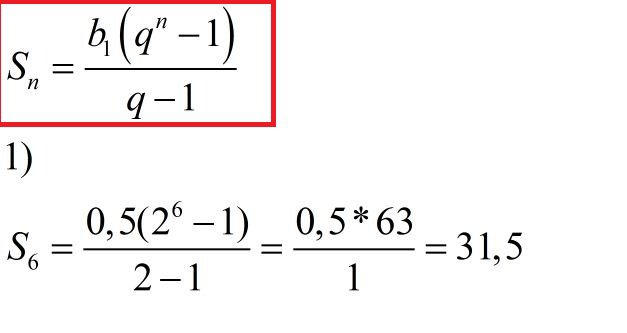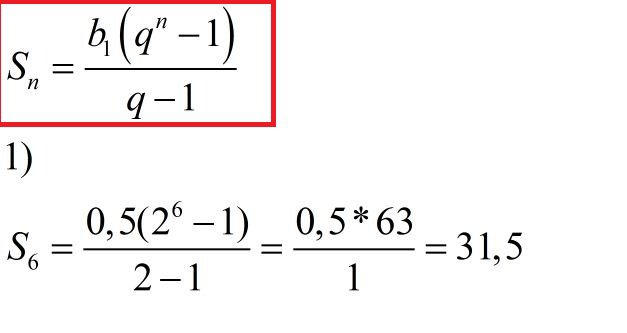прогрессия »

второй член геометрической прогрессии - страница 3

  • Составляют ли первый, второй и шестой члены арифметической прогрессии геометрическую прогрессию, если её третий член равен 7, а пятый 13


    Решение: $$ x_{1};x_{2};7;x_{4};13;x_{6};. $$-арифметическая прогрессия, составляют ли $$ x_{1};x_{2};x_{6} $$ - геометрическую прогрессию?

    Найдем разность арифметической прогрессии d=(13-7):2=3 Найдем первый, второй и шестой члены арифметической прогрессии

    $$ x_{1}=x_{3}-2d=7-6=1\\\\ x_{2}=x_{3}-d=7-3=4\\\ x_{6}=x_{1}+5d=1+5\cdot3=16 $$

    1;4;16;.=геометрическая прогрессия, потому что

    4:1=16:4

  • Является ли число 30 членом арифметической прогрессии -25; -19...?


    Решение:

     3) а1=-25 a2=-19

    d=a2-a1

    d=6

    a3=a2+d(3-1)

    a3=-19+12=-7

    a4=-7+18=11

    a5=11+24=35

    30 не является членом арифметической прогрессии.

  • найдите сумму первых восьми членов геометрической прогрессии второй член который равен 6 а четвертый равен 24


    Решение: Отношение их равно 4, корень квадратный (ведь две ступени) будет 2, значит члены равны: 
    b1=3

    b2=6

    b3=12

    b4=24

    b5=48

    b6=96

    b7=192

    b8=384 
    Следующий должен быть 768 
    Сумма членов двоичного ряда равна следующему за последним минус начальный (проверьте сами): 
    Сумма= 768-3=765. 

  • Найдите сумму первых шести членов геометрической прогрессии если первый её член меньше второго на 75 а сумма первых трёх равна 525


    Решение: Сумма n членов прогрессии
    S = b1 * (q^n - 1) / (q-1) = 81 * ((1/3)^6 - 1) / (1/3 - 1) = 121 и 1/3 (121,3333333.

    Сумма n членов прогрессии S b q n - q- - - и ....

  • Найдите сумму n первых членов геометрической прогрессии, если : 1) b1=1/2(одна вторая) q=2, n=6 3)b1=1, q=-1/3, n=4 5)b1=6, q=1,n=200


    Решение: Всё решается по формуле. Первый пример расписан, остальное - самостоятельноВс решается по формуле. Первый пример расписан остальное - самостоятельно...
<< < 123 4 5 > >>