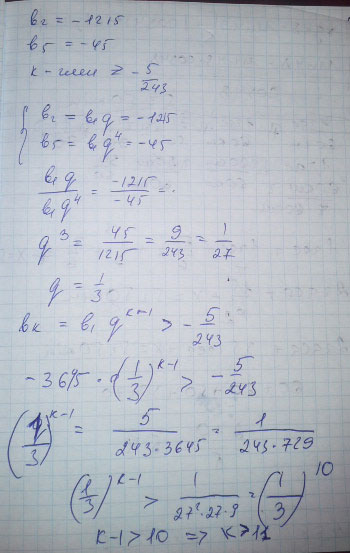прогрессия »

n член геометрической прогрессии - страница 25

  • В геометрической прогрессии известны члены a2 = –1215 и a5 = –45. Укажите номер k члена этой прогрессии, начиная с которого все её члены не меньше \( -\frac{5}{243} \)


    Решение: Очевидно что прогрессия убывающая 
    $$ b_{2}=-1215\\ b_{5}=-45\\ \\ b_{1}q=-1215\\ b_{1}q^4=-45\\ \\ q^3=\frac{45}{1215}=\frac{1}{27}\\ q=\frac{1}{3}\\ b_{1}=-3645 $$
    тогда по условию 
    $$ b_{n}>-\frac{5}{243}\\ b_{1}q^{n-1} > -\frac{5}{243}\\ -3645*\frac{1}{3}^{n-1} >-\frac{5}{243}\\ \frac{1}{3}^{n-1}<\frac{1}{177147}\\ \frac{1}{3}^{n-1}<\frac{1}{3^{11}}\\ (12;+oo) $$
    то есть начиная от 13 члена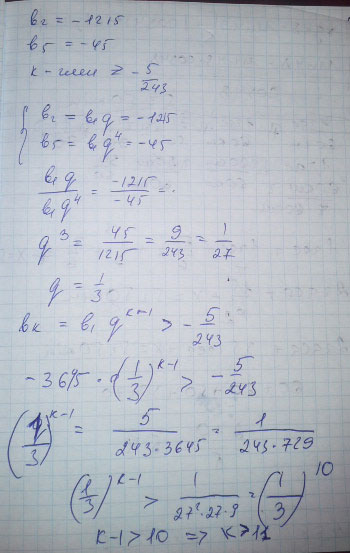 

    Очевидно что прогрессия убывающая  b - b - b q - b q - q frac frac q frac b - тогда по условию  b n - frac b q n- - frac - frac n- - frac frac n-...

  • В конечной геометрической прогрессии : а1; 0,72; а3; а4; 720; а6 известны некоторые члены. Найдите неизвестные члены данной прогрессии.


    Решение: \( {a_n} \)- геометрическая прогрессия
    $$ a_2=0.72 \\ a_5=720 \\ a_n=a_1* q^{n-1} \\ a_2=a_1*q \\ a_5=a_1*q^4 \\ \left \{ {{a_1*q=0.72} \atop {a_1*q^4=720}} \right. \\ \left \{ {{a_1*q=0.72} \atop {a_1*q*q^3=720}} \right. \\ \left \{ {{a_1*q=0.72} \atop {0.72*q^3=720}} \right. \\ \left \{ {{a_1*q=0.72} \atop {q^3=1000}} \right. \\ \left \{ {{a_1*q=0.72} \atop {q=10}} \right. \\ \left \{ {{a_1*10=0.72} \atop {q=10}} \right. \\ \left \{ {{a_1=0.072} \atop {q=10}} \right. \\ a_3=a_2*q=0.72*10=7.2 \\ a_4=a_3*q=7.2*10=72 \\ a_6=a_5*q=720*10=7200 $$
    Ответ: $${0.072;0.72;7.2;72;720;7200}$$

  • Найдите четвёртый член геометрической прогрессии, если b2=-2, b7=1/16


    Решение: Система двух уравнений с двумя неизвестными
    b₂ = b₁q = -2
    b₇ =  b₁q⁶ = \(\frac{1}{16} \\ ⇒ b₁q * q⁵ = \\ \frac{1}{16} \\ -2 * q⁵ = \\ \frac{1}{16} \\ q⁵ = - \frac{1}{32} \\  q = - \frac{1}{2} \)  $$b₄ = b₁q₃ = -2 * ( -\frac{1}{2})² =  - \frac{1}{2} $$ 

  • четвертый член геометрической прогрессии под корнем 3. Найдите произведение семи членов этой прогрессии.


    Решение: Сначала докажем некоторое равенство. Пусть известен элемент b_n = b1*q^(n-1). Тогда, зная его, можно найти произведение двух элементов b_(n-k) и b_(n+k), находящиеся на одинаковом расстоянии от b_n.
    b_(n-k) = b1 * q^(n-k-1)
    b_(n+k) = b1 * q^(n+k-1)
    b_(n-k) * b_(n+k) = b1 * q^(n-k-1) * b1 * q^(n+k-1) = b1^2 * q^(2n-2) = (b1*q^(n-1))^2 = b_n^2.
    Таким образом, зная лите b4, можно найти b3*b5=b4^2, b2*b6=b4^2 и b1*b7=b4^2. То есть b1*b2*b3*b4*b5*b6*b7=b4^7 = (√3)^7 = 27√3.

  • найдите пятый член геометрической прогрессии, в которой b3+b4=36, b2+b3=18


    Решение: Выразим каждый член через первый член геометрической прогрессии.
    $$ b_3=b_1*q^2; b_4=b_1*q^3; b_2=b_1*q $$ 
    Получим систему:
     $$ \left \{ {{b_1*q^2+b_1*q^3=36} \atop {b_1*q+b_2*q^2=18}} \right. \\ \left \{ {{b_1q^2(1+q)=36} \atop {b_1*q(1+q)=18}} \right. \\ \frac{b_1q^2(1+q)}{b_1q(1+q)} = \frac{36}{18} $$

    Сокращая дробь, мы получаем. 
    $$ q=2 $$ 

    Подставляем q в первое уравнение из системы: $$ b_1q+b_1q^2=18; q=2 \\ b_1=3 $$
    Следовательно, по формуле n-го члена геометрической прогрессии, получаем. 
    $$ b_5=3*2^4=48 $$ 
    Ответ: 48 

<< < 232425 26 27 > >>