сумма первых членов арифметической прогрессии - страница 3
Десятый член арифметической прогрессии равен -29, а сумма первых одиннадцати членов равна -187. Найдите сумму девятого, одиннадцатого и восемнадцатого членов этой прогрессии
Решение: 1. S(11) = (2a(1) + 10d)/2 * 11 = -187a(1) + 5d = -187/11 = -17
a(6) = -17
2. Составим систему уравнений: a(1) + 5d = -17
a(1) + 9d = -29
3. Следовательно d = -3, а a = -2, тогда
a(9) + a(11) + a(18) = 3*a(1) + 35d = - 6 - 105 = - 111
Ответ: - 111
Пятый член арифметической прогрессии равен 23, а восьмой член 35. найдите сумму первых десяти членов арифметической прогрессии.
Решение:Аn=а₁+ (n-1)д Определим дискриминант:
а₅=а₁+4д; откуда а₁=а₅-4д
а₈=а₁+7д; откуда а₁=а₈-7д; приравняем выражения для а₁:
а₅-4д=а₈-7д; а₈-а₅=7д-4д, 35-23=3д, д=4
Определим а₁ из любого выражения, например:
а₁= а₅-4·4=23-16=7;
также : а₁₀=а₁+9·4=43;
Σ=(а₁+а₁₀)·n:2=(7+47):5 =50·5=250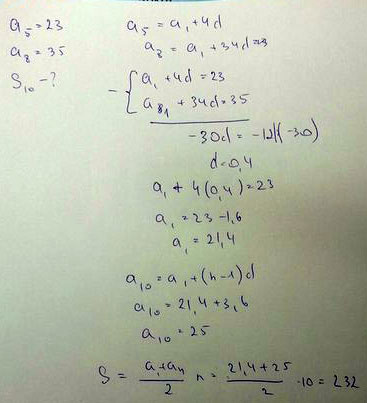
Десятый член арифметической прогрессии равен 17, а пятый член равен 4.
Найдите сумму пятнадцати первых членов этой прогрессии.
Решение: А10=а5+5d
а10- десятый член арифметической прогрессии
а5 - пятый член арифметической прогрессии
17=4+5d
5d=13
d=2,6 - разность прогрессии
а5=а1+4d
4=а1+4*2,6
а1= -6,4 - первый член арифметической прогрессии
По формуле выводим остальные члены арифметической прогрессии и получаем числовой ряд.
-6,3; -3,8; -1,2; 1,4; 4; 6,6; 9,2; 11,8; 14,4; 17; 19,6; 22,2; 24,8; 27,4; 30.
И вычисляем сумму, которая равна 177,1
1.1. 4-й член арифметической прогрессии равен 9, а 8-й член равен -7. сумма первых 5 членов прогрессии равна?
1.2. если 2-й и 5-й члены арифметической прогрессии равны 5 и 2 соответственно, то чему равно сумма первых 10 членов этой прогрессии?
1.3. 100-й член арифметической прогрессии равен 100, а 200-1 равен -100. найдите сумму членов этой прогрессии от 10-ого до 90-ого
2.1. в арифметической прогрессии 1-й член равен 33, разнность прогрессии равно -7, а сумма всех членов прогрессии 45. число членов в этой прогрессии равно?
2.2. если 3-й член арифметической прогрессии равен 9, 1-й член равен 5, а сумма n первых членов равна 165, то n равно?
2.3. найти число членов в прогрессии -10,14,18,406,410
Решение: 1.1. a8=a4+4dd=(-7-9)/4=-4 а1=21
s5=(2а1+4d)/2 *5=(42-16)/2 *5=65
1.2. a5=a2+3d
d=(2-5)/3=-1
a1=6
s10=(12-9)/2 *10=15
2.1.45=(66-7(n-1))/2 *n
90=66n-7n(n-1)
7n^2-73n+90=0 решите квадратное уравнение, найдете n (только положительное)
2.2. d=(9-5)/2=2
165=(5+2(n-1))/2 *n
330=5n+2n(n-1)
2n^2+3n-330=0 решите квадратное уравнение, найдете n (только положительное)
Первый член арифметической прогрессии равен 2, а десятый-десяти. Найти сумму десяти членов этой прогрессии.
Решение: Если х2 это второй член арифметической прогрессии, то это решается так:
Sn - сумма членов арифметической прогрессии
Sn= n(a1 + a2)/2
Находим первый член арифметической прогрессии: a2 - d = а1
-2 - 1,2 = -3,2
n = 10
S10 = 10(-3,2 - 2)/2 = -26
Ответ: -26сумма равен (а1+а10)n/2= (2+10)10/2=60