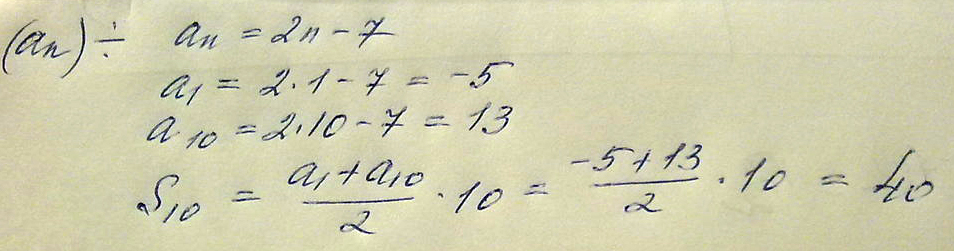прогрессия »
сумма первых членов арифметической прогрессии - страница 37
Арифметическая прогрессия (An) задана формулой An=10-4n Сколько членов этой прогрессии, начиная с первого, сложили если в сумме получилось -120 ?
Решение: Найдем через формулу прогрессии 1 член:
$$ a_1=10-4=6 $$
Формула суммы через первый и последний член суммы:
$$ S_n= \frac{n(a_1+a_n)}{2} $$
Подставим нашу сумму:
$$ -120= \frac{n(6+a_n)}{2} $$
Мы знаем чему равен $$ a_n $$:
$$ -120= \frac{n[6+(10-4n)]}{2} $$
Теперь решим как обычное уравнение:
$$ -120= \frac{n(16-4n)}{2} $$
$$ -240=16n-4n^2 $$
$$ -4n^2+16n+240=0 $$
$$ 4(-n^2+4n+60)=0 $$
$$ -n^2+4n+60=0 $$
$$ \sqrt{D}= \sqrt{16+240}= \sqrt{256}=16 $$
$$ n_{1,2}= \frac{-4\pm16}{-2}=10,(-6) $$
Но наша задача узнать номер количества. А он не может быть отрицательным. Поэтому, подходит только n=10.арифметическая прогрессия(аn) задана условием аn=2n-7. найти сумму первых десяти членов прогрессии
Решение: Формула суммы арифметической прогрессии:Sn = (a1 + an) / 2 * n, где:
a1 = 2 * 1 - 7 = -5
a10 = 2 * 10 - 7 = 13
S10 = (-5 + 13) / 2 * 10 = 40.
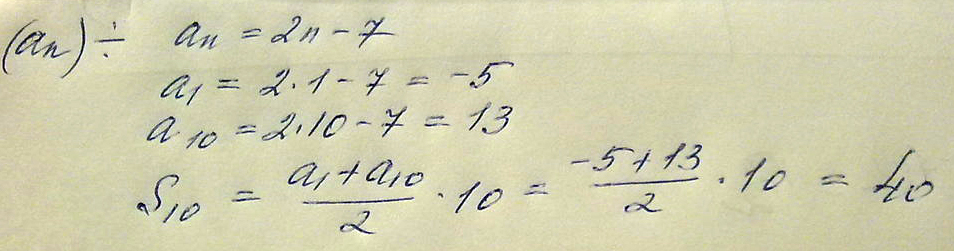
1. Найдите сумму тридцати первых членов арифметической прогрессии, заданной формулой аn = Зn + 2.
2. В арифметической прогрессии а6 = 1 и а10 = 13. Найдите сумму первых двадцати членов.
3. Найдите сумму всех трехзначных чисел, кратных 4.
Решение: 1)
a30=3*30+2
a30=92
3)
На 4 делятся такие числа, которые заканчиваются на 00 или 2 последних числа делятся на 4.
так же с помощью арифметической прогрессии.
наименьшее 100, наибольшее 996
вспомним формулу для нахождения суммы и подставим наши числа.
(а1+(a1+d*(n-1)))*n/2=100004
арифметическая прогрессия (an) задано условием: an=1.4+0.3n. найдите сумму первых семнадцати членов прогрессии
Решение: Нам известна формула:a(n)=a1+d*(n-1); Где a(n) - n-ый член прогрессии, a1 - первый член прогрессии, d - разность.
И нам известно условие: a(n)=1,4+0,3n.
Из условия найдем первый и 17 член прогрессии.
a(1)=1,4+0,3*1=1,4+0,3=1,7.
a(17)=1,4+0,3*17=1,4+5,1=6,5.
Теперь запишем формулу для суммы n первых членов арифметической прогрессии:
$$ S(n)=\frac{(a1+a(n))*n}{2};\\ $$
Данные нам известны, подставляем и считаем:
S(17)=((1,7+6,5)*17)/2=69,7.
Ответ: S(17)=69,7.
Арифметическая прогрессия.
Второй член прогрессии равен 5. Найдите сумму первых трех членов прогрессии.
Решение: А-арифметическая прогрессия. нам надо найти сумму первых трех членов данной прогрессии, т. е.S=a1+a2+a3.
арифметической прогрессии свойственно следующее характеристическое саойство:
An=((An-1)+(An+1)):2, какой либо член арифметической прогрессии равен полусумме предыдущего его члена и следующего.
зн. в данном случае а2=(а1+а3):2
зн.5=(а1+а3):2.> а1+а3=10,
S=а1+а2+а3=(а1+а3)+а2=10+5=15
Ответ: 15