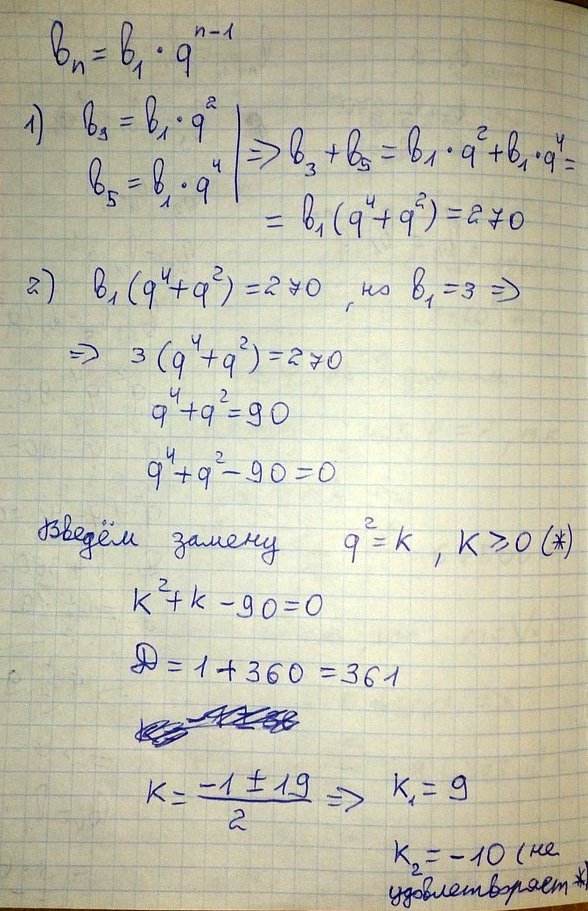в геометрической прогрессии первый член равен - страница 31
В знакочередующейся геометрической прогрессии первый член равен 3, а сумма третьего и пятого членов равна 270. Найдите четвертый член прогрессии?
Решение: Сумма третьего и пятого членов:S = b1(q^2 + q^4) = 60
q^2 + q^4 = 20
q^4 + q^2 - 20 = 0. По теореме Виета находим возможные значения q^2:
q^2 = -5 - не подходит
q^2 = 4 значит q = -2 ( по условию знакопеременности).
Тогда b2 = b1*q = - 6.
Ответ: - 6
. Ответ на фото.
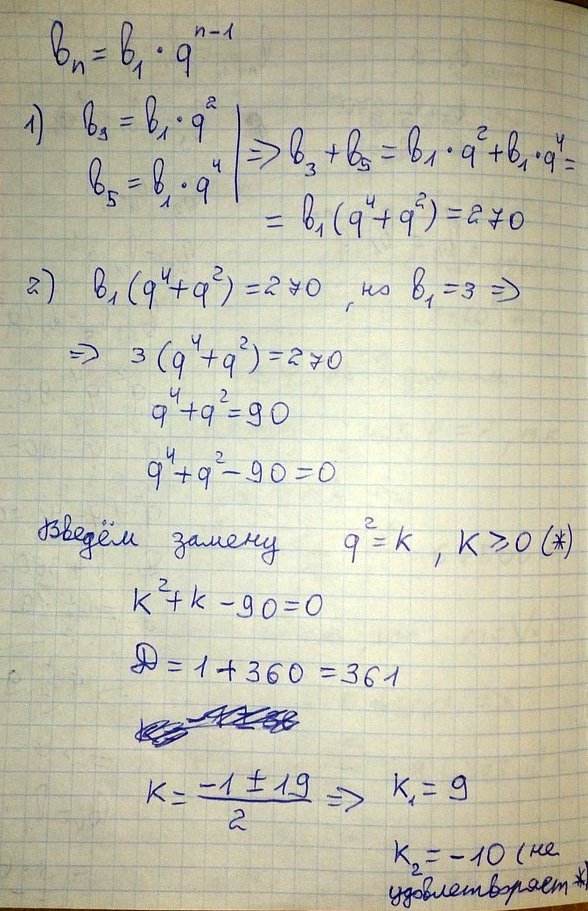
Найдите сумму первых шести членов знакопеременной геометрической прогрессии ЕСЛИ ПЕРВЫЙ ЧЛЕН РАВЕН 2, А ТРЕТИЙ -8
Решение: Находим знаменатель прогрессии:
$$ b_1=2\\b_3=b_1*q^2=-8\\\frac{b_1q^2}{b_1}=\frac{-8}{2}\\q^2=-4 $$
Получаем неверное равенство. Задача не имеет решения.$$ b_1=2 $$
$$ b_3=-8 $$
$$ b_n=q*b_{n-1}=q^2*b_{n-2} $$ ⇒
$$ b_3=q^2*b_{1} $$
Значит, $$ q^2= \frac{-8}{2} eq -4 $$ - неверное равенство.
Ответ: нет решении для данной задачи.
Найти сумму первых семи членов геометрической прогрессии, если третий член равен 8, а шестой 64
Решение: Уравнение геометрической прогрессии:
an = a1*q ^(n-1)
На основе данных задания записываем:
8 = a1*q²
64 = a1*q⁵.
Разделим второе уравнение на первое.
8 = q³
q = ∛8 = 2.
Из 1 уравнения получаем а1 = 8/q² = 8/2² = 8/4 = 2.
Сумма Sn = (an*q - a1) / (q - 1).
Для этого надо найти 7 член прогрессии:
a7 = 2*2(7-1) = 2*2⁶ = 2*64 = 128.
Тогда S7 = (128*2 - 2) / (2 - 1) = 256 - 2 = 254.
Первый член геометрической прогрессии равен 1 сумма третьего и пятого членов равен 90 найдете сумму первых пяти членов прогрессии.
Решение: Так как первый член прогрессии равен 1, формула для n-ного члена будет h^(n-1), где h - шаг (множитель) прогрессии.
Третий член - это h^2
Пятый член - это h^4
Сумма 3-го и 5-го членов:
h^2 + h^4 = 90
Отсюда:
h^2 * (1+h^2) = 90
такое возможно только при h=3: 9*10=90
Поэтому имеем прогрессию: 1, 3, 9, 27, 81,
Сумма 5-ти первых членов равна 121Если в геометрической прогрессии третий член положителен, четвертый член равен -4, а сумма третьего и шестого членов равна -14, то сумма первого члена и знаменателя прогрессии
Решение: B3 + b6 = -14, b1*q^2 + b1*q^5 = -14, b4 = -4, => b1*q^3 = -4,=> b1 = -4/q^3
Подставим b1. в первое уравнение:
-4/q - 4q^2 = -14 | * ( - q / 2), т. к q не равно 0
2 + 2q^3 - 7q = 0 | разложим по теореме Безу, методом подбора корень -2
( q + 2 )( 2q^2 - 4q + 1 ) = 0, q2 = 1 - 1/ корень 2, q3 = 1 + 1/корень2 ( оба не подходят, т. к по условию q < 0)
b1 * (-2)^3 = - 4
b1 = 1/2
b1 + q = 1/2 - 2 = -3/2
Вот решение.
b₄ = -4
b₃ + b₆ = -14
b₄ = b₁*q³
b₃ = b₁*q²
b₆ = b₁*q⁵
b₁*q³ = -4
b₁*q² + b₁*q⁵ = -14
b₁ = $$ - \frac{4}{ q^{3} } $$
$$ - \frac{4* q^{2} }{ q^{3} } - \frac{4* q^{5} }{ q^{3} } = -14 $$
$$ - \frac{4}{q}-4 q^{2} = -14 $$
-4 - 4q³ = -14q
-4q³ + 14q - 4 = 0
4q³ - 14q + 4 = 0
2q³ - 7q + 2 = 0
q = -2
b₁ = $$ \frac{4}{ 2^{3} }= \frac{4}{8} = \frac{1}{2} $$
b₁ + q = $$ \frac{1}{2}-2 = -1 \frac{1}{2} $$
Ответ: $$ -1 \frac{1}{2} $$