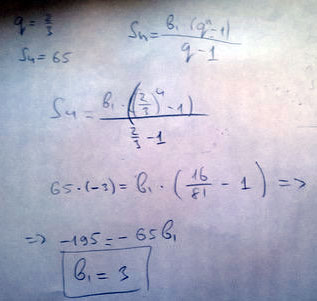в геометрической прогрессии первый член равен - страница 48
Найти пятый и первый члены геометрической прогрессии с положительными членами, если:
b4=1/27
b6=1/3
Решение: b₄=b₁*q³;b₆=b₁*q⁵;
b₁= b₄/q³;
b₁=b₆/q⁵;
b₄/q³=b₆/q⁵;
b₄=b₆/q²;
1/27=1/3/q²;
q²=1/9;
q₁=1/3;
q₂-=-1/3;
b₅=b₄*q=1/27*(1/3)=1/81; или b₅=b₄*q=1/27*(-1/3)=-1/81.
b₁=b₆/q⁵=1/3/(1/243)=81; или b₁=b₆/q⁵=1/3/(-1/243)=-81.
ОТВЕТ: -1/81; -1/81; 81; -81.
Найти сумму первых 7 членов геометрической прогрессии в которой B2 равен 6 и B4 равен 54 все ее члены положительны
Решение: B2=6
b4=54
S(7)-
b1-
q-
b2=b1*q
b4=b1*q^3
b1*q=6
b1*q^3=54
6q^2=54
q^2=9
q=3
b1=6/q
b1=2
S(n)=b1(q^(n)-1)/q-1
S(7)=2(3^7-1)/3-1=2186
Ответ:2186Вычисляем
B2 = b1*q B4= B1*q³ B4/B2= q² = 54/6 = 9 q= √9 = 3
B1= B2/q = 6/3 = 2.
Сумма первых семи членов
S7 = B1*(1+3+9+27+81+243+729) =2*1093 = 2186
ОТВЕТ: Сумма семи членов 2186.Вычислите первый член геометрической прогрессии, если ее седьмой член равен 80, а пятый 20
Решение: находим первый член геометрической прогрессиикак известно по определению n-й член прогресси равен
$$ a_{n}=a_{1}*q $$
где $$ a_{1} $$ - первый член прогресси (который нужно найти)
q- знаменатель прогрессии.
Составим следующую систему уравнений, используя данный условия задачи - значения 5-го и 7 членов$$ \left\{ \begin{array}{l l} a_{5}= a_{1}*q^{5-1} \\ a_{7}= a_{1}*q^{7-1} \ \end{array} \right.\Rightarrow \left\{ \begin{array}{l l} 20= a_{1}*q^{4} \\ 80= a_{1}*q^{6} \ \end{array} \right.\Rightarrow\left\{ \begin{array}{l l} a_{1}=\frac{20}{q^{4}} \\ 80= \frac{20}{q^{4}}*q^{6} \ \end{array} \right.\Rightarrow \\ \left\{ \begin{array}{l l} a_{1}=\frac{20}{q^{4}} \\ q^{2}=4 \ \end{array} \right.\Rightarrow\left\{ \begin{array}{l l} a_{1}=\frac{20}{16} \\ q=\pm2 \ \end{array} \right.\Rightarrow\left\{ \begin{array}{l l} a_{1}=\frac{5}{4} \\ q=\pm2 \ \end{array} \right.\Rightarrow $$
ответ $$ a_{1}=\frac{5}{4} $$
Найдите первый член геометрической прогрессии, в которой q=2/3,S4=65
Решение: S₄ =b₁(1-q⁴)/(1-q) ⇒b₁ =S₄(1-q)/(1-q⁴) ;
b₁ =65(1-2/3)/(1-2/3)⁴) =(65/3)/(65/81)81/3=27.
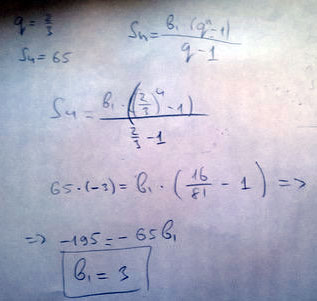
№1) Найти сумму первых членов геометрической прогрессии если:
1)b1=5; g=-1; n=9
2) b1=2; g=2; n=5
3)b1=1/8; g=5; n=4
№2) Найти сумму чисел если её слогаемые являются последовательными членами геометрической прогрессии
1/4+1/8+1/16+.+1/512
Решение: №1
общая формула S(n) = b1*(q^n -1)/(q-1)
1)b1=5; g=-1; n=9
S(9) = 5*((-1)^9 -1)/((-1)-1) = 5
2) b1=2; g=2; n=5
S(5) = 2*(2^5 -1)/(2-1) = 62
3)b1=1/8; g=5; n=4
S(4) = 1/8*(5^4 -1)/(5-1) = 39/2 или 19.5
№2)
знаменатель прогрессии q =1/8 / 1/4 = 4/8 =1/2
b1 = 1/4 ; bn = 1/512
сумма -n- членов S(n)
S(n)= (bn*q -b1)/ (q-1)=((1/152)*(1/2) -1/4) / (1/2-1)= 75/152
№1) Найти сумму первых членов геометрической прогрессии если:1)b1=5; g=-1; n=92) b1=2; g=2; n=53)b1=1/8; g=5; n=4
Sn=b1(1-q^n)/(1-q) если q<>1
b1- рервый член
q- коэффициент
1. Sn=5(1-(-1)^9)/(1-(-1))=5*2/2=5
2. Sn=2(1-2^5)/(1-2)=2*(-31)/(-1)=62
3. Sn=1/8(1-5^4)/(1-5)=1/8*(-624)/(-4)=39/2
№2) Найти сумму чисел если её слогаемые являются последовательными членами геометрической прогрессии 1/4+1/8+1/16+.+1/512
b1=1/4
q=1/2
bn=1/512
Sn=(bn*q-b1)/(q-1)=(1/512*1/2-1/4)/(1/2-1)=(-255/1024)/-1/2=255/512