разность членов арифметической прогрессии - страница 4
В арифметической прогрессии пятый член равен 2. при каком значении разности прогрессии сумма всевозможных попарных произведений четвертого, седьмого и восьмого членов прогрессии будет наименьшей?
Решение: В рекурентной форме пятый член арифметической прогресси выглядит как: a5=a1+4d=2, выразим а1: a1=2-4dТеперь в рекурентной форме выразим a4, a7, a8:
a4=a1+3d; a7=a1+6d; a8=a1+7d
Составим всевозможные попарные произведения этих членов прогрессии:
1) a4*a7=(a1+3d)(a1+6d)=(2-4d+3d)(2-4d+6d)=(2-d)(2+2d)=-2d^2+2d+4
2)a4*a8=(a1+3d)(a1+7d)=(2-4d+3d)(2-4d+7d)=(2-d)(2+3d)=-3d^2+4d+4
3)a7*a8=(a1+6d)(a1+7d)=(2-4d+6d)(2-4d+7d)=(2+2d)(2+3d)=6d^2+10d+4
Найдем сумму этих произведений:
S=a4*a7+ a4*a8+a4*a8=-2d^2+2d+4-3d^2+4d+4+6d^2+10d+4=d^2+16d+12
Зададим формулу суммы в виде функции:
y(d)=d^2+16d+12, это функция квадратичная её графиком является парабола, т. к. коэффициент при d^2 положительный, то минимальное значение функция будет принимать в вершине параболы=> для того чтобы найти нужное нам значение d (такое чтобы сумма была минимальной), нам необходимо найти координату вершины параболы на оси Ох, для этого воспользуемся формулой х0=-(b/2a), т. к. у нас d вместо х, то d0=-(b/2a)=-(16/2)=-8, это и есть то значение разности прогрессии при котором, сумма всевозможных попарных произведений чевертого, седьмого и восьмого членов прогрессии будет наименьшей. Можно даже вычислить его, для этого подставляем d0 в уравнение функции, получаем:
yнаим.=(-8)^2-128+12=-52, т. е. Sнаим.=-52.
Ответ: d=-8; Sнаим.=-52
В арифметической прогрессии второй член равен 3, а сумма 18 первых членов равна 1539. Найдите разность этой прогрессии.
Решение: В арифметической прогрессии второй член равен 3, а сумма 18 первых членов равна 1539. Найдите разность этой прогрессии.
a2=a1+d=3 a1+d=3
S18=[(2·a1+17·d)/2]·18 =1539 ⇒ 18·a1+153d=1539
18·a1+18·d=54
18·a1+153d=1539 ⇒135·d=1485 ⇒ d=1485/135 d=11
В арифметической прогрессии третий член равен 9, а разность равна 20. найдите тридцатый член этой прогрессии
Решение: a3=9d=20
a30-
an=a1+d(n-1)
a3=a1+20*2
a1+40=9
a1=9-40
a1=-31
a30=a1+29d=-31+29*20=-31+580=549
====================================
Запишем формулу для нахождения тридцатого члена арифметической прогрессии:
a30 = a1 + 29d
Мы не знем лите первый член прогрессии. Найдём его, зная третий член:
a3 = a1 + 2d
a1 = a3 - 2d = 9 - 40 = -31
Теперь без проблем ищем тридцатый член:
a30 = -31 + 29 * 20 = -31 + 580 = 549
Задача решена.
В арифметической прогрессии второй член равен 4, разность рав-на 3, а сумма первых n членов прогрессии равна 376. Найдите n.
Решение: Если второй член = 4 и разность равна 3, то цепочка выглядит так:
1, 4, 7, 10, 13.
=> по формуле (прикреплена) получаем n = 16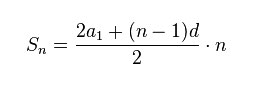
Найдите разность арифметической прогрессии, первый член которой равен 10, а сумма первых пятнадцати членов равна 1200.
Решение: S15=2a1+d(15-1)
_________________x15
2
S=20+14d
__________x15
2
S=2(10+7d)
_________x15
2
S=(10+7d)x15=1200
150+105d=1200
105d=1050
d=10