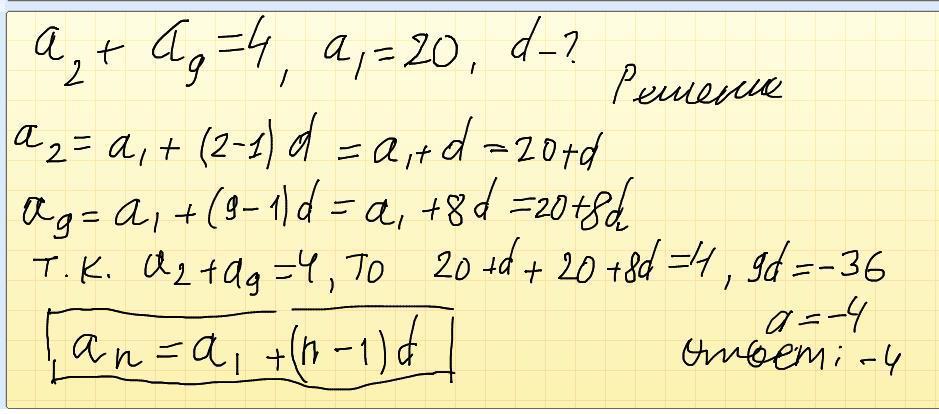прогрессия »
разность членов арифметической прогрессии - страница 6
Вычислите сумму пятнадцати первых членов арифметической прогрессии, если ее шестой член равен 2,2, а разность равна 2,4.
Решение: Энный член арифметической прогрессии равен:
$$ a_n=a_1+d(n-1). $$
Отсюда первый член прогрессии равен:
$$ a_1=a_n-d*(n-1)=2,2-2,4*(6-1)=2,2-12=-9,8. $$
Пятнадцатый член равен:
$$ a_{15}=-9,8+2,4*14=23,8. $$
Сумма пятнадцати первых членов арифметической прогрессии равна:
$$ S_{n}= \frac{(a_1+a_n)*n}{2} = \frac{(-9,8+23,8)*15}{2} =105. $$
А) В арифметической прогрессии с разностью d девятый член равен 1. При каком значении d произведение четвертого, седьмого и восьмого членов прогрессии будет наибольшим?
б) В арифметической прогрессии с разностью d второй член равен 6. При каком значении d произведение первого, третьего и шестого членов будет наименьшим?
Решение: A9 = a1 + 8*d = 1
a4 * a7 * a8 = (a1 + 3d) * (a1 + 6d) * (a1 + 7d) =
= (a1 + 3d+5d-5d) * (a1 + 6d+2d-2d) * (a1 + 7d+d-d) =
= (1 - 5d) * (1 - 2d) * (1 - d) = (1 - 7d + 10d²) * (1 - d) =
= 1 - 8d + 17d² - 10d³
производная = -30d² + 34d - 8 = 0 (условие нахождения экстремума)
15d² - 17d + 4 = 0
D=17² - 16*15=7²
d = (17 - 7) / 30 = 1/3 или
d = (17 + 7) / 30 = 24/30 = 4/5 = 0.8
если d=0 значение производной -8 < 0
если d=1/2 (10/30 <15/30 < 24/30) значение производной
-(30/4) + (34/2) - 8 = -7.5 + 17 - 8 = -15.5+17 > 0
если d=1 значение производной -30 + 34 - 8 < 0
следовательно, точка максимума: d = 0.8
-
a2 = a1 + d = 6
a1 * a3 * a6 = a1 * (a1 + 2d) * (a1 + 5d) =
= a1 * (a1 + d+d) * (a1 + d+4d) =
= (6 - d) * (6 + d) * (6 + 4d) = (36 - d²) * (6 + 4d) = 6*36 +144d - 6d² - 4d³
производная = -12d² - 12d + 144 = 0 (условие нахождения экстремума)
d² + d - 12 = 0
по т. Виета корни (-4) и (3)
если d=-5, производная = -300+204 < 0
если d = 0, производная = 144 > 0
если d=4, производная = -192-48+144 < 0
d = -4 -это точка минимума))
В арифметической прогрессии разность равна (-7), а двенадцатый член равен 46. Найдите количество положительных членов?
Решение: $$ d=-7;a_{12}=46 $$
$$ a_n=a_1+(n-1)*d $$
$$ a_1=a_n-(n-1)*d $$
$$ a_1=46-(12-1)*(-7) $$
$$ a_1=123 $$
$$ a_n>0 $$
$$ 123+(n-1)*(-7)>0 $$
$$ 123-7n+7>0 $$
$$ 130>7n $$
$$ 7n<130 \\ n<\frac{130}{7}=18\frac{4}{7} $$ максимальное натуральное n удовлетворяющее неравенство 18
Ответ: 18 положительных членов
В арифметической прогрессии сумма первых восьми членов равно -312, сумма семи членов той же прогрессии -266 и разность -2. Чему равен первый член прогрессии?
Решение: ДАНО
S8=312
S7=266
d=2
НАЙТИ
а1=?
РЕШЕНИЕ
S7-=a8= 312-266 = 46
a8 = a1 + 7*d = 46
a1 = 46-14 = 32
ОТВЕТ: Первый член прогрессии = 32.
При отрицательных значениях сумм и разности прогрессии значение а1= - 32
Значения промежуточных челнов на рисунках.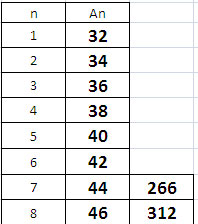
Если в арифметической прогрессии сумма второго и девятого членов равна 4, первый член равен 20, то разность прогрессии равна ...
Решение: Применим формулу нахождения n- го члена арифметической прогрессии для второго и девятого
Используя условия задания, составим уравнение и решаем его