прогрессия »

найти следующие числа арифметической прогрессии - страница 3

  • Числа а1, а2, а3 составляют арифметическую прогрессию а их квадраты - геометрическую. Найти эти числа если а1+а2+а3=21.


    Решение: Искомую тройку чисел a1 a2 a3 запишем в виде: a-d, a, a+d следовательно 21=(a-d)+a+(a+d)=3a следовательно a=7.

    Так как числа (7-d)^2,7^2, (7+d)^2 образуют геометрическую прогрессию то:

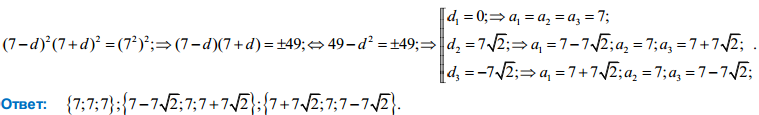
    Искомую тройку чисел a a a запишем в виде a-d a a d следовательно a-d a a d a следовательно a . Так как числа -d d образуют геометрическую прогрессию то...

  • Цифры каждого из трех трехзначных чисел составляют арифметическую прогрессию, сумма этих чисел 750. Найти трехзначные числа.


    Решение: 100a+10(a+d)+a+2d+100b+10(b+k)+b+2k+100m+10(m+n)+m+2n=750
    111(a+b+m)+12(d+k+n)=750
    a>0;b>0;m>0; a,b,m, Цифры, от 0 до 9
    d,k,n - целые от -4 до 4 (шаг)
    -12<=d+k+n<=12
    750-111*1 нацело на 12 не делится
    750-111*2 нацело на 12 делится d+k+n=750:12=44>12
    750-111*3 нацело на 12 не делится
    750-111*4 нацело на 12 не делится
    750 -111*5 нацело на 12 не делится
    750-111*6 нацело на 12 делится d+k+n=750:12=7
    750-111*7 нацело на 12  не делится
    750-111*8  не делится
    750-111*9 нацело на 12  не делится
    750-111*10 нацело на 12 делится  d+k+n=-30<-12
    значит a+b+m=6; d+k+n=7
    а теперь самое веселое с точностью до перестановки слагаемых
    a=1 b=1 m=4 ;
    a=1 b=2 m=3 
    a=2 b=2 m=2
    d=0 k=0 n=7
    d=0 k=1 n=6
    d=0 k=2 n=5
    d=0 k=3 n=4
    d=1 k=1 n=5
    d=1 k=2 n=4
    d=1 k=3 n=3
    d=2 k=2 m=3
    первое число 111*a+12*d
    второе число 111*b+12*k
    третье число 111*n+12*m
    например серия a=1 b=1 m=4 ; и d=0 k=0 n=7
    получим числа 111+111+528=750
    всего таких троек будет 3*8=24

  • Числа, которые выражают длины сторон прямоугольного треугольника, создают арифметическую прогрессию. меньший катет равен a. найти площадь треугольника


    Решение: Меньший катет = а
    больший катет = а+d
    гипотенуза = a+2d
    d - разность прогрессии
    прогрессия возрастающая
    по теореме Пифагора: (a+2d)^2=(a+d)^2+a^2
    3d^2+2ad-a^2=0
    Решаем квадратное уравнение относительно переменной d.
    D=16a^2
    d1=a/3  d2=-a (не подходит, т. к. прогрессия возрастающая)
    S=1/2 * a * (а+d) =1/2 * a * (а+a/3) = (2*a^2)/3
    Ответ:(2*a^2)/3

  • Требуется найти 3-значное число. Его цифры образуют арифметическую прогрессию. Если из него вычесть 792, то получится число, записанное теми же цифрами, что и искомое, но в обратном порядке. Если же из цифры десятков искомого числа вычесть 2, а остальные не трогать, то получится число, цифры которого образуют геометрическую прогрессию.


    Решение: Нужно составить систему, пусть у этого числа х, у,z - соответственно число сотен, десятков и единиц 
    100х+10у+z-792=100z+10y+x 
    y-x=z-y 
    (y-2)/x=z/(y-2) 
    x-z=8 
    x+z-2y=0 
    xz=(y-2)^2 
    Так как число сотен должно быть меньше 10, то возможны 2 варианта 
    1) х=8, z=0 
    Система не совместна 
    2) х=9, z=1 
    y=(x+z)/2=10/2=5 
    Ответ: 951.

  • Три числа образуют геометрическую прогрессию. Если второе число увеличить на 8, то прогрессия станет арифметической. Но если после этого увеличить последнее число на 64, то прогрессия снова сделается геометрической. Найти эти числа.


    Решение: $$ b_n=[a, b, c]\\b/a=c/b\\\\a_n=[a, b+8, c]\\b+8-a=c-b-8\\\\b_{n_2}=[a, b+8,c+64]\\(b+8)/a=(c+64)/(b+8)\\\\ a=16+2b - c\\c=b^2/a\\b+8=a(c+64)/(b+8)\\(b+8)^2=a(c+64)\\ca=b^2\\b^2+16b+64=b^2+64a\\16b+64-64a=0\\16(b+4-4a)=0\\b+4-4a=0\\b=4a-4\\\\4a-4+8-a=c-4a+4-8\\7a+8-c=0\\7a+8-b^2/a=0\\7a^2+8a-b^2=0\\7a^2+8a-(4a-4)^2=0\\7a^2+8a-(16a^2-32a+16)=0\\-9a^2+40a-16=0\\9a^2-40a+16=0\\a_1=4/9\\a_2=4.\\\\1) a=4\\b=12\\c=36.\\\\2) a=4/9\\b=16/9-4=-20/9\\c=100/9. $$
    Ответ: 4, 12, 36, либо $$ \frac{4}{9}, \frac{-20}{9}, \frac{100}{9} $$.
<< < 123 4 5 > >>