первообразная »

найдите первообразную для функции - страница 4

  • Для функции f(x)=sin3x найдите первообразную, график которой проходит через данную точку А(п/3;1/3)


    Решение: Находим интеграл $$ \int{sin3x} \, dx =- \frac{1}{3}cos3x+C $$/
    Поскольку график полученной функции проходит через точку А, то координаты этой точки должны удовлетворять наше уравнение F(x)=-1/3cos3x+C. Подставим координаты данной точки $$ \frac{1}{3}=- \frac{1}{3}cos3* \frac{ \pi }{3} +C $$.
    Откуда С=0. Имеем первообразную $$ F(x)=- \frac{1}{3}cos3x $$

  • Для функции y=f(x) найдите первообразную F(x), график которой проходит через точку M(a;b), если: \( f(x)=x^{-3}+cosx, х∈(0;\infty), M(0,5\pi; - \frac{1}{2 \pi ^{2}}) \)


    Решение: Для функции y=f(x) найдите первообразную F(x)? график которой проходит через точку М(а;b), если: $$ f(x)=x^{-3}+cosx $$, где х∈(0;oo),M(0,5π;$$ - \frac{1}{2 \pi ^{2}} $$);
    Решение:
    Найдем первообразную

    $$ F(x)= \int {(x^{-3}+cosx)} \\ dx = \int {x^{-3}} \\ dx+ \int {cosx} \, dx = -\frac{1}{2}x^{-2}+sinx+C $$

    Найдем значение С подставив значение координат точки М в уравнение первообразной

    $$ F(x)= -\frac{1}{2}x^{-2}+sinx+C $$

    $$ -\frac{1}{2}( \frac{ \pi}{2})^{-2}+sin( \frac{ \pi }{2})+C =- \frac{1}{2 \pi^{2} } $$

    $$ -\frac{2}{\pi^{2}}+1+C = - \frac{1}{2 \pi^{2} } $$

    $$ C =\frac{2}{\pi^{2}}-\frac{1}{2 \pi^{2} }+1 $$

    $$ C = \frac{3}{2\pi^{2}} -1 $$

    Запишем уравнение первообразной функции f(x) проходящей через точку М

    $$ F(x)= -\frac{1}{2}x^{-2}+sinx+ \frac{3}{2\pi^{2}} -1 $$

  • 3. Для функции f(x)=2x-2 найдите первообразную F график
    которой проходит через A(2:1)



    4. Точка движется по прямой так что её скорость в момент
    времени t равна V(t)=3+0,2t
    Найдите путь пройденный точкой за время от 1 до 7секесли
    скорость измеряется в м/сек.



    5 Найдите площадь криволинейной трапеции ограниченной
    линиями y=2x^2, y=0 x=2


    Решение: 3. Для функции f(x)=2x-2 найдите первообразную F график
    которой проходит через A(2:1)
    F(x)=x²-2x+C
    Подставляем координаты точки А
    1=2²-2*2+C
    С=1
    Ответ: x²-2x+1

    4. Точка движется по прямой так что её скорость в момент
    времени t равна V(t)=3+0,2t
    Найдите путь пройденный точкой за время от 1 до 7 сек, если скорость измеряется в м/сек.
    Поскольку скорость есть производная от пути, то путь - первообразная.
    $$ s= \int\limits^7_1 {3+0.2t} \, dt =3t+0.1t^2|_1^7=3*7+0.1*7^2-3*1-0.1*1^2= \\ =21+4.9-3-0.1=22,8 $$
    Ответ: 22,8 м

    5 Найдите площадь криволинейной трапеции ограниченной
    линиями y=2x^2, y=0 x=2
    $$ S= \int\limits^2_0 {2x^2} \, dx = \frac{2x^3}{3} |_0^2= \frac{2*2^3}{3}= \frac{16}{3}=5 \frac{1}{3} $$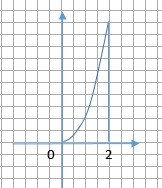. Для функции f x x- найдите первообразную F графиккоторой проходит через A F x x - x CПодставляем координаты точки А - CС Ответ  x - x . Точка движется по прямой так что е с...

  • Для функции f(x)=2/(Sin^2 3x), найдите первообразную, график которой проходит через точку М(pi/6;3)


    Решение: Для функции f(x)=2/(Sin^2 3x), найдите первообразную, график которой проходит через точку М(pi/6;3)
    Решение:
    Найдем интеграл функции f(x)=2/(sin^2(3x))
    F(x)=$$ int\ { \frac{2}{sin^2(3x)}} \, dx= \frac{2}{3} \int\ { \frac{1}{sin^2(3x)}} \, d(3x)=-\frac{2}{3}ctg(3x)+C $$
    Найдем значение константы С подставив координаты точки М(pi/6;3)
    $$ -\frac{2}{3}ctg(3* \frac{\pi}{6} )+C=3 $$
    $$ -\frac{2}{3}ctg(\frac{\pi}{2} )+C=3 $$
    C=3
    Поэтому можно записать, что
    F(x)=-(2/3)ctg(3x)+3

  • Для функции \( f(x)=\frac{3}{5+3x} \) найдите первообразную на промежутке (\( -\frac{5}{3} \); +\( \infty \))


    Решение: f(x)=3/(5+3x)
    F(x)=F(3/(5+3x))=3F(1/(5+3x))=3*1/3 * ln|5+3x| + C = ln|5+3x|+C
    Так как x = (-5/3;+беск), то |5+3x|=5+3x

    => F(x)=ln(5+3x)+C 

    Для начала найдем первообразную функции на всей числовой прямой:

    $$ \int{\frac{3}{5+3x}}\, dx=ln|5+3x|+C $$

     Знак модуля ставится ввиду того, что производная от модуля существует как в отрицательном значении, так и положительном, но так как задан промежуток интегрирования, на котором интегрируема функция получаем:

    $$ 5+3x=0 $$

    $$ x=-\frac53 $$

    Получаем, что в данном промежутке произвадная существует только при положительном значении модуля, поэтому получаем:

    $$ \int{\frac{3}{5+3x}}\, dx=ln|5+3x|+C=ln(5+3x)+C $$

<< < 234 5 6 > >>