найдите наибольшее значение функции на отрезке - страница 8
Найдите наибольшее и наименьшее значение функции на отрезке:[-1;2] у=2х³+3х²-12х-1
Решение: Найдем производную функции$$ y’=6x²+6x-12 $$
Приравняем производную к нулю. 6x²+6x-12=0
Через дискриминант решаем квадратное уравнение.
D=18²=324
x=1 первый корень уравнения.
x=-1,5 второй корень.
Теперь проверяем, принадлежат ли эти точки заданному промежутку. x=-1,5 не принадлежит. отбрасываем эту точку.
Теперь вычислим значение функции в оставшейся точке x=1 и на концах отрезка, то есть в точках x=-1 и x= 2.
y=2+3-12-1=-8
y=-2+3+12-1=12
y=16+12-24-1=3
получаем максимум в точке x=-1 (y=12)
минимум в точке x=1(y=-8)Найдите наименьшее и наибольшее значение функции на отрезке: а). y=x^3-3x^2+9 x принадлежит [-1;1]
б). у= x^3+3x^2-9 х принадлежит [-1;3]
Решение:Решение на задание а) дано в приложении на стр. 3 и 4.
Задание б) - аналогичноНайдем производную
1) 3x^2-6x
теперь нули производной
3x(x-2)
x=0 x=2 не входит в промежуток
подставляем эти значения в исходную функцию и выбираем наименьшее и наибольшее
y(-1)=-1-3+9=5- наименьшее
y(0)=9 наибольшее
y(1)=1-3+9=7
2) производная равна
3x^2+6x
нуль функции
3x(x+2)=0
x=0 x=-2 не входит в промежуток
y(0)=-9 наименьшее
y(-1)=-1+3-9=-7
y(3)=27+27-9=45 наибольшее

Y=√x-2 Найдите наибольшее и наименьшее значение функции на отрезке [3;11]
Решение: Y(3)=√(3-2)=1наим
y(11)=√(11-2)=3 наиб
У наименьший = 1
у наибольший = 3
так их определяют, но посмотри ещё сам, вот график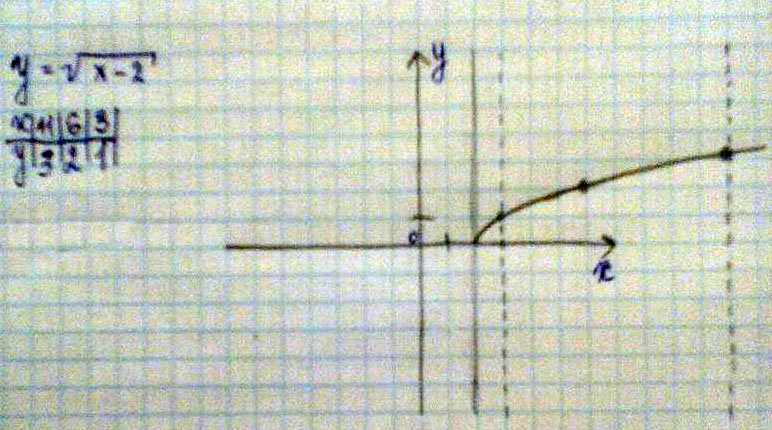
Найдите наименьшее и наибольшее значения линейной функции: В) у = 0,4х:, если х принадлежит (-∞; 0]; Г) у=0,4хесли х принадлежит (-5;5)
Решение:У=0,4х - возрастающая линейная функция
в) при х∈(-∞;0]
у(наименьшее)-не существует
у(наибольшее)=у(0)=0,4*0=0
г) при х∈(-5;5) не существует наибольшего и наименьшего
значения для у, т.к. (-5;5)-открытый интервал
!*** вот если бы х∈[-5;5], то
у(наименьшее)=у(-5)=0,5*(-5)=-2
у(наибольшее)=у(5)=0,4*5=21) Найдите дифференциал функции у=cos^3x ^-это степень 2) Найдите наибольшие и наименьшие значение функции у=6х^3-3х^3-12х+7 на отрезке 1<=x<=2 3) 15-х-2х^2>0 4) у=корень 2-Х^2 х+2 х+1 6) 1/ sin^2 альфа - 1/tg ^2альфа=1
Решение: $$ 1)(cos^3x)’=3cos2^x*(-sin^3x) \\ 2) y’=9x^2-12\\ x=2/\sqrt{3}\\ x=-2/\sqrt{3} \\ f(2/\sqrt{3})=8/3*\sqrt{3}-24/\sqrt{3}+7\\ f(1)=3-12+7=-2\\ f(2)=24-24+7=7 $$наибольшее-f(2)=7
наименьшее -f(1)=-2
3)
2x^2+x-15<0
D=11^2
x_1=-3
x_2=5/2
ответ $$ (-\infty,-3)\cup(5/2,\infty) $$
6)
$$ 1/sin^2a-1/tg^2a=1\\ 1/sin^2a-cos^2a/sin^2a=1\\ 1-cos^2a=sin^2a\\ 1=sin^2a+cos^2a\\ 1=1 $$


