Системы уравнений
- Графический способ решения систем линейных уравнений
Предположим, что в каждом уравнении системы
$$ \begin{cases}a_1x + b_1y = c_1\\a_2x + b_2y = c_2\end{cases} \;\;\;\;(1) $$
хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
a1x + b1y = c1.
Если b1 =/= 0, то уравнение... - Как решать систему уравнений с двумя неизвестными.Система двух линейных уравнений с двумя неизвестными Совместные и несовместные системы Системой двух линейных уравнений с двумя неизвестными называется совокупность уравнений вида $$ \begin{cases}a_1x + b_1y = c_1\\ a_2x + b_2y = c_2\end{cases}\;\;\;(1) $$ где х и у - неизвестные величины, а a1, b1 , c1 и a2, b2 , c2 - некоторые заданные числа. Примером системы двух линейных уравнений с двумя неизвестными может...
- Примеры решений систем уравнений
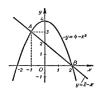Рассмотрим некоторые типичные системы уравнений, решение которых сводится к решению квадратных уравнений.
Пример 1. Решить систему уравнений
$$ \begin{cases}x^2 + 3y^2 -xy-2x+1 = 0\\x-y=1\end{cases} $$
Поскольку второе уравнение этой системы линейно относительно каждой из переменных х и у, то одна из этих переменных,; например у, легко выражается через другую:
у = х - 1.
Подставляя это выражение для у в первое уравнение системы, получаем:
x2...
Предположим, что в каждом уравнении системы
$$ \begin{cases}a_1x + b_1y = c_1\\a_2x + b_2y = c_2\end{cases} \;\;\;\;(1) $$
хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
a1x + b1y = c1.
Если b1 =/= 0, то уравнение...
Рассмотрим некоторые типичные системы уравнений, решение которых сводится к решению квадратных уравнений.
Пример 1. Решить систему уравнений
$$ \begin{cases}x^2 + 3y^2 -xy-2x+1 = 0\\x-y=1\end{cases} $$
Поскольку второе уравнение этой системы линейно относительно каждой из переменных х и у, то одна из этих переменных,; например у, легко выражается через другую:
у = х - 1.
Подставляя это выражение для у в первое уравнение системы, получаем:
x2...Примеры и задачи на системы уравнений
