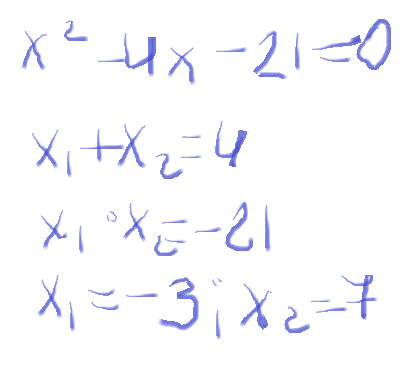решение уравнений »

найдите все корни уравнения - страница 8

  • Найдите корни уравнения: x^2 - 4x - 21 = 0


    Решение: х2-4x-21=0

    Д=16+84=100=10в квадрате.

    x1=4-10/2=-3

    x2=4+10/2=7

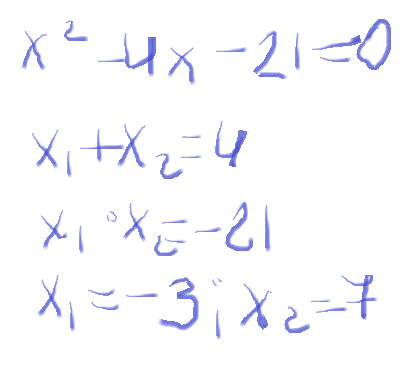
    х - x- Д в квадрате. x - - x...

  • Найдите разность наибольшего и наименьшего корней уравнения: х в четвертой степени -13х в квадрате+36=0


    Решение:

    $$ x^4-13x^2+36=0 \\ t=x^2 \\ t^2-13x+36=0 \\ t_{1}=4 \\ t_{2}=9 \\ x^2=4 \\ x_{1}=-2, x_{2}=2 \\ x^2=9 \\ x_{3}=-3, x_{4}=3 $$

    х=-2 - наименьший корень

    х=3 - наибольший корень

    3-(-2)=3+2=5

    Ответ: 5

    пусть х² - это у

    у²-13у+36=0

    D:169-4*36=25

    у1,2=(13±5)/2

    у1=9

    у2=4

    теперь подставим

    х²=4

    х1,2=±2

    х²=9

    х3,4=±3

    больший корень 3, меньший корень -3

    3-(-3)=6

  • №1 Из множества [1;-1; -2; 3] выделите подмножество,состоящее изь корней уравнения: икс во второй степени минус 6 = х №2 Найдите все целые значения параметра b, при которых уравнение bx=22 имеет целый корень.


    Решение: №1. Подставляем возможные корни в уравнения:
    1^2-6=-5!=1 - не корень
    (-1)^2-6=-5!=-1 - не корень
    (-2)^2-6=4-6=-2 - корень
    3^3-6=9-6=3 - корень
    [-2; 3]

    №2. b должно нацело делить 22, так что b может принимать следующие значения:
    +-1
    +-2
    +-11
    +-22
    (это все делители числа 22, взятые с обоими знаками)

  • 1. Найдите произведение корней уравнения : х кв - 9 = (7+х)(хкв - 5х+6) Ответ: -51 2. найдите среднее арифметическое корней уравнения : (х кв -2х-14)кв = 4(х-1)кв Ответ:1 3. Найдите произведение корней уравнения 256х (в восьмой степени) +1 = 32х (в четвёртой) Ответ: 16


    Решение:

    1) Х^2-9=(7+X)*(X^2-5*X+6)

    Раскроем скобки:

    Х^2-9=7*X^2-7*5*X+7*6+X*X^2-5*X*X+6*X

    Перенесем известные в одну сторону равенства, а НЕизвестные в другую:

    7*X^2-7*5*X+X*X^2-5*X*X+6*X-Х^2=-9-7*6

    7*X^2-7*5*X+X*X^2-5*X*X+6*X-Х^2=-51

    Сокращаем и видим:

    X^3+X^2-29*X=-51

    Произведение корней уравнения равно -51, ну а если надо найти корни уравнения (их в задании нет) - то матрицей элементарно, т.е. Х=3

    2) и 3)

    Так же раскроем скобки и Перенесем известные в одну сторону равенства, а НЕизвестные в другую:

  • Найдите корни уравнения1) 9х(в четвёртой степени)+35х( В квадрате)-4=0
    2) 4х(вЧетвёртой степени)-5х(В Квадрате)+1=0


    Решение: $$ 9x^{4}+35 x^{2} -4=0 \\ x^{2} =t \\ 9 t^{2}+35t-4=0 \\ D=35^{2} -4*9*(-4)=1225+144=1369 \\ \sqrt{D}= 37 \\ t_{1} = \frac{-35+37}{2*9} \\ t_{1} = \frac{1}{9} \\ t_{2}= \frac{-35-37}{2*9} \\ t_{2}=-4 \\ $$

    Корень (-4) не подходит, так как t=x^2, а квадрат числа НЕ МОЖЕТ быть отрицательным

    $$ x^{2} = t_{1} \\ x^{2} = \frac{1}{9} \\ x_{1}=- \sqrt{ \frac{1}{9}} \\ x_{1}=- \frac{1}{3} \\ x_{2}= \sqrt{ \frac{1}{9}} \\ x_{2}= \frac{1}{3} $$

    Ответ: -1/3 и 1/3

    $$ 4x^{4}-5 x^{2} +1=0 \\ x^{2} =t \\ 4 t^{2}+5t+1=0 \\ D=5^{2} -4*1*4=25-16=9 \\ \sqrt{D}= 3 \\ t_{1} = \frac{5+3}{2*4} \\ t_{1} =1 \\ t_{2}= \frac{5-3}{2*4} \\ t_{2}=\frac{1}{4} $$

    Оба корня положительные, а значит оба корня подходят
    $$ x^{2} =1 \\ x_{1}=-1 \\ x_{2}=1 \\ $$ 

    И

    $$ x^{2} = \frac{1}{4} \\ x_{1}=- \frac{1}{2} \\ x_{2}= \frac{1}{2} $$

    Ответ: 1; -1; 1/2; -1/2

<< < 678 9 10 > >>