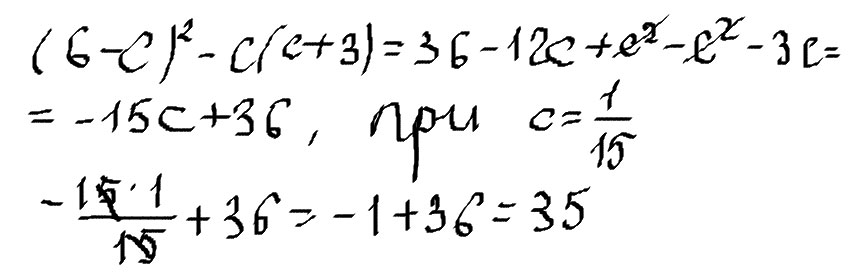упрощение выражений »

упростить выражение и найти его числовое значение - страница 3

  • Решить неравенства a) \( 2^{x} < \frac{1}{2} \)
    b) \( 3^{2x-1} -3^{2x-3} < \frac{8}{3}\)
    c) \( 17 \frac{x}{y-8} \geq 17 \)
    d) \( log_{ 0.2} x < 3 \)
    e) \( log_{ 0.3} ( x^{2} +22) < log_{0.3} 13x \)
    Возвести в степень
    a) \( (\frac{18a ^{9}l ^{3} c ^{8} }{3 x^{4} b ^{4}c ^{4} } ) ^{-3} \)
    b) \(( \frac{7a ^{15}b ^{19}c ^{-24} }{21a ^{1}b ^{-2}c ^{4} } ) ^{ \frac{2}{7} } \)
    Вычислить
    a) $$ \sqrt{x81} * \sqrt{4} + \sqrt{4} \sqrt[3]{343} $$
    b) $$ \sqrt{9+6*1+1} $$
    Упростить выражение
    a) sin(n+t)
    b) \( cos(90^{0} + t)\)
    c) \(tg (\frac{3 \pi }{2} -t ) \)
    d) \( ctg (360^{0} -t ) \)
    Найти основной период функции y=cos 3x
    Найти значение функций
    \( y=2sin(x- \frac{ \pi }{6} ) +1 \) при \( x=\frac{4 \pi }{3} \)
    \( y=cosx x^{2} при x=\pi \)


    Решение: $$ a) 2^x < \frac{1}2\\ 2^x < 2^{-1}\\ x < -1 \\ b) 3^{2x-1}-3^{2x-3} < \frac{8}3\\ 3^{2x}*3^{-1}-3^{2x}*3^{-3} < \frac{8}3\\ t=3^{2x}\\ \frac{1}{3}t-\frac{1}{27}t < \frac{8}{3} \\ \frac{8}{27}t < \frac{8}{3}\\ t < 9\\ 3^{2x} < 9\\ 3^{2x} < 3^2\\ 2x < 2\\ x < 1 $$
    $$ c) 17^{\frac{x}{y-8}}\geq17\\ \frac{x}{y-8}\geq1\\ x\geq y-8 \\ d) log_{0,2}x < 3\\ \frac{log_3x}{log_30,2} < log_327\\ log_3x < log_327*log_30,2\\ log_3x < log_3(27*log_30,2)\\ x < 27log_30,2 \\ e) log_{0,3}(x^2+22) < log_{0,2}13x\\ x^2+22 > 13x\\ x^2-13x+22 > 0\\ x^2-13x+22=0\\ D=(-13)^2-4*1*22=81=9^2\\ x_1=\frac{13+9}{2}=11; \\ x_2=\frac{13-9}{2}=2\\ x\in(-\infty;2)\cup(11;\infty) $$

    $$ a) (\frac{18a^9l^3c^8}{3x^4b^4c^4})^{-3}=\\ =\frac{18^{-3}a^{9*(-3)}l^{3*(-3)}c^{4*(-3)}}{3^{-3}x^{4*(-3)}b^{4*(-3)}}= \\ =\frac{18^{-3}a^{-27}l^{-9}c^{-12}}{3^{-3}x^{-12}b^{-12}}=\\ =\frac{27(xb)^{12}}{18^3(a^9l^3c^4)^3} \\ b) (\frac{7a^{15}b^{19}c^{-24}}{21a^1b^{-2}c^4})^{\frac{2}7}=\\ =(\frac{a^{14}b^{21}c^{-28}}{3})^{\frac{2}7}=\\=3^{-\frac{2}7}a^4b^6c^{-8} $$

    $$ a) \sqrt{x81}*\sqrt{4}+\sqrt{4}\sqrt[3]{343}=9\sqrt{x}*2+2*7=14+18\sqrt{x}\\ b) \sqrt{9+6*1+1}=\sqrt{16}=4 \\b) cos(90^0+t)=-sint \\ c) tg(\frac{3}2\pi-t)=ctgt \\ d) ctg (360^0-t)=-ctgt $$


    y=cos(3x)
    Период функции y=cos(x) T=2π
    cos(x)=cos(x+T)
    cos(3x)=cos(3(x+K))
    3(x+K)=2π
    3x+3K=2π
    x=2/3π

    $$ y=2sin(x-\frac{\pi}{6})+1; \\ x=\frac{4\pi}3\\ y=2sin(\frac{4\pi}3-\frac{\pi}{6})+1=2sin(\frac{14\pi}{12})+1=\\=2sin(\frac{\pi}{6})+1=2*0,5+1=2\\ y=cos(x^2); \\ x=\pi\\ y=cos(\pi^2)=-0,903 $$

  • 1) Упростить выражение: х(в квадрате) - у (в квадрате). 2ху
    2х ху - у(в квадрате) 2) Чему равно значение выражения а(в -4 степ)умножить на а(в -3 степ) а(в -5 степени) при а=1 3 А) -9 Б)_ 1 9 В) 1 9
     Г) 9


    Решение: (x-y)(x+y) умножить 2xy

    _____________________     =      x+y

    2x умножить y(x-y)

    x-y x y умножить xy            x y x умножить y x-y...

  • Упростить выражение: (6-с)во второй степени -с(с+3) и найдите его значение при: С= -1/15(дробью)


    Решение: Ответ: 35                        

    (6-с)во второй степени -с(с+3)=36-12с+с во 2 степени -с во 2 степени - 3с=36-15с

    если с=-1/15,то 36 - 15*(-1/15)=36+1=37

    так как при умножении - на -,получается +...

    Ответ                          -с во второй степени -с с - с с во степени -с во степени - с - с если с - то - - так как при умножении - на - получается ......

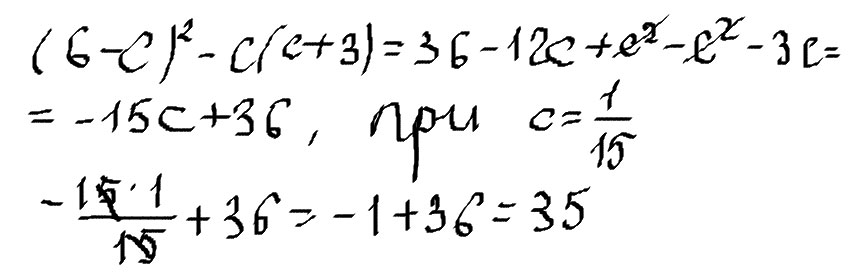
  • 1. Упростить выражение: a) c * c^15 : (c^7)^2 б) -x^3y^2+ 2x^3y^2 - 3x^3y^2 в) (2ab^3)^4 : (2a^2b)^2 г) (n^8)^4 * n : (n^3)^11 2. Вычислить: 10^9 : (2^3)^3 * (5^3)^2 3. Сравнить: (3/4)^8 * (4/3)^7 и (-0.75)^0 4. Сторону квадрата увеличили в 5 раз и площадь нового квадрата стала больше на 384см^2, чем площадь прежнего квадрата. Найти сторону. 5. Уравнение: (25x^3)^2 * (5x^5)^3 : (125x^8)^2 Ps: ^ - степень, * - умножить, / - дробь.


    Решение: 1.
    a    ) c * c^15 : (c^7)^2= c^16/с^14= c^2

     б) -x^3y^2+ 2x^3y^2 - 3x^3y^2= x^3y^2(-1+2-3)
    в) (2ab^3)^4 : (2a^2b)^2=2ab^12/2a^4b^2=a^-3*b^10
    г)(n^8)^4 * n : (n^3)^11= n^32*n / n^33=n^33/n^33=n

    2.  10^9 : (2^3)^3 * (5^3)^2=5^3
    1) 10^9:2^9=5^9*2^9/2^9=5^9 (сократим 2^9)
    2)5^9:5^6=5^3 (вычтем) 

    3.  (3/4)^8 * (4/3)^7 >  (-0.75)^0
    (3/4)^8*(4/3)^7=3^7*4^6
     (-0.75)^0=1

    5. (25x^3)^2 * (5x^5)^3 : (125x^8)^2 = 25x^6*5x^15/125x^16=125x^21/125x^16=125x^5

  • 2) турист, путешествуя на электричке и на теплоходе, преодолел расстояние в 230 км. Скорость электрички была 60 км/ч, а теплохода 25 км/ч . Сколько времени турист проехал на электричке , если на теплоходе он проплыл на 1ч. меньше?

    3) упростить выражение: (x-5y)во второй степени + 10xy


    Решение: Пусть х часов ехал на теплоходе, тогда х+1 часов ехал на электричке. Значит 60*(х+1)км проехал на электричке , 25хкм проехал на теплоходе Т.к. всего проехал 230 км.

    Составим уравнение:60*(х+1)+25х=23060х+60+25х=23085х=170х=2часа ехал на теплоходе 1)2+1=3часа проехал на электричке Ответ:3ч


    3. = х в квадрате - 10ху+ 25у+10ху= х в квадрате + 25у

<< < 123 4 5 > >>