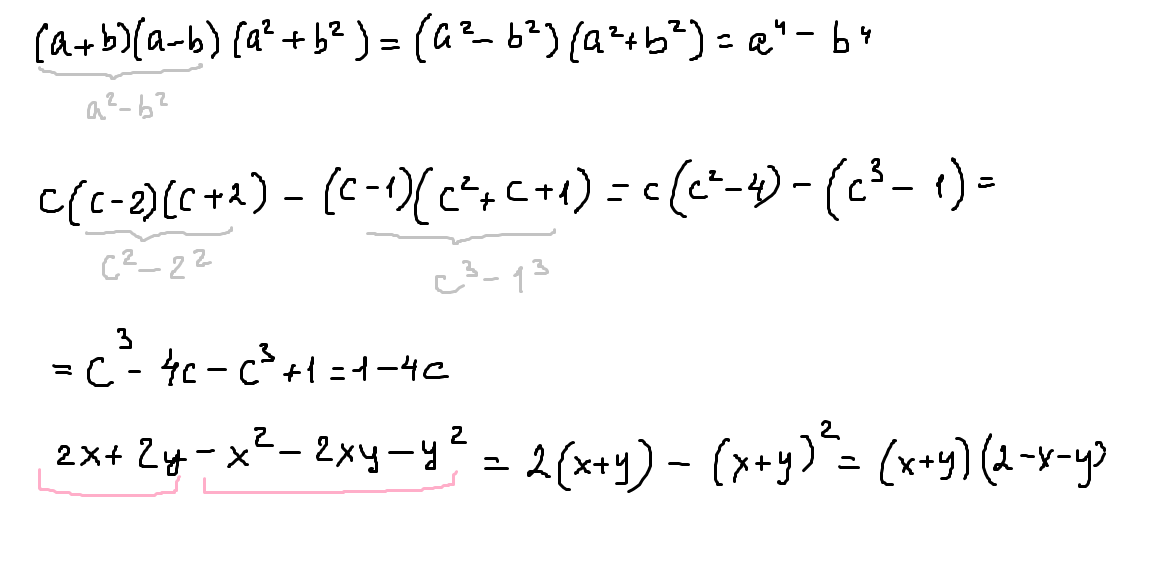упрощение выражений »

упростите выражение - страница 13

  • 10) представьте в виде многочлена (a+b)(a-b)(a^2+b^2)
    11) упростите выражение c(c-2)(c+2)-(c-1)(c^2+c+1)
    12) разложите на множители многочлен 2x+2y-x^2-2xy-y^2


    Решение: 10)
    $$ (a+b)\cdot(a-b)\cdot(a^2+b^2)=(a^2-b^2)\cdot(a^2+b^2)=a^4-b^4 $$
    11)
    $$ c\cdot(c-2)\cdot(c+2)-(c-1)\cdot(c^2+c+1)=\\ =c\cdot(c^2-2^2)-(c-1)\cdot(c^2+c+1)=\\ =c^3-4c-(c^3-1^3)=c^3-4c-c^3+1=1-4c=-4c+1. $$
    12)
    $$ 2x+2y-x^2-2xy-y^2=2(x+y)-(x^2+2xy+y^2)=\\ =2(x+y)-(x+y)^2=(x+y)\cdot(2-(x+y))=(x+y)\cdot(2-x-y). $$

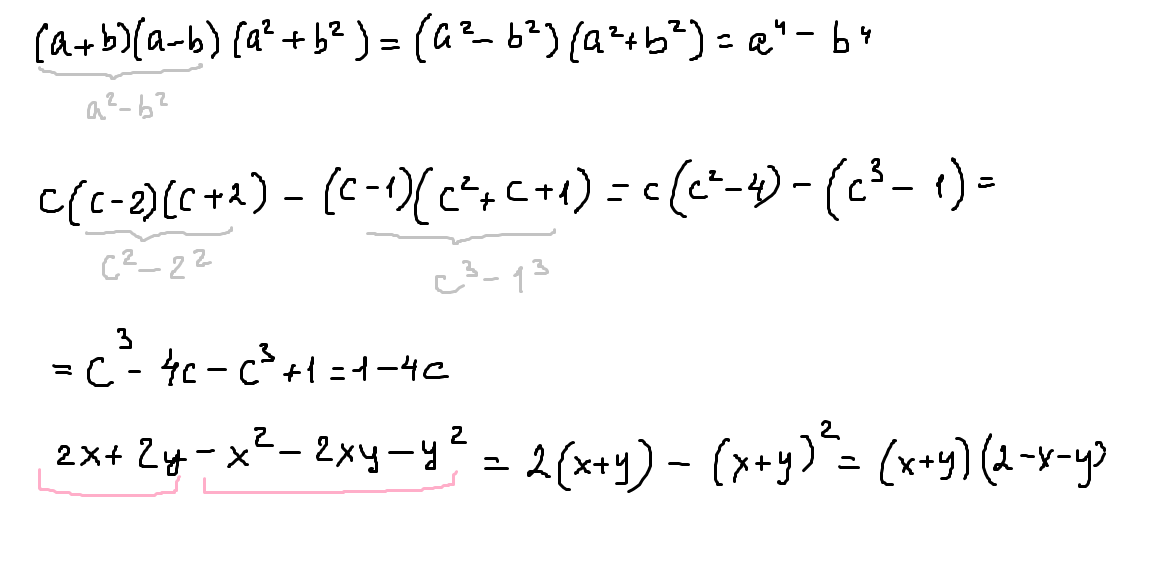
    a b cdot a-b cdot a b a -b cdot a b a -b c cdot c- cdot c - c- cdot c c c cdot c - - c- cdot c c c - c- c - c - c-c - c - c . x y-x - xy-y x y - x xy y x y - x y x y cdot - x...

  • 2. Выполните действия: а) -5ху(3х2 - 0,2у2 + ху); б) (х – 5)(х + 4); в) (35х3у - 28х4) : 7х3 3. Упростите выражение, используя ФСУ: (р + 3)2 - (3р - 1)(3р + 1).
    4. Найти три последовательных натуральных числа, если известно, что квадрат меньшего из них на 47 меньше произведения двух других.
    5. Докажите, что значение выражения не зависит от значения переменной: 2х3 – 2(х - 3)(х2 + 3х + 9)


    Решение: 2. а) -5ху(3х^2 - 0,2у^2 + ху)=-15x^3y+xy^3-5x^2y^2

      б)(х – 5)(х + 4)=x^2+4x-5x-20=x^2-x-20

      в)(35х^3у - 28х^4) : 7х^3=5y - 4x

    3.(р + 3)2 - (3р - 1)(3р + 1=2p+6 -9p^2 - 1=2p-9p^2+5

    5.2х^3 – 2(х - 3)(х^2 + 3х + 9)=x^3-(x-3)*(x^2+3x+9)=x^3-x^3-3x^2-9x+3x^2+9x+27=27

    Этим мы доказали, что результат не зависит от переменной

    4. Первое число - х

      Второе число - х+1

      Третье число - х+2

    Составляем уравнение:

    (x+1)(x+2)-x^2=47 

    x^2+2x+x+2-x^2=47

    3x=45

    x=15 - первое число

    15+1=16 - второе число

    15+2=17 - третье число

    Проверка:16*17-15^2=272-225=47

    . а - ху х - у ху - x y xy - x y   б х х x x- x- x -x-   в х у - х х y - x . р - р - р p - p - p- p . х х - х х x - x- x x x -x - x - x x x Этим мы доказали что результат не...

  • 1. Преобразовать подкоренное выражение к более простому виду, после чего дробь сократить
    5/(1+∛(32cos²15*cos²15-10-8√3)
    2. Выразить tg²α*tg²α+ctg²α*ctg²α через m, где m=tgα+ctgα


    Решение: $$ 1)\; \; \frac{5}{1+\sqrt[3]{32\cdot (cos^215)^2-10-8\sqrt3}}=[\, cos^2 \alpha =\frac{1+cos2 \alpha }{2}\, ]=\\\\=\frac{5}{1+ \sqrt[3]{32\cdot (\frac{1+cos30}{2})^2-10-8\sqrt3} }=\frac{5}{1+\sqrt[3]{\frac{32}{4}\cdot (1+\frac{\sqrt3}{2})^2-10-8\sqrt3}}=\\\\=\frac{5}{1+\sqrt[3]{8\cdot (1+\sqrt3+\frac{3}{4})-10-8\sqrt3}}=\frac{5}{1+\sqrt[3]{8+8\sqrt3+6-10-8\sqrt3}}=\frac{5}{1+\sqrt[3]{4}} \\ 2)\; \; \; tg^2 \alpha +ctg^4 \alpha =?\\\\tg \alpha +ctg \alpha =m\; \; \to \\\\(tg \alpha +ctg \alpha )^2=tg^2 \alpha +2\cdot tg \alpha \cdot ctg \alpha +ctg^2 \alpha =tg^2 \alpha +ctg^2 \alpha +2\cdot 1\\\\m^2=tg^2 \alpha +ctg^2 \alpha +2\; \; \to \; \; tg^2 \alpha +ctg^2 \alpha =m^2-2\\\\(tg^2 \alpha +ctg^2 \alpha )^2=tg^4 \alpha +2\cdot tg^2 \alpha \cdot ctg^2 \alpha +ctg^4 \alpha =tg^4 \alpha +ctg^4 \alpha +2\to \\\\(m^2-2)^2=tg^4 \alpha +ctg^4 \alpha +2\; \; \to \\ tg^4 \alpha +ctg^4 \alpha =(m^2-2)^2-2 \\ tg^4 \alpha +ctg^4 \alpha =m^4-4m^2+4-2=m^4-4m^2+2 $$

  • Выражение 1-tg^2 a / 1+tg^2 a можно преобразовать к виду.


    Решение: $$ \frac{1-tg^2 \, \alpha }{1+tg^2 \, \alpha }=\frac{1 - \frac{\sin^2{ \alpha }}{\cos^2{ \alpha }} }{\frac{1}{\cos^2{ \alpha }}}=\cos^2{ \alpha } \cdot (1 - \frac{\sin^2{ \alpha }}{\cos^2{ \alpha }})= \\\\ =\cos^2{ \alpha } - \sin^2{ \alpha }=\cos{2 \alpha } $$

    $$ \frac{1-tg^{2}a}{1+tg^{2}a} =(1- \frac{sin^{2}a}{cos^{2}a} ):(1+ \frac{sin^{2}a}{cos^{2}a} )=\frac{cos^{2}a-sin^{2}a}{cos^{2}a} :\frac{sin^{2}a+cos^{2}a}{cos^{2}a} = \\ \frac{cos^{2}a-sin^{2}a}{cos^{2}a} * \frac{cos^{2}a}{sin^{2}a+cos^{2}a} =\frac{cos^{2}a-sin^{2}a}{1} * \frac{1}{1} =cos2a \\ $$

  • Преоброзуйте в дробь выражение:
    \( \frac{x}{x-1} + \frac{x}{x+1} \)
    \( \frac{x}{x-2y} - \frac{4y ^{2} }{x ^{2}-2xy } \)
    \( 2a+b - \frac{4ab}{2a+b} \)
    Упростите выражение:
    \( \frac{3}{x+3} + \frac{3}{x^{2}-3x } + \frac{2x}{9-x^{2} } \)
    Заранее благодарство :)


    Решение: $$ \frac{x}{x-1} + \frac{x}{x+1} = \frac{x(x+1)+x(x-1)}{(x-1)(x+1)}= \frac{x^2+x+x^2-x}{x^2-1}= \frac{2x^2}{x^2-1} \\ \frac{x}{x-2y} - \frac{4y ^{2} }{x ^{2}-2xy } = \frac{x^2}{x(x-2y)} - \frac{4y ^{2} }{x(x-2y) } = \frac{x^2-4y^2}{x(x-2y)} = \frac{(x-2y)(x+2y)}{x(x-2y)} = \frac{x+2y}{x} \\ 2a+b - \frac{4ab}{2a+b} =\frac{(2a+b)^2-4ab}{2a+b} =\frac{4a^2+4ab+b^2-4ab}{2a+b} =\frac{4a^2+b^2}{2a+b} \\ \frac{3}{x+3} + \frac{3}{x^{2}-3x } + \frac{2x}{9-x^{2} } = \frac{3}{x+3} + \frac{3}{x(x-3) } - \frac{2x}{(x-3)(x+3) } = \\\ = \frac{3x(x-3)+3(x+3)-2x^2}{x(x+3)(x-3)}= \frac{3x^2-9x+3x+9-2x^2}{x(x+3)(x-3)}= \frac{x^2-6x+9}{x(x+3)(x-3)}= \\\ =\frac{(x-3)^2}{x(x+3)(x-3)}=\frac{x-3}{x(x+3)} $$

<< < 111213 14 15 > >>