неравенства »
решите неравенство - страница 15
Решите неравенство:
/х+14/ - 7* /1 - х/ > х
/ - модуль
Решение: |х+14| - 7* |1 - х| > х
или что тоже самое |х+14| - 7* |x -1| > х
разобьем на три интервала
1) х+14<0 и x-1<0
x<-14 и x<1
объединяя оба эти условия получим x<-14
на этом интервале наше неравенство имеет вид
-(х+14) + 7* (x -1) > х
-x-14+7x-7>x
6x-21>x
5x>21
x>21/5 но это противоречит условию x<-14. На этом интервале решения нет.
2) х+14≥0 и x-1<0
x≥-14 и x<1
объединяя оба эти условия получим -14≤x<1
на этом интервале наше неравенство имеет вид
(х+14) + 7* (x -1) > х
x+14+7x-7>x
8x+7>x
7x>-7
x>-1
объединяя это условие с -14≤x<1 получим -1 <x<1
3) х+14≥0 и x-1≥0
x≥-14 и x≥1
объединяя оба эти условия получим x≥1
на этом интервале наше неравенство имеет вид
(х+14) - 7* (x -1) > х
x+14-7x+7>x
-6x+21>x
21>7x
3>x
объединяя это условие с x≥1 получим 1≤x<3
теперь последнее действие: объединим решения 2) и 3)
-1 <x<3 или x∈(-1;3)
/х+1/+x²+2х+1⩾0
Решите неравенство
/х+1/ эт модуль
Решение: /х+1/+x²+2х+1⩾0 Решите неравенство
пусть /х+1/=t,
заметим, что x²+2х+1=(x+1)²=I (х+1) I ²
тогда
/х+1/+x²+2х+1⩾0 примет вид t+t²≥0 ⇔ t(t+1)≥0
t≥0 t≥0 ⇔ t≥0
/х+1/=t ⇔/х+1/≥0 при x∈(-∞,+∞)
или так.
/х+1/+(x+1)²⩾0 при x∈(-∞,+∞), т. к /х+1/≥0 при x∈(-∞,+∞)
и (x+1)²⩾0 при x∈(-∞,+∞)
Решить неравенство
Х² - /5Х+6/ >0
/модуль/
Решение: $$ x^2-|5x+6|>0 $$
1) если $$ 5x+6 \geq 0\quad \Leftrightarrow\quad x \geq - 1,2 $$
то под модулем выражение не отрицательно, поэтому модуль просто опускаем
$$ x^2-|5x+6|>0\\x^2-5x-6>0\\x_1=6;\quad x_2=-1\\x\in(-\infty;-1)\cup (6;+\infty) $$
с учетом рассматриваемого условия
$$ x\in(-1,2;-1)\cup (6;+\infty) $$
2) если $$ 5x+6 < 0\quad \Leftrightarrow\quad x < - 1,2 $$
тогда под модулем выражение отрицательно, когда раскрываем модуль и меняем знаки
$$ x^2-|5x+6|>0\\x^2+5x+6>0\\x_1=-3;\quad x_2=-2\\x\in(-\infty;-3)\cup (-2;+\infty) $$
с учетом рассматриваемого условия $$ x\in(-\infty;-3)\cup (-2;-1,2) $$Решить неравенство: (x^4+3x^3+4x^2-8)/x^2 < 0;
(x-1)(x-2)(x-3)/(x+1)(x+2)(x+3)>1
Решение: 7.
(x^4+3x^3+4x^2-8)/x^2 < 0
числитель: x^4+3x^3+4x^2-8
корни x1 = 1 x2 = -2
x^4+3x^3+4x^2-8 = (x-1)(x-2)(x^2+2x+8)
знаменатель: x^2 всегда>0
x≠0
тогда имеем:
(x-1)(x+2)(x^2+2x+8)<0
(x^2+2x+8) всегда >0
(x-1)(x+2)<0
x≠-2 x≠1
+ -2 _ 0 _ 1 + x∈]-2;0[∪]0;1[
6.
(x-1)(x-2)(x-3)/(x+1)(x+2)(x+3)>1
(x+1)(x+2)(x+3)/(x-1)(x-2)(x-3) - 1>0
общий знаменатель: (x-1)(x-2)(x-3)
числитель:
(x-1)(x-2)(x-3) -(x+1)(x+2)(x+3) = -(6x^2+8x+6)
-(6x^2+8x+6)/(x-1)(x-2)(x-3)>0
(6x^2+8x+6)/(x-1)(x-2)(x-3) <0
6x^2+8x+6 всегда > 0
(х+1)(х+2)(х+3) < 0
_ -3 + -2 _ -1 +1) решите интеграл \( \int\limits^2_1 {(x^3+2)} \, dx \)
2) Решите неравенство log₀,₁(7x+3)>-1
Решение: 2) неравенство½log₀,₁ ( 3) - 2=log₀,₁(7x+3) zal: 7x+3>0 ⇒7x> -3 ⇒ x> -³/₇ x∈(-³/₇,+∞)
log₀,₁ ( 3)^¹/² - 2=log₀,₁(7x+3) - 2=log₀,₁ 0,1⁻²=log₀,₁ 100
log₀,₁ √3 +log₀,₁ 100=log₀,₁(7x+3)
log₀,₁100√3= log₀,₁(7x+3)
100√3= 7x+3
7x=100√3 -3 /:7
x=100√3 -3 >0
7
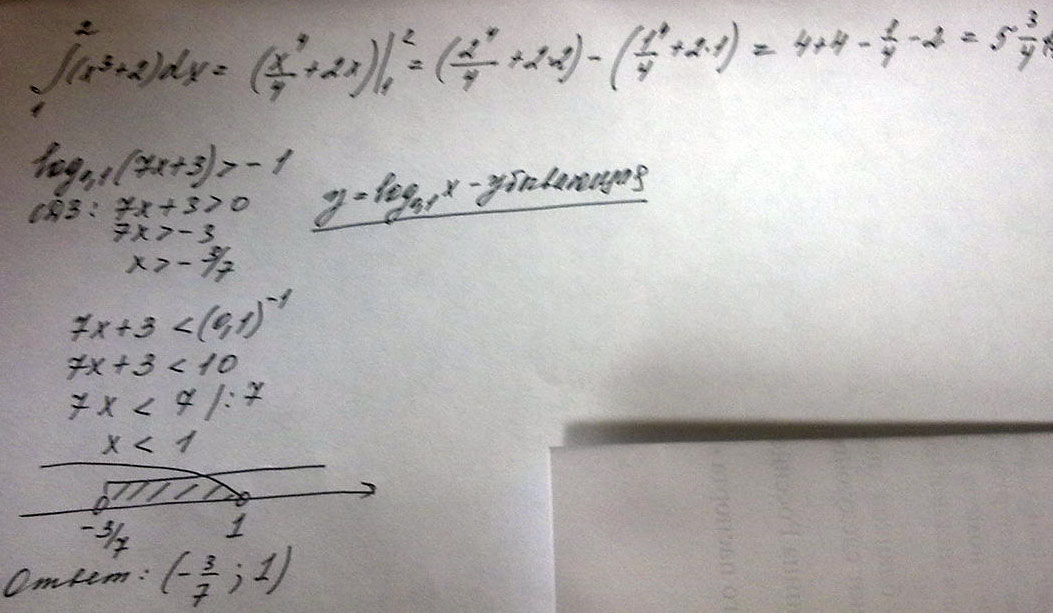

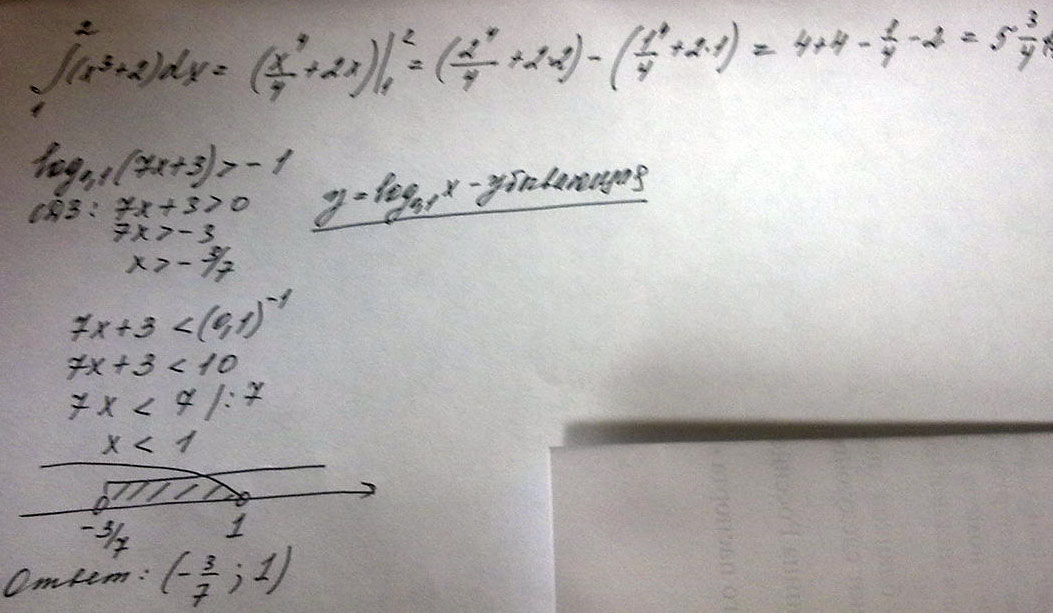
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...