неравенства »
решить логарифмическое неравенство - страница 2
Решите логарифмическое неравенство \(\log_{0,2}^2x \geq 6-\log_{0,2}x\)
Решение: Переносите все в левую часть, вводите новую переменную, решаете квадратное неравенство )$$ \log_{0,2}^2 x \geq 6-\log_{0,2} x, \\ \log_{0,2}^2 x + \log_{0,2} x -6 \geq 0, \\ \log_{0,2} x=a, \\ a^2+a-6 \geq 0, \\ a^2+a-6 = 0, \\ a_1=-3, a_2=2, \\ (a+3)(a-2) \geq 0, \\ \left [ {{a \leq -3} \atop {a \geq 2}} \right. \left [ {{\log_{0,2} x \leq -3,} \atop {\log_{0,2} x \geq 2}} \right. \left [ {{x \geq 0,2^{-3}} \atop {x \leq 0,2^{2}}} \right. \left [ {{x \geq 125} \atop {x \leq 0,04}} \right. \\ x\in(-\infty;0,04]\cup[125;+\infty). $$
Решить логарифмическое неравенство :
Lgx > 1-Lg4
Решение: Lgx>1-lg4
lgx>lg10-lg4
lgx>lg(10/4)
x>10/4
x>2,5
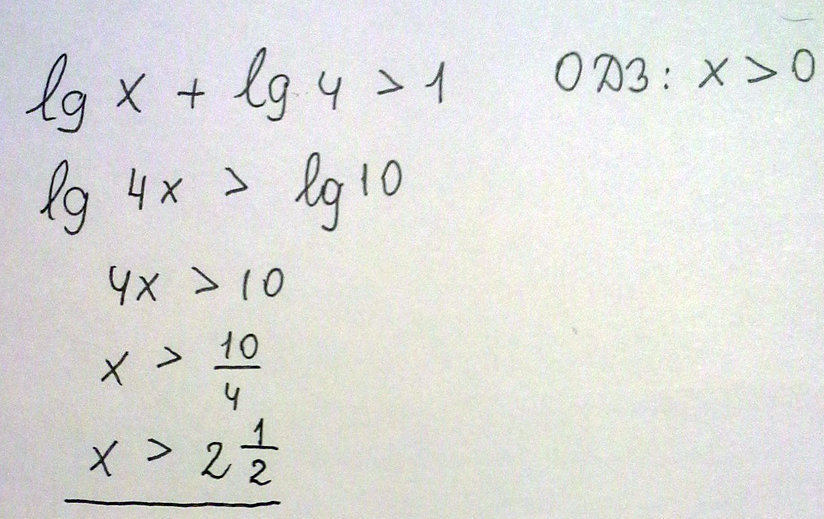
Решите логарифмическое неравенство log1\7(5x+3)≥-1\2
Решение: log1\7(5x+3)≥-1\2
log по основанию к 7^-1 числа (5х+3)≥-1\2
1/(-1) log по основанию к 7 числа (5х+3)≥-1\2
-1 log по основанию к 7 числа (5х+3)≥-1\2
log по основанию к 7 числа (5х+3)^-1 ≥-1\2
(5х+3)^-1 ≥ (1/\(\sqrt{7}\))
1/(5х+3) ≥ (1/\(\sqrt{7}\))
\(\sqrt{7}\) ≥(5х+3)
возв в квадрат, получаем:
7 ≥ 25х^2+30x+9; 25х^2+30x+9-7 \( \leq \)0 ; 25х^2+30x+2 \( \leq\) 0
Решаем методом интервалов и получаем ответРешить логарифмическое неравенство \(\log_x(\log_3 x +\log_{27}x +2) \geq \frac{1}{\log_3 x}\)
Решение: $$ log_x(log_3x+log_{27}x+2) \geq \frac{1}{log_3x} $$
ОДЗ:$$ x > 0; x = 1; \\ log_x(log_3x+ \frac{1}{3} log_{3}x+2) \geq log_x3 \\ log_x(\frac{4}{3} log_{3}x+2) \geq log_x3 \\ \left \{ {{x > 1} \atop {\frac{4}{3} log_{3}x+2 \geq 3}} \right.\Rightarrow \\ \left \{ {{x > 1} \atop {log_{3}x \geq \frac{3}{4} }} \right.\Rightarrow \left \{ {{x > 1} \atop {x \geq 3^{ \frac{3}{4}} }} \right.\Rightarrow \left \{ {{x > 1} \atop {x \geq \sqrt[4]{27} }} \right. \\ \left \{ {{0 < x < 1} \atop {\frac{4}{3} log_{3}x+2\leq3}} \right.\Rightarrow \\ \left \{ {{0 < x < 1} \atop {log_{3}x\leq\frac{3}{4} }} \right.\Rightarrow \left \{ {{0 < x < 1} \atop {x\leq3^{ \frac{3}{4}} }} \right.\Rightarrow \left \{ {{0 < x < 1} \atop {x\leq\sqrt[4]{27} }} \right. $$
Ответ:$$ 0 < x < 1; x \geq \sqrt[4]{27}. $$решите логарифмическое неравенство log2(8-x)<1
Решение: log2(8-x)<1 8-x>08-х<2 x<8
x>8-2
x>6
Ответ: (6;8)
*В прикреплении решение вчерашней контрольной
log2(8-x)<1
log2(8-x)<log2(2)
8-x<2
x>6
C другой стороны
8-x>0
x<8
Объединяя два условия, получим
6<x<8

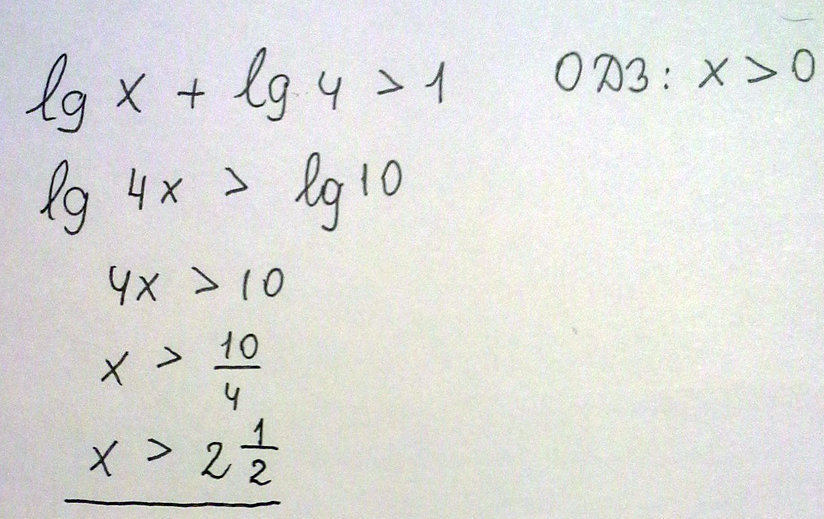
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...