степени »

неравенство степень - страница 6

  • Решить неравенство: \( x^{2} + 3x - 4 < 0 \)


    Решение: $$ x^{2} +3x-4 < 0 \\ x^{2} +3x-4=0 \\ D=9+4*4=9+16=25 \\ \sqrt{D} =5 \\ x_{1} = \frac{-3+5}{2} = \frac{2}{2} =1 \\ x_{2} = \frac{-3-5}{2} =- \frac{8}{2} =-4 \\ \ (x-1)(x+4) < 0 \\ $$
      +  - +
    ----------------|-------------------------|-----------------> x
      -4 1

    $$ x\in (-4;1) $$

    X²+3x-4<0
    x1+x2=-3 U x1*x2=-4
    x1=-4 U x2=1
       +  _  +
    ----------------(-4)-------------------(14)----------------
    x∈(-4;1)

  • Решите неравенство: 3,5 в степени x^2-5x>3,5 в степени -6


    Решение: 3,5 ^(x²-5x)>3,5^(-6)
    3,5>1, возрастает
    x²-5x>-6
    х²-5х+6>0
    х²-5х+6=0
    D=25-24=1
    x1=(5+1)/2=3
    x2=(5-1)/2=2

    Ответ: х∈(-∞;2)U(3;+∞)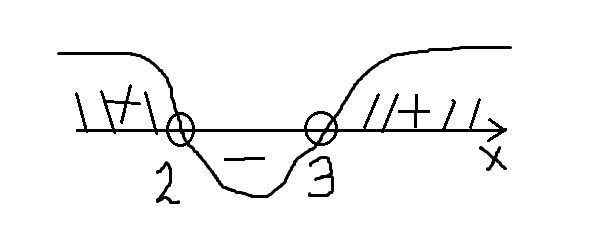
    x - x - возрастаетx - x - х - х х - х D - x x - Ответ х - U...

  • решите неравенство: (1/5)в степени х в квадрате +2х больше (1/25) в степени 16-х


    Решение: приводим к одинаковым основаниям : 5 

    степень в скобках

    5(-Х в квадрате)больше 5(-32+2х)

    теперь приравниваем степени

    -х в квадрате больше -32-2х

    переносим всё в одну сторону получаем 

    -х в квадрате+32-2х больше 0 

    решаем неравенство

    (1/5)^(х² +2х) > (1/25)^(16-х)

             приведём павую часть неравенства к основанию 1/5


    (1/5)^(х² +2х) > (1/5)^2(16-х)

     

    Основание степени 1/5<1, а мы знаем, что показательная ф-ция с основанием меньше 1   - убывающая  = >  значит ф-ция f(x) = 1/5^x    убывающая    = >  


    большему значению ф-ции соответствует меньшее значение аргумента, т.е.

    х² +2х < 2(16-х)

    х² +2х - 32  + 2х < 0

    х² + 4х - 32 < 0


    Исследуем ф-цию f(x) = х² + 4х - 32.  Найдем нули:

    х² + 4х - 32 = 0

    D = 16 + 4*32 = 16 + 128 = 144

    х₁ = (-4 + 12)/2 = 4

    х₂ = (- 4 - 12)/2 = -8

      + - 8 4 +
    ____________о__________________о_______________

      _

    f(x) принимает отрицательные значения на промежутке (4 ; -8)

    Ответ:     (4 ; -8).


  • Решить неравенство: \(\frac{(x+1)^3}{x-3} <0 \)


    Решение: $$ \frac{(x+1)^3}{x-3} <0 $$

    1. Рассмотрим функцию и определим область определения функции

    $$ y=\frac{(x+1)^3}{x-3} \\ x-3 eq 0 \\ x eq 3 \\ D(y)=(-\infty;3)U(3;+\infty) $$

    2. Определяем нули функции

    $$ y=0 \\ \frac{(x+1)^3}{x-3}=0 \\ x+1=0 \\ x=-1 $$

    3. Знаки на промежутки (смотреть во вложения)

    Ответ: $$ (-1;3). $$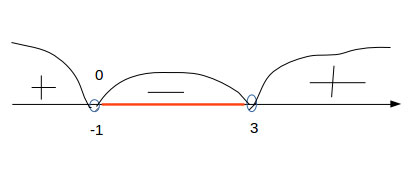 frac x x-...

  • Решить неравенство: (1/3) в степени 5+2x>1/27


    Решение: $$ ( \frac{1}{3})^{5+2x}> \frac{1}{27} \\3^{-(5+2x)}>3^{-3}\\-(5+2x)>-3\\5+2x<3\\2x<3-5\\2x<-2\\x<-1 $$
    От - бесконечности до -1
<< < 456 7 8 > >>