дроби »
приведите дроби к общему знаменателю - страница 2
Приведите дроби к общему знаменателю
/- дробь
1/2+1/4
2/3+1/6
5/8+ 5/24
1/2-1/8
2/3- 4/9
3/4 - 1/12
Решение: 1/2+1/4=2/4+1/4=3/4 2/3+1/6=4/6+1/6=5/6 5/8+5/24=15/24+5/24=20/24=5/6 1/2-1/8=4/8-1/8=3/8 2/3-4/9=6/9-4/9=2/9 3/4-1/12=9/12-1/12=8/12=2/3В 1) НОЗ- 4 домножите 1 число на 2( это уже ответ при сложении будет 3/4)
2) 6 домножите 1 число на 2(5/6)
3) 24 домножите1 число на 3(20/24 сократите на 2 и будет 10\12 и ещё на 2 5\6)
4)8 домножь 1 число на 4 (3\8)
5)9 домножите 1ь число на 3(2/9)
6)12 домножите 1 число на 4(11/12)Приведите дроби к общему знаменатель и решите их: 2/7+2/3 1/2+1/3 4/5+1/2 2/3+3/10
Решение: Вот решение всё легко
2/7+2/3=2/*3+2*7(общий знаменатель 21) 6+14=20/21
1/2+1/3=(общий знаменатель 6) 1*3+1*2=5/6
4/5+1/2+(10)4*2+1*5=13/10
2/3+3/10=(30)2*10+3*3=29/30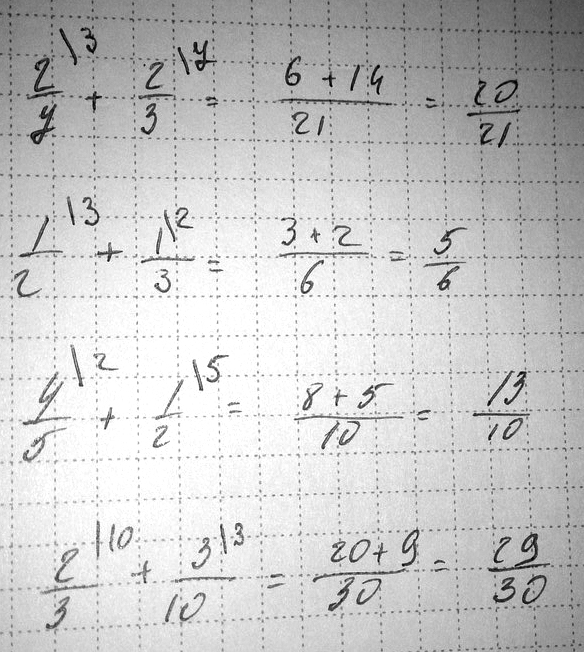
Приведите дроби к общему знаменателю
и) 1/70 и 1/60 к)1/50 и 1/80 л) 1/60 и 1/15 м) 1/24 и 1/120
Решение: и) 1/70 и 1/60
Общий знаменатель равен 420.
Домножаем первую дробь на 6, вторую на 7.
6/420 и 7/420.
к)1/50 и 1/80
Общий знаменатель равен 400.
Домножаем первую дробь на 8, вторую на 5.
8/400 и 5/400.
л) 1/60 и 1/15
Общий знаменатель равен 60.
Домножаем вторую дробь на 4.
1/60 и 4/60.
м) 1/24 и 1/120
Общий знаменатель равен 120.
Домножаем первую дробь на 5.
5/120 и 1/120.Приведите дроби к общему знаменателю и найдите разность:
а) 5/6 и 2/3; б) 5/6 и 7/12; в) 11/15 и 2/3; г) 40/60 и 9/15; д) 2/3 и 1/8; е)17/42 и 6/21; ж) 2/8 и 4/24 ; з) 23/45 и 4/15 ;
Решение: 2
a) 5/6-2/3=5/6-4/6=1/6
3
б)5/6-7/2=5/6-21/6=-16/6=-8/3=-2 2/3
5
в)11/15-2/3=11/15-10/15=1/15
4
г)40/60-9/15=10/15-9/15=1/15
8 3
д)2/3-1/8=16/24-3/24=13/24
2
e)17/42-6/21=17/42-12/42=5/42
3
ж)2/8-4/24=6/24-4/24=2/24=1/12
3
з)23/45-4/15=23/45-12/45=11/45 цифры над дробями означают на сколько нужно умножить дробь, чтобы уравнять знаменатели. и только в примере д) нужно разделить дробь.Приведите дроби к общему знаменателю:
1) 2x/y⁴ и 3/y 2) 2b/a⁵ и 6/y 3) 2/3xy² и 7/6x²y 4) 4/x+5 и 3/7x 5) a/2a+2 и 3/a+1 6) 2x/3x-3y и 3y/4x+4y
Решение: $$ 1) \frac{2x}{y^{4}}, \frac{3y^{3}}{y^{4}} \\ 2) \frac{2by}{a^{5}y}, \frac{6a^{5}}{a^{5}y} \\ 3) \frac{4x}{6x^{2}y^{2}}, \frac{7y}{6x^{2}y^{2}} \\ 4) \frac{28x}{7x(x+5)},\frac{3(x+5)}{7x(x+5)}=\frac{3x+15}{7x^{2}+35x} \\ 5) \frac{a}{2(a+1)},\frac{6}{2(a+1)} \\ 6) \frac{2x*(4x+4y)}{3(x-y)4(x+y)}= \frac{8x^{2}+8xy}{12(x^{2}-y^{2})}=\frac{8x^{2}+8xy}{12x^{2}-12y^{2}}, \\ \frac{3y*(3x-3y)}{3(x-y)4(x+y)}= \frac{9xy-9y^{2}}{12(x^{2}-y^{2})}=\frac{9xy-9y^{2}}{12x^{2}-12y^{2}} $$.
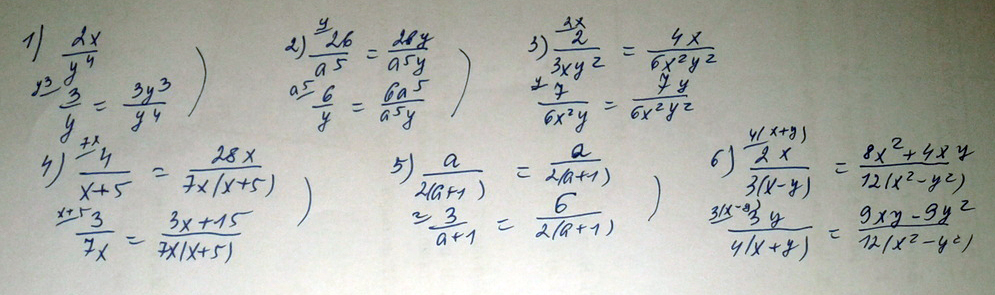

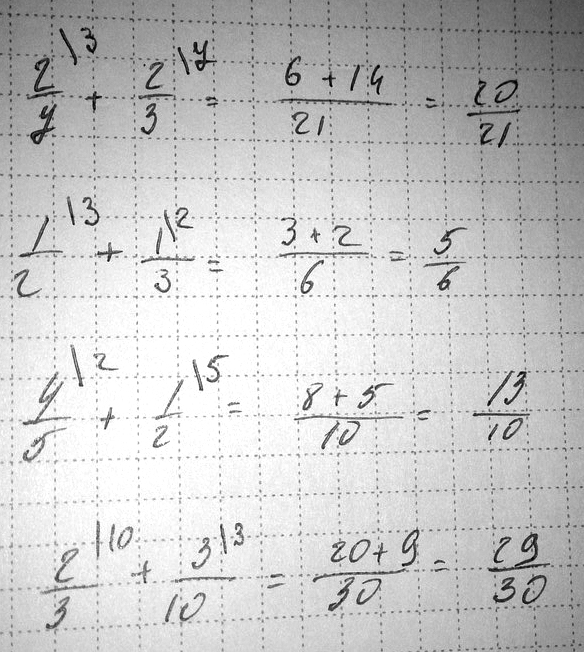
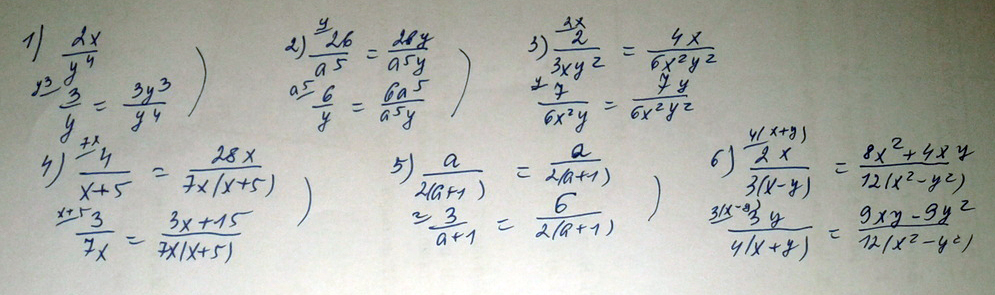
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...