обыкновенные дроби - страница 2
Cоставить кроссворд на тему "натуральные числа и обыкновенные дроби"
Решение: По горизонтали: 1. Деление числителя и знаменателя на одно и то же число.2. Сотая часть числа. 3. Дробь, у которой числитель и знаменатель, взаимно простые числа. 4. Для нахождения общего знаменателя надо находить НОД или НОК? 5. Для сокращения дроби нужно находить НОД или НОК?
По вертикали: 6. Частное двух чисел. 7. Действие, при помощи которого находится дробь от числа. 8. Название дроби, у которой числитель больше или равен знаменателю.
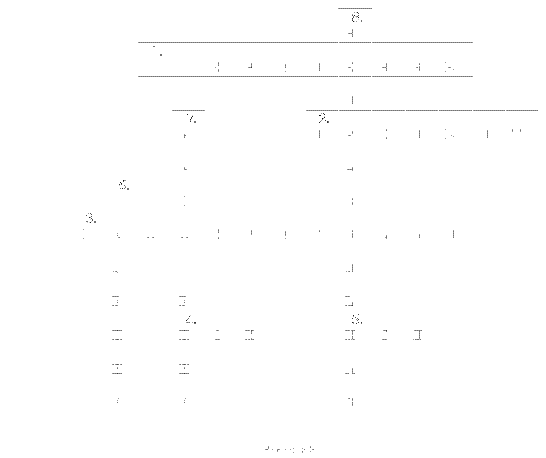
Среди чисел 1/218; 0; 1,514; 7целых2/5; 93; 8,01; 89/100; 2; 2целых9/11 найди: а) натуральные числа; б) обыкновенные дроби; в) смешанные числа; г) десятичные дроби.
Решение: А) 93 2Б) 1/218
В) 1,514 7целых2/5 8,01 2целых9/11
Г) 89/100
вроде так, если только у вас все дроби с десятичным покзателем не относятся к смешанным.
Тогда под буквой в оставите только 7целых2/5 и 2целых9/11, а остальной перенесете в букву г
а) 93; 2 - натуральные числа;
б) 1/218; 89/100 - обыкновенные дроби;
в) 7 2/5; 2 9/11 - смешанные числа;
г) 1,514; 8,01 - десятичные дроби
Представьте в виде неправильной обыкновенной дроби смешанные числа: 3 3/4; 5 7/10; 14 4/5; 8 7/12; 24 3/4; 15 3/7; 9 9/11; 14 20/21; 12 3/23; 15 5/24.
Решение: 1) 3 3/4 = 3+3*4/4 = 15/42) 5 7/10 = 7+5*10/10 = 57/10
3) 14 4/5 = 4+14*5/5 = 74/5
4) 8 7/12 = 7+8*12/12 = 103/12
5) 24 3/4 = 3+24*4/4 = 99/4
6) 15 3/7 = 3+5*7/7 = 108/7
7) 9 9/11 = 9+9*11/11 = 108/11
8) 14 20/21 = 20+14*21/21 = 314/21
9) 12 3/23 = 3+12*23/23 = 279/23
10) 15 5/24 = 5+15*24/24 = 365/24
1) 15/3
2) 57/10
3) 74/5
4) 103/12
5) 99/4
6) 108/7
7) 108/11
8) 314/21
9) 279/23
10) 365/24Представьте в виде неправильной обыкновеной дроби смешанные числа
11 целых 9 11
12 целых 7 12
13 целых 11 13
14 целых 3 14
15 целых 8 15
16 целых 13 16
Решение: 130/11
151/12
180/13
199/14
233/15
269/16
Как выполнять такие задания :
1) Умножь знаменатель на целое число
2) К произведению прибавь числитель дроби, получил новый числитель
3) А знаменатель остаётся прежним.
Например, первое задание:
Знаменатель 11 умножаете на целое число 11, получаете 121.
Прибавляете к 121 числитель 9, получаете 130 - это новый числитель.
А знаменатель остаётся прежним - 11
Получается неправильная обыкновенная дробь: 130/111)11целых9/11 =130/11
2)12целых7/12=151/12
3)13целых11/13=180/13
4)14целых3/14=199/14
5)15целых8/15=233/15
6)16целых13/16=269/16Обыкновенные дроби, сложение и вычитание смешанных чисел.
1. Веревку длиной 256 м разрезали на две части, она из которых в 7 раз длиннее второй. На сколько метров одна часть веревки длиннее второй?
2. В археологических раскопках участвовали две экспедиции. В первой было в три раза больше сотрудников, чем во второй. Когда во вторую экспедицию прибыли ещё 18 человек, то в двух экспедициях стало 66 сотрудников. Сколько стало сотрудников во второй экспедиции?
Решение: №1
Пусть одна часть х м, а другая 7х м Решим уравнение
х+7х=256
8х=256
х=256:8
х=32
32м один из кусков
32*7=224 м другой
№2
Пусть х сотрудников было во 2 группе, тогда в первой 3х. Решим уравнение
3х+х+18=66
4х=66-18
4х=48
х=48:4
х=12 чел во 2 группе
12*3=36 чел в первой
12+18=30 чел стало во 2 группе

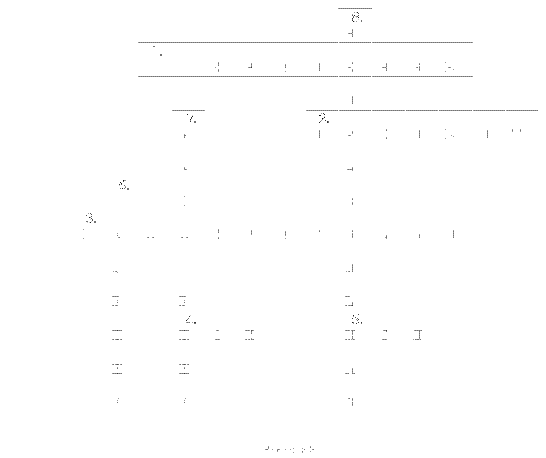
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...